当前位置：首页 > news >正文

CRC校验码的检错性能（三）——基于对偶码重量分布计算漏检概率

news 来源：原创 2025/5/23 8:55:03

CRC（Cyclic Redundancy Check，循环冗余校验），是一种数字编码技术，广泛应用于数字通信的传输差错检测，或数字存储的数据完整性检测，最早由W. Wesley Peterson于1961年发表的论文《Cyclic Codes for Error Detection》中提出。

事实上，对于差错检测而言，几乎不太可能做到检出所有（100%）的错误，意即检测手段给出“无错”结论时，这一结论本身很难做到100%的置信度。因此，人们评价一种检错手段的性能时，通常真正关心的是“错误已经发生，但未能发现”的概率（本文称之为漏检概率Pud，Probability of Undetected Error），显然，这个概率越小越好！

本文在充分理解CRC校验码及其对偶码生成矩阵原理的基础之上，手工计算出CRC-4/SAE J2716的对偶码在码字长度\(n=16\)时的重量分布，引用Koopman教授公布的该校验码对应的原码重量分布数据，并利用Wolfram的在线计算工具完成了MacWilliams恒等式的验算。

MacWilliams恒等式揭示了线性分组码的原码和对偶码重量分布之间的关系，本文详细推导了基于CRC校验码之对偶码重量分布计算其漏检概率的公式。进一步分析了\( 0^{0} \)在数学上的争议性定义对漏检概率计算的影响，并通过对公式的简单变换而规避该影响。

最后，本文分别基于原码和对偶码的重量分布，完成了CRC-4/SAE J2716在码字长度n = 16，\( 10^{-6} \sim 0.5 \)误比特范围内的漏检概率计算。计算结果表明，在低误比特率条件下，基于对偶码重量分布计算CRC校验码漏检概率时，对计算的数值精度有着较高的要求。

1. CRC校验码及其对偶码

CRC校验码是一种二进制线性分组码，信息位长度\( k \)，校验位长度\( r \)，码字长度\( n=k+r \) 的CRC校验码，可通过一个\( r \)次的生成多项式\( G(x)=g_{r}x^{r}+\cdots +g_{1}x^{1}+g_{0}x^{0} \)构造，选定\( G(x) \)后，该线性分组码的典型生成矩阵\( G \)亦随之确定：

典型生成矩阵是一个\( k \)行\( n \)列的矩阵，每一行都是独立的（不可由其它任意行的线性组合获得），可用于构造该线性分组码的\( 2^{k}-1 \)个非0码字。

每个线性分组码\( C(n,k) \)都有唯一一个与之对应的对偶码\( C^{\perp }(n,n-k) \)，对偶码的信息位长度为\( r \)，校验位长度为\( k \)，码字长度为\( n=k+r \)，码字集合中共\( 2^{r} \)个合法码字。对偶码的典型生成矩阵\( G^{\perp } \)可由原CRC校验码的典型生成矩阵\( G \)变换获得（如下图所示）：

在典型生成矩阵\( G \)的\( k \)行\( r \)列校验位矩阵下方添加一个\( r \)行\( r \)列的单位矩阵，构成一个\( n \)行\( r \)列的矩阵\( H \)；
将矩阵\( H \)顺时针旋转90°即为对偶码的典型生成矩阵\( G^{\perp } \)。

以CRC-4/SAE J2716 SENT为例，其生成多项式\( G(x)=x^{4}+x^{3}+x^{2}+1 \)，校验位长度\( r=4 \) ，信息位长度\( k=12 \)时，码字长度\( n=16 \)，其典型生成矩阵如下图：

该CRC-4校验码之对偶码的典型生成矩阵、15个非0码字、各码字的汉明重量（标注于码字右侧），如下图：

可知该CRC-4校验码之对偶码的16个合法码字以及它们汉明重量：

1个汉明重量为 0 的码字：0x0000；
2个汉明重量为 6 的码字：0x8A34、0xC468；
4个汉明重量为 7 的码字：0x268D、0x1D1A、0x68D1、0x5346；
2个汉明重量为 8 的码字：0x4E5C、0xB1A3；
4个汉明重量为 9 的码字：0xACB9、0xE2E5、0x972E、0xD972；
2个汉明重量为10的码字：0x3B97、0x75CB；
1个汉明重量为16的码字：0xFFFF。

2. 麦克威廉姆斯（MacWilliams，马克威伦）恒等式

设\( A_i \)是二进制线性分组码\( C(n,k) \)的\( 2^k \)个有效码字集合中重量为\( i \)的码字数目（数量），则集合\( A=\left \{ A_0,A_1,\cdots ,A_n \right \} \)称为该分组码的重量分布。也可以把码\( C \)的重量分布写成多项式形式：

\[ A(x)=A_0x^0+A_1x^1+ \cdots + A_nx^n =\sum_{i=0}^{n}A_ix^i \]

称\( A(x) \)是二进制线性分组码\( C(n,k,d) \)的重量估值算子（简称重量算子），或称为重量枚举多项式。令\( C^{\perp }(n,n-k,d') \)为码\( C \)之对偶码，则\( C^{\perp } \)的\( 2^{n-k} \)个有效码字集合的重量枚举多项式\( B(x) \)可写为：

\[ B(x)=B_0x^0+B_1x^1+ \cdots + B_nx^n =\sum_{i=0}^{n}B_ix^i \]

二进制线性分组码\( C \)及其对偶码\( C^{\perp} \)的码字重量分布有这样一些性质：

零重（全0）码字的数量恒为一，即\( A_0=B_0 \equiv 1 \)；
全重（全1）码字的数量为0或1，即\( A_n=0或1 \)，\( B_n=0或1 \)；
全重（全1）码字的数量为1（\( A_n=1 \)）时，重量分布是对称的，即\( A_i=A_{n-i},0 \leqslant i \leqslant n \)，
码重数目之和等于码字总数，即\( \sum_{i=0}^{n}A_i=2^k \)，\( \sum_{i=0}^{n}B_i=2^{n-k} \)；
码字重量或全是偶数，或者奇、偶重量的码字数目相等；
线性分组码的码字重量全为偶数时，其对偶码有（且只有）一个全1码字；线性分组码奇、偶重量的码字数目相等时，其对偶码无全1码字；
线性分组码有（且只有）一个全1码字时，其对偶码的码字重量全为偶数；线性分组码无全1码字时，其对偶码奇、偶重量的码字数目相等；

线性分组码及其对偶码的重量枚举多项式\( A(x) \)与\( B(x) \)之间有一个重要的恒等式——MacWilliams恒等式（注：式中的计算基于整数域而非GF(2)域）：

\[ \begin{aligned}
A(x)&=\sum_{i=0}^{n}A_ix^i= \frac{1}{2^{n-k}} (1+x)^{n} \sum_{i=0}^{n}B_i(\frac{1-x}{1+x})^i = \frac{1}{2^{n-k}} \sum_{i=0}^{n}B_i(1-x)^i(1+x)^{n-i} \\ \\
B(x)&= \sum_{i=0}^{n}B_ix^i= \frac{1}{2^k} (1+x)^{n} \sum_{i=0}^{n}A_i(\frac{1-x}{1+x})^i = \frac{1}{2^k} \sum_{i=0}^{n}A_i(1-x)^i(1+x)^{n-i}
\end{aligned} \]

MacWilliams恒等式的重要价值在于，为了计算一个\( (n,k) \)二进制线性码的重量枚举多项式，通常需要了解所有\( 2^k \)个码字的重量。显然这是一项艰巨的任务，除非\( k \)的取值相对较小。但是如果\( k \)的值非常大而\( (n-k) \)的值很小，就可以先计算其对偶码\( C^{\perp } \)的重量枚举多项式，由此再计算出\( C \)的重量枚举多项式。

以CRC-4/SAE J2716 SENT为例，其生成多项式\( G(x)=x^{4}+x^{3}+x^{2}+1 \)，校验位长度\( r=4 \) ，信息位长度\( k=12 \)时，码字长度\( n=16 \)，直接计算该CRC校验码的重量分布需要枚举4096个码字的重量\(^{[7]}\)（本文通过查询Philip Koopman的网站数据获得），而其对偶码（仅16个码字）的重量分布可手工计算或利用EXCEL编制简单的工具完成。该CRC校验码原码\(^{[7]}\)及其对偶码的重量分布如下表：

i	Ai	Bi	i	Ai	Bi
0	1	1	9	0	4
1	0	0	10	1017	2
2	11	0	11	0	0
3	0	0	12	219	0
4	233	0	13	0	0
5	0	0	14	17	0
6	1003	2	15	0	0
7	0	4	16	0	1
8	1595	2

依据上表分别写出此CRC校验码及其对偶码的重量枚举多项式：

\[ \begin{aligned}
A(x)&=17x^{14}+219x^{12}+1017x^{10}+1595x^{8}+1003x^{6}+233x^{4}+11x^{2}+1x^{0} \\
B(x)&= 1x^{16}+2x^{10}+4x^{9}+2x^{8}+4x^{7}+2x^{6}+1x^{0}
\end{aligned} \]

利用MacWilliams恒等式基于\( B(x) \)求\( A(x) \)的验证，有：

\[ A(x) = \frac{1}{16}[(1+x)^{16}+2(1+x)^{10}(1-x)^6+4(1+x)^{9}(1-x)^7+2(1+x)^{8}(1-x)^8+4(1+x)^{7}(1-x)^9+2(1+x)^{6}(1-x)^{10}+(1-x)^{16}] \]

上式基于手工计算过于繁琐，本文将其输入Wolfram网站的在线计算工具验证，结果正确，如下图：

利用MacWilliams恒等式基于\( A(x) \)求\( B(x) \)的验证，有：

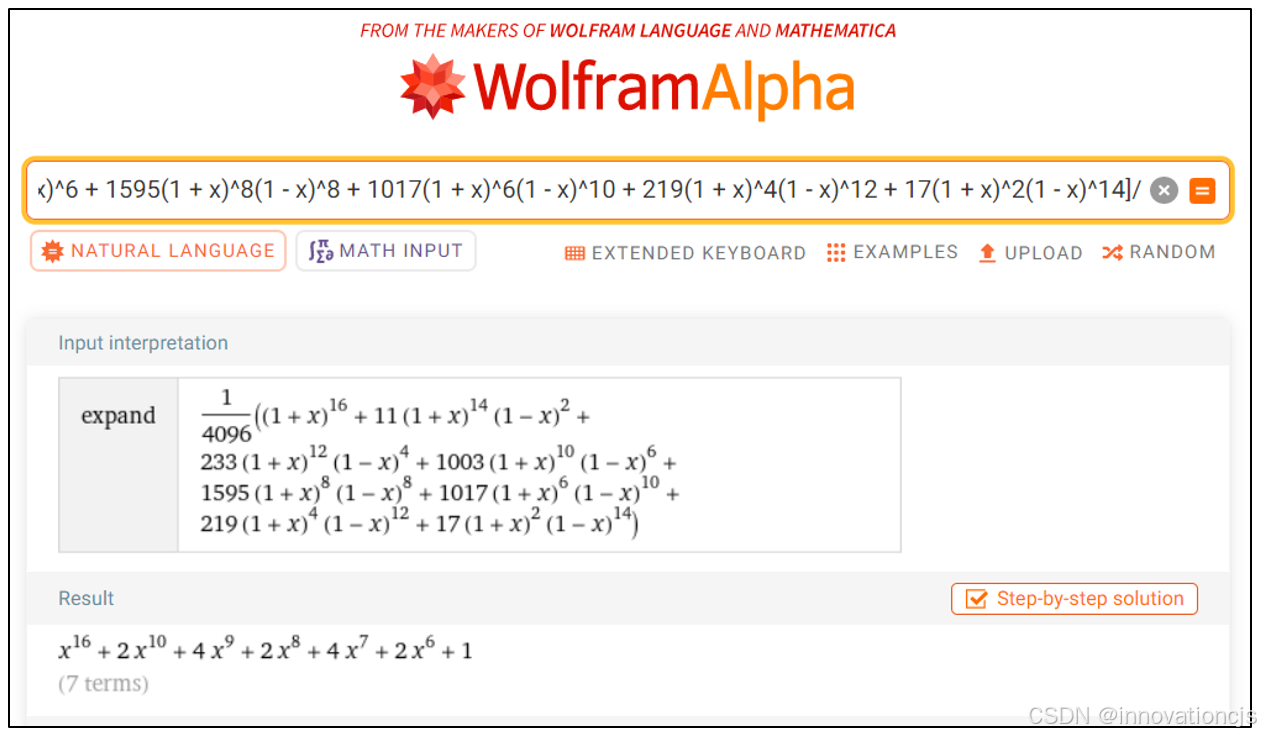
\[ B(x) = \frac{1}{4096}[(1+x)^{16}+11(1+x)^{14}(1-x)^2+233(1+x)^{12}(1-x)^4+1003(1+x)^{10}(1-x)^6+1595(1+x)^{8}(1-x)^8+1017(1+x)^{6}(1-x)^{10}+219(1+x)^4(1-x)^{12}+17(1+x)^2(1-x)^{14}] \]

将上式输入Wolfram网站的在线计算工具验证，结果正确，如下图：

备注：本文不是对MacWilliams恒等式的证明！本文仅是通过实际操作来理解MacWilliams恒等式。

3. 基于对偶码重量分布的CRC校验码漏检概率计算公式

从前文可以看到，即便是对于12个信息位，4个校验位这样极小规模的CRC-4校验码，欲知其漏检概率，我们至少需要完成以下计算：

依据生成多项式及CRC校验码计算方法，计算出该码组的4096个合法码字；
计算出4096个码字的汉明重量，枚举出不同汉明重量值的数量；
计算出每组汉明重量在给定误比特率下对应的概率；
汉明重量≥1的概率之和即为本组CRC校验码在给定的误比特率下的漏检概率。

上述计算没有原理（或理解）上的难度，就是计算量特别大，几乎只能通过编制特定的计算机程序才能完成。而随着信息位长度的增加，很快（比如100-bits）令得计算机穷举法也成为一个理论，不再具备实际操作的可能。

我们已经知道，32位及以下的CRC校验码，通过计算机穷举计算其对偶码的重量分布 B 是具备工程实操性的。自然可以想到利用MacWilliams恒等式计算该CRC校验码的重量分布 A，从而计算出它的漏检概率\( P_{ud} \)。事实上，我们可以基于对偶码的重量分布，利用下式直接计算这个CRC校验码的漏检概率：

\[ P_{ud}=\left [ \frac{1}{2^r} \sum_{i=0}^{n}B_i(1-2p)^i \right ] - (1-p)^n
=\left [ \frac{1}{2^r} \sum_{i=1}^{n}B_i(1-2p)^i \right ] + 2^{-r} - (1-p)^n \]

证明过程如下，已知CRC校验码在误比特率\(p\)的BSC信道下，其漏检概率的计算公式为：

\[ \begin{aligned}
P_{ud} &= \sum_{i=1}^{n}A_i p^i (1-p)^{n-i} \\
&= \left [ \sum_{i=0}^{n}A_i p^i (1-p)^{n-i} \right ] - (1-p)^n \\
&= \left [ (1-p)^n \sum_{i=0}^{n}A_i (\frac{p}{1-p})^i \right ] - (1-p)^n
\end{aligned} \]

令\( x=\frac{p}{1-p} \)，则\( \frac{1-x}{1+x}=1-2p \)，\( 1+x=\frac{1}{1-p} \)，代入MacWilliams恒等式，有：

\[ \begin{aligned}
\sum_{i=0}^{n}A_ix^i &= \frac{1}{2^r}(1+x)^n\sum_{i=0}^{n}B_i(\frac{1-x}{1+x})^i \\
\sum_{i=0}^{n}A_i(\frac{p}{1-p})^i &= \frac{1}{2^r} (\frac{1}{1-p})^n \sum_{i=0}^{n}B_i(1-2p)^i
\end{aligned} \]

将换元后的MacWilliams恒等式代入\( P_{ud} \) 的计算式，可得到基于对偶码的重量分布计算原CRC校验码漏检概率的公式：

\[ \begin{aligned}
P_{ud} &= (1-p)^n\left [ \frac{1}{2^r}(\frac{1}{1-p})^n\sum_{i=0}^{n}B_i(1-2p)^i \right ] - (1-p)^n \\
&= \left [ \frac{1}{2^r}\sum_{i=0}^{n}B_i(1-2p)^i \right ] - (1-p)^n
\end{aligned} \]

若将CRC校验码漏检概率的两种计算方法写为一个计算式，有：

\[ P_{ud} = \sum_{i=1}^{n}A_ip^i(1-p)^{n-i}
= \left [ \frac{1}{2^r}\sum_{i=0}^{n}B_i(1-2p)^i \right ] - (1-p)^n \]

上式须在\( p\in [0,1] \)区间内均有意义：

1) \( p=0 \)时，表明无比特错误，因无错误发生，自然漏检概率\( P_{ud}=0 \)，且错误图样集合有且仅有一个代表无错的全0码字，有\( A_i=0, i>0 \)，

\[ P_{ud}=\sum_{i=1}^{n}A_ip^i(1-p)^{n-i}
=\sum_{i=1}^{n}0\times 0^i \times 1^{n-i} \equiv 0 \]

\[或\]

\[ P_{ud}= \left [ \frac{1}{2^r}\sum_{i=0}^{n}B_i(1-2p)^i \right ] - (1-p)^n
= \left [ \frac{1}{2^r}\sum_{i=0}^{n}B_i \times 1^i \right ] - 1^n
= \frac{1}{2^r} \times 2^r - 1 \equiv 0 \]

2) \( p=1 \)时，表明每个比特都是错误的，错误图样集合有且仅有一个全1码字，有\( A_i=0, i<n \)。当全1码字是本码组有效码字时，\(A_n=1\)，仅有的一个错误图样不能检出，漏检概率\( P_{ud}=1 \)，且对偶码全为偶重码字；当全1码字是本码组无效码字时，\(A_n=0\)，仅有的一个错误图样全部检出，漏检概率\( P_{ud}=0 \) ，且对偶码的偶重码字和奇重码字数量相等。

\[ P_{ud}=\sum_{i=1}^{n}A_ip^i(1-p)^{n-i}
=\sum_{i=1}^{n-1}0\times 1^i \times 0^{n-i} + A_n \times 1^n \times 0^0 =\left\{\begin{matrix}
1, 当 A_n=1 & \\
0, 当 A_n=0 &
\end{matrix}\right. \]

\[或\]

\[ P_{ud}= \left [ \frac{1}{2^r}\sum_{i=0}^{n}B_i(1-2p)^i \right ] - (1-p)^n
= \left [ \frac{1}{2^r}\sum_{i=0}^{n}B_i \times (-1)^i \right ] - 0^n
= \left\{\begin{matrix}
1, & 当B_i全为偶数时 \\
0, & 当B_i奇偶数量相等时
\end{matrix}\right. \]

3) \( p=1-p=0.5 \)时，\( P_{ud} = 2^{-(n-k)} - 2^{-n} = 2^{-r} - 2^{-n} \)。

\[ P_{ud}=\sum_{i=1}^{n}A_ip^i(1-p)^{n-i}
= \sum_{i=1}^{n}A_i (\frac{1}{2})^i (\frac{1}{2})^{n-i}
= (\frac{1}{2})^n\sum_{i=1}^{n}A_i
= (\frac{1}{2})^n(2^k-1)
= 2^{-(n-k)} - 2^{-n} \]

\[或\]

\[ \begin{aligned} P_{ud} &= \left [ \frac{1}{2^r}\sum_{i=0}^{n}B_i(1-2p)^i \right ] - (1-p)^n
             = \left [ \frac{1}{2^r}\sum_{i=0}^{n}B_i \times 0^i \right ] - (\frac{1}{2})^n
             = \frac{1}{2^r} (B_0 \times 0^0 + \sum_{i=1}^{n}B_i \times 0^i) - 2^{-n} \\
           & = 2^{-r} \times 0^0 - 2^{-n}
             = 2^{-r} - 2^{-n} \end{aligned} \]

从\( p\in [0,1] \)全概率区间的讨论来看， CRC校验码漏检概率\( P_{ud} \)的两种计算方法，都存在须将\( 0^0 \)定义为1的计算问题，而\( 0^0 \)的定义在不同应用领域是有争议的，不同软件（或编程语言）也可能有不同的定义，如下图所示（右图为EXCEL的定义）：

为避免\( 0^0 \)可能导致的程序计算错误，可将漏检概率的计算式改写为：

\[ \begin{aligned}
P_{ud} &= \left [ \sum_{i=1}^{n-1}A_i p^i (1-p)^{n-i} \right ] + A_n p^n \\
&= \left [ \frac{1}{2^r} \sum_{i=1}^{n}B_i (1-2p)^i \right ] + 2^{-r} - (1-p)^n
\end{aligned} \]

4. 计算示例

以CRC-4/SAE J2716 SENT为例，其生成多项式\( G(x)=x^{4}+x^{3}+x^{2}+1 \)，校验位长度\( r=4 \)，信息位长度\( k=12 \)，码字长度\( n=16 \)时，分别用两种方法计算该CRC校验码的漏检概率。从前文已知该校验码及其对偶码的重量枚举多项如下：

\[ \begin{aligned}
A(x)&=17x^{14}+219x^{12}+1017x^{10}+1595x^{8}+1003x^{6}+233x^{4}+11x^{2}+1x^{0} \\
B(x)&= 1x^{16}+2x^{10}+4x^{9}+2x^{8}+4x^{7}+2x^{6}+1x^{0}
\end{aligned} \]

设信道的误比特率为\(p\)，漏检概率如下计算：

\[ \begin{aligned}
P_{ud_1}&=17p^{14}(1-p)^{2}+219p^{12}(1-p)^{4}+1017p^{10}(1-p)^{6}+1595p^{8}(1-p)^{8}+1003p^{6}(1-p)^{10} \\
&+233p^{4}(1-p)^{12}+11p^{2}(1-p)^{14}+1p^{0}(1-p)^{16} \\ \\
P_{ud_2}&= 2^{-4} \times [(1-2p)^{16}+2(1-2p)^{10}+4(1-2p)^{9}+2(1-2p)^{8}+4(1-2p)^{7}+2(1-2p)^{6}] + 2^{-4} - (1-p)^{16}
\end{aligned} \]

例如，\( p=10^{-6} \)时，计算可得漏检概率\( \approx 1.1\times 10^{-11} \)，更多的计算结果如下表：

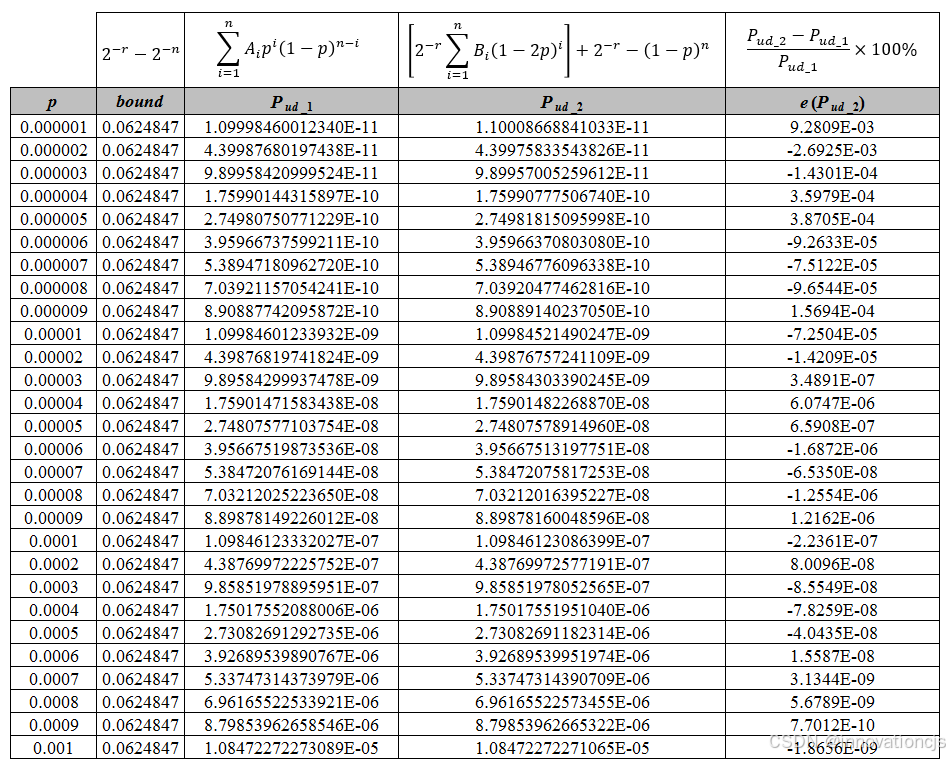
值得注意的是，上表通过EXCEL计算获得。可以看到，两种方法计算的漏检概率并不完全相等，有着一个微小的偏差（见表格第5列）。两种计算方法的计算公式本身是精确的，二者计算结果的偏差由EXCEL的数值计算精度导致\(^{[8]}\)，原理上来说，基于CRC校验码重量分布计算所得的\( P_{ud-1} \)在数值上的精度相对更高。

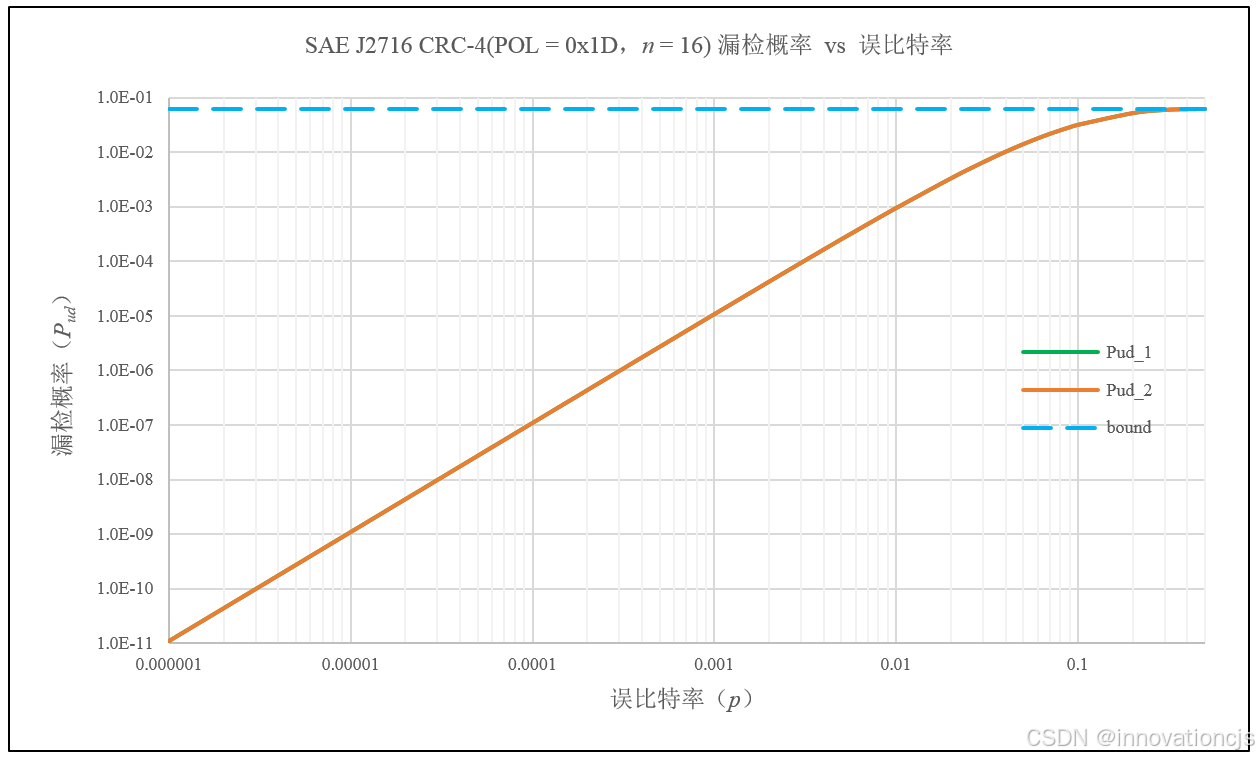
一般地，绘制本计算示例在\( 10^{-6}\sim0.5 \)误比特范围内，漏检概率曲线如下图：