【LeetCode Solutions】LeetCode 141 ~ 145 题解

LeetCode 141. 环形链表（简单）

【题目描述】

给你一个链表的头节点 head，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递。仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true。否则，返回 false。

【示例 1】

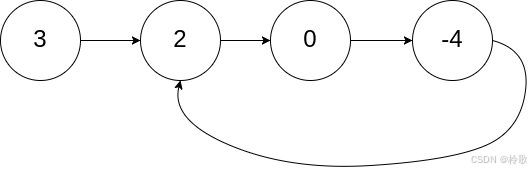
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

【示例 2】

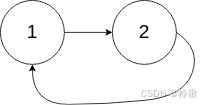
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

【示例 3】

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

【提示】

链表中节点的数目范围是 $[0,10^4]$
$-10^5<=Node.val<=10^5$
pos 为 -1 或者链表中的一个有效索引

进阶：你能用 $O(1)$ 的空间复杂度解决此问题吗？

---

【分析】

最直观的思路就是遍历链表的同时用一个哈希表记录下遍历过的点，如果再次遍历到已经遍历过的点说明存在环。

题目要求使用常数级的空间解决，其中一种思路是可以将遍历过的点 next 指针指向自身，当遍历到某个节点其 next 指向的是自身说明存在环。

还有一种思路是使用快慢指针，快指针每次走两步，慢指针每次走一步，当两个指针能够相遇说明存在环。

---

【代码】

【修改 next 指针】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode* p = head;
        while (p) {
            if (p->next == p) return true;
            ListNode* q = p->next;
            p->next = p;
            p = q;
        }
        return false;
    }
};

【快慢指针】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode *fast = head, *slow = head;
        while (fast && slow) {
            slow = slow->next, fast = fast->next;
            if (fast) fast = fast->next;
            if (fast && fast == slow) return true;  // 快慢指针相等且不为空说明存在环
        }
        return false;
    }
};

LeetCode 142. 环形链表 II（中等）

【题目描述】

给定一个链表的头节点 head，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改链表。

【示例 1】

输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

【示例 2】

输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

【示例 3】

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

【提示】

链表中节点的数目范围在范围 $[0,10^4]$ 内
$-10^5<=Node.val<=10^5$
pos 的值为 -1 或者链表中的一个有效索引

进阶：你能用 $O(1)$ 的空间复杂度解决此问题吗？

---

【分析】

首先和上题一样，用快慢指针进行遍历，如果存在环这两个指针必定会相遇，设相遇点为 $k$，起点为 $a$，环的入口为 $b$。

设起点到环入口的距离 dis[a, b] = x，环入口到相遇点的距离 dis[b, k] = y，假设我们让快慢指针同时回溯，如果慢指针从 $k$ 倒退 $y$ 步就到了环入口，此时快指针倒退 $2y$ 步到环的某个点，我们记为 $k^{\prime }$，那么显然 dis[k', b] = dis[b, k] = y。

又由于慢指针从起点走到环入口时走了 $x$ 步，快指针此时总共走了 $2x$ 步，也就是相当于从 $b$ 又走了 $x$ 步走到了 $k^{\prime }$，即 dis[b, k'] = x。

因为 $k^{\prime }$ 到 $b$ 的距离与 $b$ 到 $k$ 的距离都是 $y$，同时将 $k$ 和 $b$ 倒退 $y$ 步后就分别变成了 $b$ 和 $k^{\prime }$，因此 dis[k, b] = dis[k - y, b - y] = dis[b, k'] = x，这就说明从 $k$ 向前走 $x$ 步就到了环入口 $b$。

接下来如何知道 $x$ 是多少？我们让一个指针从 $a$ 开始走，然后另一个指针从 $k$ 开始走，每次两个指针各走一步，$a$ 和 $k$ 走 $x$ 步都会走到 $b$，因此如果两个点相遇了就说明走到 $b$ 了。

觉得太绕可以画个图跟着模拟一遍。

---

【代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode *fast = head, *slow = head;
        while (fast) {
            fast = fast->next, slow = slow->next;
            if (fast) fast = fast->next;
            if (fast && fast == slow) {
                slow = head;  // 让 slow 回到起点
                while (fast != slow) fast = fast->next, slow = slow->next;
                return slow;
            }
        }
        return nullptr;
    }
};

LeetCode 143. 重排链表（中等）

【题目描述】

给定一个单链表 L 的头节点 head，单链表 $L$ 表示为：$L_0\to L_1\to \dots \to L_{n-1}\to L_n$

请将其重新排列后变为：

$L_0\to L_n\to L_1\to L_{n-1}\to L_2\to L_{n-2}\to \dots$

不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

【示例 1】

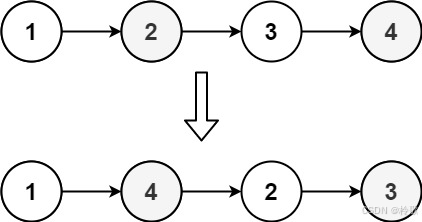
输入：head = [1,2,3,4]
输出：[1,4,2,3]

【示例 2】

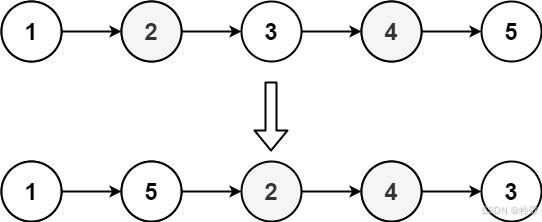
输入：head = [1,2,3,4,5]
输出：[1,5,2,4,3]

【提示】

链表的长度范围为 $[1,5\ast 10^4]$
$1<=node.val<=1000$

---

【分析】

可以先将后半段链表的指针反转（反转方式类似 ），然后用两个指针分别从起点和终点开始分别向右和向左走，边走边交错取节点，这样就能构建出最后交错的链表。

设链表长度为 $n$，如果链表长度为偶数，则后半段链表的起始点为第 $n/2+1$ 或 $(n+1)/2+1$ 个节点，如果长度为奇数，可以让左边链表更长，则后半段链表的起始点为第 $(n+1)/2+1$ 个点，因此我们统一用 $(n+1)/2+1$ 计算。

设后半段链表的起始点为第 $k$ 个节点，那么首先将节点 $k-1$ 与 $k$ 的 next 置为空，然后将节点 $k\sim n$ 反转。接着用两个指针分别从第 1 个节点与第 $n$ 个节点开始遍历，由于后半段长度小于等于前半段，因此后半段链表的指针遍历到空指针时说明修改完成。

---

【代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    void reorderList(ListNode* head) {
        int n = 0;
        for (ListNode* p = head; p; p = p->next) n++;
        ListNode* a = head, *b;
        for (int i = 0; i < (n + 1) / 2 - 1; i++) a = a->next;  // 第 i 个节点只需要从起点跳 i - 1 次
        b = a->next, a->next = nullptr, a = b;  // a 是后半段链表第一个节点的前一个节点，将其 next 置为空
        if (a) b = a->next;  // 后半段节点不为空才需要反转
        while (a && b) {  // 交换完成后 a 就是链表的末尾节点
            ListNode *c = b->next;
            if (a->next == b) a->next = nullptr;  // 第一次交换时先把后半段的第一个节点的 next 置为空
            b->next = a;
            a = b, b = c;
        }
        for (ListNode* p = head; a;) {
            b = a->next;  // 先记下来 a->next
            a->next = p->next;
            p->next = a;
            p = p->next->next, a = b;
        }
    }
};

LeetCode 144. 二叉树的前序遍历（简单）

【题目描述】

给你二叉树的根节点 root，返回它节点值的前序遍历。

【示例 1】

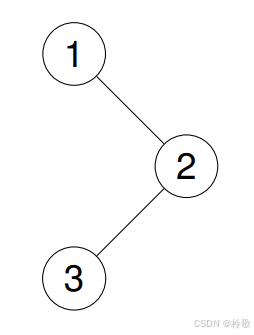
输入：root = [1,null,2,3]
输出：[1,2,3]

【示例 2】

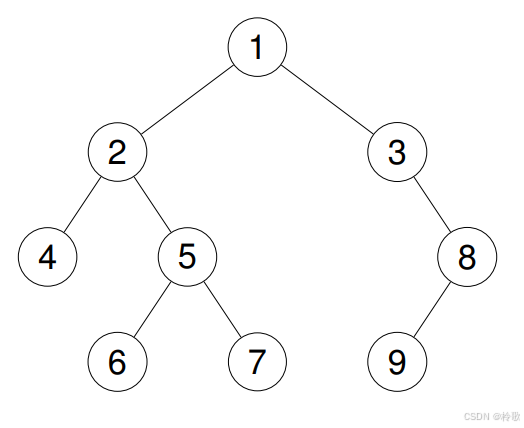
输入：root = [1,2,3,4,5,null,8,null,null,6,7,9]
输出：[1,2,4,5,6,7,3,8,9]

【示例 3】

输入：root = []
输出：[]

【示例 4】

输入：root = [1]
输出：[1]

【提示】

树中节点数目在范围 $[0,100]$ 内
$-100<=Node.val<=100$

进阶：递归算法很简单，你可以通过迭代算法完成吗？

---

【分析】

类似 LeetCode 94.，递归写法很简单就不讲了，主要讲一下迭代算法，前序遍历的迭代写起来比中序遍历简单。

中序遍历是先遍历完左子树再遍历根节点，前序遍历是先遍历根节点，因此从根节点开始入栈，每次节点出栈的同时就可以遍历了，然后入栈的顺序是先入栈右儿子再入栈左儿子，因为根节点遍历完要保证左子树都在右子树之前进行遍历，因此先入栈右子树优先级就会比左子树更低。

---

【代码】

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> stk;
        if (root) stk.push(root);
        while (stk.size()) {
            TreeNode* t = stk.top(); stk.pop();
            res.push_back(t->val);
            if (t->right) stk.push(t->right);
            if (t->left) stk.push(t->left);
        }
        return res;
    }
};

LeetCode 145. 二叉树的后序遍历（简单）

【题目描述】

给你一棵二叉树的根节点 root，返回其节点值的后序遍历 。

【示例 1】

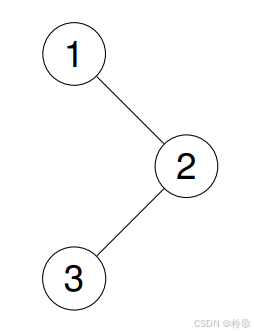
输入：root = [1,null,2,3]
输出：[3,2,1]

【示例 2】

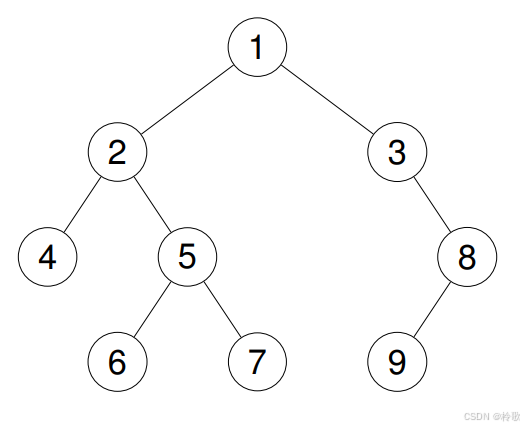
输入：root = [1,2,3,4,5,null,8,null,null,6,7,9]
输出：[4,6,7,5,2,9,8,3,1]

【示例 3】

输入：root = []
输出：[]

【示例 4】

输入：root = [1]
输出：[1]

【提示】

树中节点的数目在范围 $[0,100]$ 内
$-100<=Node.val<=100$

进阶：递归算法很简单，你可以通过迭代算法完成吗？

---

【分析】

后序遍历和前/中序遍历又不太一样，如果直接参考前/中序遍历的方法去想就比较复杂。

前序遍历的顺序为：根 → 左 → 右，后序遍历的顺序为：左 → 右 → 根，那么如果用前序遍历的方式遍历出来这种顺序：根 → 右 → 左，然后将其翻转一下，那就是后序遍历的结果。这样就好实现多了，只需要调转一下上一题中遍历左右子树的顺序即可。

---

【代码】

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> stk;
        if (root) stk.push(root);
        while (stk.size()) {
            TreeNode* t = stk.top(); stk.pop();
            res.push_back(t->val);
            if (t->left) stk.push(t->left);
            if (t->right) stk.push(t->right);
        }
        reverse(res.begin(), res.end());
        return res;
    }
};