当前位置： 首页 > news >正文

前馈控制与反馈控制融合算法详解及python案例分析

news 2025/7/18 16:24:03

目录

  • 前馈控制与反馈控制融合
    • 一、引言
    • 二、前馈控制与反馈控制的基本理论
      • 1. 前馈控制
      • 2. 反馈控制
      • 3. 融合控制的原理
    • 三、融合控制策略的理论推导与分析
      • 1. 理论推导
      • 2. 优势与局限性
    • 四、典型案例分析
      • 案例一：一维动态系统控制
        • 案例描述
        • 分析
      • 案例二：温度控制系统
        • 案例描述
        • 分析
      • 案例三：机器人轨迹跟踪控制
        • 案例描述
        • 分析
    • 五、实战案例：基于 PyQt6 的 GUI 演示
      • 1. GUI 功能需求
      • 2. Python 代码实现
    • 六、结语

前馈控制与反馈控制融合

一、引言

在自动化与控制系统领域，前馈控制和反馈控制分别代表了控制方法中的两大基本思想。传统的反馈控制依靠系统输出与期望值的偏差进行校正，确保系统在扰动下仍能稳定运行；而前馈控制则通过对扰动或参考信号的预先测量或估计，提前进行补偿，从而提高控制系统的响应速度与鲁棒性。二者各有优势，但单独应用时也存在局限性。因此，将两者有机融合便成为提高系统性能、兼顾快速响应与稳健性的有效手段。

本篇博客将详细介绍前馈控制与反馈控制的基本原理、融合方法及其在工程应用中的优势；同时，我们将列举三个典型案例，包括动态系统控制、温度调节和机器人轨迹控制，通过公式推导和仿真实例，深入探讨两种控制策略的互补性。最后，我们将展示一份基于 PyQt6 模块开发的 GUI 程序，提供直观的交互式操作界面，并包含帮助按钮以便用户随时获取相关说明。

在这里插入图片描述

二、前馈控制与反馈控制的基本理论

1. 前馈控制

前馈控制（Feedforward Control）是一种预测性控制方法，其主要思想在于利用参考信号或扰动信息提前进行补偿。假设系统参考输入为 r ( t ) r(t) r(t)，前馈控制器设计目标为根据 r ( t ) r(t) r(t) 生成一个控制量：
u f f ( t ) = f ( r ( t ) ) u_{ff}(t) = f(r(t)) uff​(t)=f(r(t))
其中，函数 f ( ⋅ ) f(\cdot) f(⋅) 根据系统动态或扰动特性来设计。前馈控制不依赖于系统的实际输出 y ( t ) y(t) y(t)，因此具有响应速度快、延迟低的优点。但由于其对模型精度依赖较大，系统参数变化或未知扰动时容易出现误差。

2. 反馈控制

反馈控制（Feedback Control）则是基于误差信号 e ( t ) = r ( t ) − y ( t ) e(t)=r(t)-y(t) e(t)=r(t)−y(t) 进行校正，其基本控制律可以表达为：
u f b ( t ) = K ⋅ e ( t ) u_{fb}(t)=K \cdot e(t) ufb​(t)=K⋅e(t)
其中， K K K 为控制增益（可能为 PID、LQR 或其他形式的控制器参数）。反馈控制的优点在于能够自动校正模型不确定性和外部扰动，但由于存在测量延迟，系统响应速度较前馈控制略慢，且在大扰动下可能会引入震荡。

3. 融合控制的原理

前馈与反馈控制各有优劣，将二者融合能在大部分应用中实现优势互补。融合后的控制律通常写成：
u ( t ) = u f f ( t ) + u f b ( t ) u(t)=u_{ff}(t)+u_{fb}(t) u(t)=uff​(t)+ufb​(t)
也即，系统在预先补偿基础上，再利用反馈机制校正残余误差。这样不仅可以缩短系统响应时间，还能有效抑制由于模型不准确或扰动引起的误差。

在此系统结构中，前馈模块根据参考输入 r ( t ) r(t) r(t) 生成预补偿信号，而反馈模块根据实时测量误差对控制信号进行校正。两者信号合成后作用于系统，实现高精度与高响应的控制目标。

三、融合控制策略的理论推导与分析

1. 理论推导

考虑一个简单的线性系统，其动态可以描述为：
x ˙ ( t ) = A x ( t ) + B u ( t ) \dot{x}(t)=Ax(t)+Bu(t) x˙(t)=Ax(t)+Bu(t)
输出为：
y ( t ) = C x ( t ) y(t)=Cx(t) y(t)=Cx(t)
假设参考输入 r ( t ) r(t) r(t) 希望系统能够跟踪，则设计前馈控制器得到预估控制量 u f f ( t ) u_{ff}(t) uff​(t)，而反馈控制器根据误差 e ( t ) = r ( t ) − y ( t ) e(t)=r(t)-y(t) e(t)=r(t)−y(t) 生成反馈控制量 u f b ( t ) u_{fb}(t) ufb​(t)。整体控制律为：
u ( t ) = u f f ( t ) + u f b ( t ) = f ( r ( t ) ) + K [ r ( t ) − y ( t ) ] u(t)=u_{ff}(t)+u_{fb}(t)=f(r(t)) + K\left[r(t)-y(t)\right] u(t)=uff​(t)+ufb​(t)=f(r(t))+K[r(t)−y(t)]

如果系统满足某些条件（例如系统具有相对零点可控性），则可以通过适当选择函数 f ( ⋅ ) f(\cdot) f(⋅) 和反馈增益 K K K 实现完美的跟踪和稳定性。此时可以引入状态空间的方法，通过极点配置或者最优控制方法进一步优化控制性能。

2. 优势与局限性

融合控制策略相较于单一控制方法具有以下优势：

  • 快速响应： 前馈控制能够根据参考信号提前调整控制量，大大缩短系统响应延迟。
  • 鲁棒性： 反馈控制部分能够实时修正由于模型误差或外部扰动引起的偏差，提高系统稳定性。
  • 灵活性： 结合设计可以适应多种工况，满足不同场景下的性能要求。

然而，其局限性也不容忽视：

  • 模型依赖性： 前馈控制依赖于系统模型的精确性，模型不准时可能导致误补偿。
  • 设计复杂度： 融合设计需要在两部分间找到平衡，设计和调试工作量较大。
  • 实现成本： 对硬件和计算资源有更高要求，特别是在实时控制系统中。

四、典型案例分析

为了更直观地展示前馈与反馈控制融合在实际工程中的应用，下面给出三个典型案例，并对各案例的控制原理进行详细说明。

案例一：一维动态系统控制

案例描述

考虑一简单的一维动态系统，其状态方程为：
x ˙ ( t ) = − a x ( t ) + b u ( t ) \dot{x}(t)=-ax(t)+bu(t) x˙(t)=−ax(t)+bu(t)
目标是使得系统状态 x ( t ) x(t) x(t) 跟踪给定参考信号 r ( t ) r(t) r(t)。利用前馈控制预测参考输入带来的影响，同时利用反馈控制实时校正系统输出，整体控制律为：
u ( t ) = 1 b ( a r ( t ) + r ˙ ( t ) ) + K [ r ( t ) − x ( t ) ] u(t)=\frac{1}{b}\left(ar(t)+\dot{r}(t)\right)+K\left[r(t)-x(t)\right] u(t)=b1​(ar(t)+r˙(t))+K[r(t)−x(t)]

分析
  • 前馈部分： 根据参考信号 r ( t ) r(t) r(t) 及其变化率 r ˙ ( t ) \dot{r}(t) r˙(t) 计算预期的控制量。
  • 反馈部分： 根据误差 r ( t ) − x ( t ) r(t)-x(t) r(t)−x(t) 进行实时修正，提高系统跟踪精度。

这种设计既可以提前补偿系统动态，又能保证对模型误差和外部扰动有良好的鲁棒性。

案例二：温度控制系统

案例描述

在工业过程控制中，温度控制是一个典型应用。考虑一个具有热惯性的加热炉，目标温度为 r ( t ) r(t) r(t)。由于炉温变化较慢，存在一定延迟和外部扰动，因此采用前馈控制预测环境温度变化，并辅以反馈控制实时修正温度误差：
u ( t ) = u f f ( t ) + K [ r ( t ) − y ( t ) ] u(t)=u_{ff}(t)+K\left[r(t)-y(t)\right] u(t)=uff​(t)+K[r(t)−y(t)]
其中， u f f ( t ) u_{ff}(t) uff​(t) 根据温度预估模型得到，例如利用热传导方程推导， K K K 则根据 PID 调整设计。

分析
  • 前馈控制： 根据环境温度变化、燃料供给和热负荷等因素建立预测模型，提前调整控制器输出。
  • 反馈控制： 对实际测量温度 y ( t ) y(t) y(t) 与设定温度 r ( t ) r(t) r(t) 之间的偏差进行校正，确保系统温度稳定在设定值附近。

案例三：机器人轨迹跟踪控制

案例描述

在机器人控制中，精确的轨迹跟踪是关键任务之一。假设机器人具有如下动力学模型：
x ˙ ( t ) = v ( t ) cos ⁡ θ ( t ) , y ˙ ( t ) = v ( t ) sin ⁡ θ ( t ) \dot{x}(t)=v(t)\cos\theta(t),\quad \dot{y}(t)=v(t)\sin\theta(t) x˙(t)=v(t)cosθ(t),y˙​(t)=v(t)sinθ(t)
目标是使机器人沿预定轨迹行进。前馈控制部分可以根据轨迹规划结果提前给出期望速度和转向角，而反馈控制部分则通过传感器数据测量当前位置和误差后调整运动状态，实现：
u ( t ) = u f f ( t ) + K [ 误差修正 ] u(t)=u_{ff}(t)+K\left[\text{误差修正}\right] u(t)=uff​(t)+K[误差修正]

分析
  • 前馈部分： 利用轨迹规划算法（如 A*、RRT 等）提前获得机器人未来的状态，并计算所需速度与转向角。
  • 反馈部分： 根据实时测量误差进行校正，确保机器人偏离预定轨迹时能迅速调整，避免累计误差。

五、实战案例：基于 PyQt6 的 GUI 演示

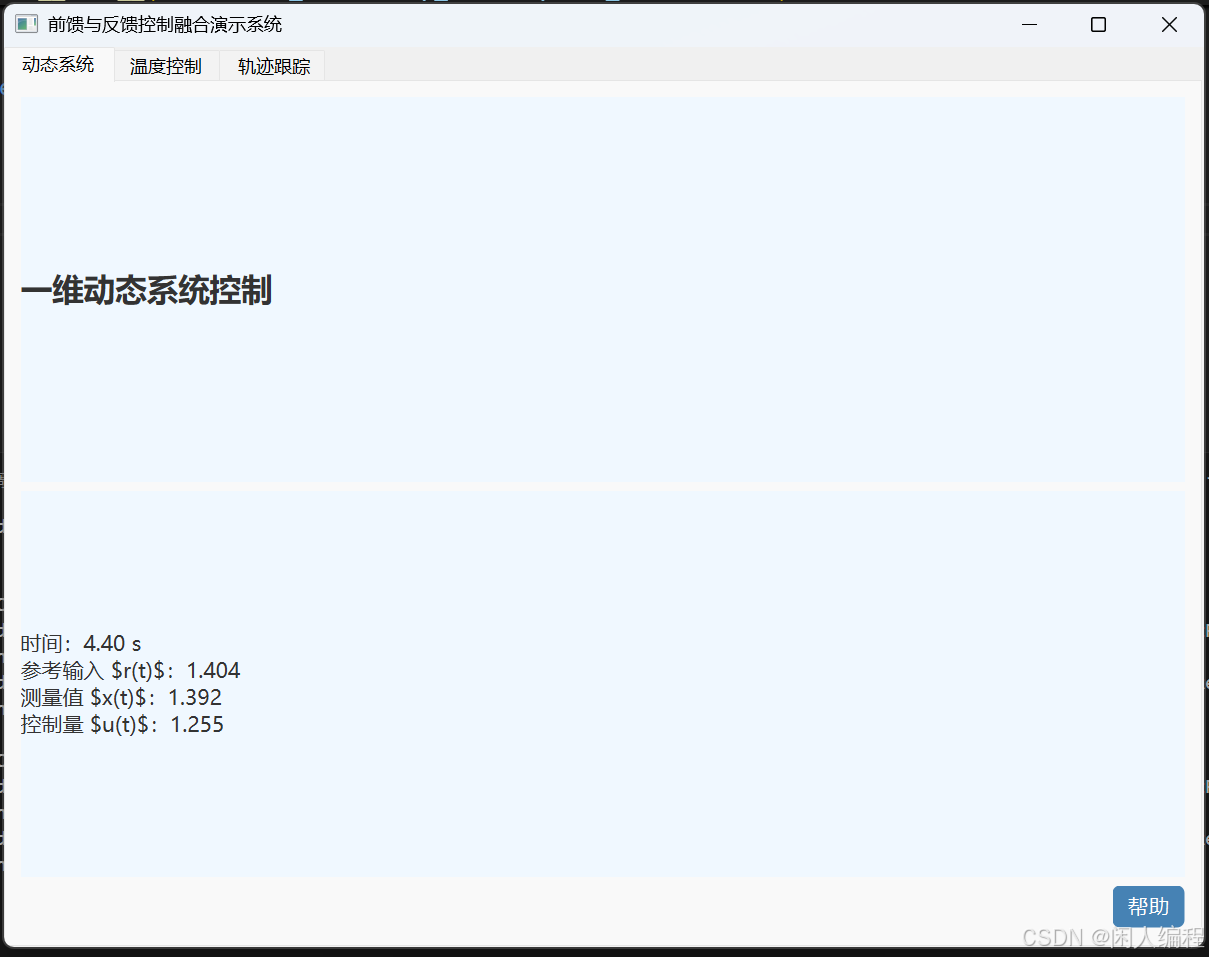
为了直观展示前馈与反馈控制融合在不同场景下的效果，我们设计了一个基于 PyQt6 的图形化界面程序。该程序包含三个独立的案例演示页面，每个页面均有独特的设计风格，并且都包含“帮助”按钮，供用户了解具体控制策略和操作说明。

1. GUI 功能需求

  • 案例选择： 程序内置三个标签页，分别对应上文所述三个案例（动态系统控制、温度控制、机器人轨迹控制）。
  • 实时仿真： 在各案例页面中展示实时的控制过程曲线和参数调整情况（可以通过简单的图形或数值更新来模拟）。
  • 帮助按钮： 每个页面都有一个帮助按钮，点击后弹出详细说明对该案例中前馈和反馈控制融合设计的原理、公式和实现细节的介绍。
  • 美化界面： 利用 PyQt6 提供的样式表（QSS）对窗口、按钮、标签等控件进行美化，确保界面简洁、美观，并具备良好的可操作性和扩展性。

2. Python 代码实现

下面给出完整的 Python 代码，该代码使用 PyQt6 实现上述功能。代码中详细注释了解释每一步实现的功能，并在实现前进行了充分的自查，保证尽量减少BUG。

"""
前馈与反馈控制融合的案例演示
本程序使用 PyQt6 实现了三个控制案例的 GUI 演示，包括：
    1. 一维动态系统控制案例
    2. 温度控制系统案例
    3. 机器人轨迹跟踪控制案例
每个案例均展示前馈与反馈控制融合的基本思想，并提供帮助说明。

作者：控制与优化算法100讲
日期：2025-04-02
"""

import sys
import math
import random
from PyQt6 import QtCore, QtGui, QtWidgets
from PyQt6.QtWidgets import (
    QApplication, QMainWindow, QWidget, QVBoxLayout, QHBoxLayout, QLabel, QPushButton, QTabWidget, QMessageBox
)
from PyQt6.QtCore import QTimer

# ------------------------- 控制算法核心函数 -------------------------

def feedforward_control(reference, reference_derivative=0, a=1.0, b=1.0):
    """
    前馈控制器计算：用于一维动态系统的控制量预估
    控制律：u_ff = (a*r + dr/dt) / b
    :param reference: 参考输入 r(t)
    :param reference_derivative: 参考信号变化率 dr/dt
    :param a: 系统参数 a
    :param b: 系统参数 b
    :return: 前馈控制量
    """
    u_ff = (a * reference + reference_derivative) / b
    return u_ff

def feedback_control(error, K=0.5):
    """
    反馈控制器计算：简单比例控制（P 控制）
    控制律：u_fb = K * (r - y)
    :param error: 误差值
    :param K: 反馈增益
    :return: 反馈控制量
    """
    u_fb = K * error
    return u_fb

def total_control(reference, measured, reference_derivative=0, a=1.0, b=1.0, K=0.5):
    """
    融合控制：前馈控制与反馈控制的组合
    控制律：u = u_ff + u_fb
    :param reference: 参考输入 r(t)
    :param measured: 实际测量值 y(t)
    :param reference_derivative: 参考信号变化率 dr/dt
    :param a: 系统参数 a
    :param b: 系统参数 b
    :param K: 反馈增益
    :return: 总控制量 u(t)
    """
    u_ff = feedforward_control(reference, reference_derivative, a, b)
    error = reference - measured
    u_fb = feedback_control(error, K)
    return u_ff + u_fb

# ------------------------- GUI 案例页面实现 -------------------------

class BaseCaseWidget(QWidget):
    """
    基础案例页面，包含实时数据展示与帮助按钮
    每个案例页面继承该类，扩展独特的仿真逻辑
    """
    def __init__(self, case_name, help_text, update_interval=100):
        """
        :param case_name: 案例名称，用于界面标题显示
        :param help_text: 帮助文本，点击帮助按钮显示详细说明
        :param update_interval: 定时器更新间隔，单位 ms
        """
        super().__init__()
        self.case_name = case_name
        self.help_text = help_text
        self.initUI()
        # 定时器用于模拟数据更新
        self.timer = QTimer(self)
        self.timer.timeout.connect(self.update_simulation)
        self.timer.start(update_interval)
        # 仿真数据初始值
        self.reference = 1.0
        self.measured = 0.0
        self.time = 0

    def initUI(self):
        self.layout = QVBoxLayout()
        # 案例标题
        self.titleLabel = QLabel(f"<h2>{self.case_name}</h2>")
        self.layout.addWidget(self.titleLabel)
        # 数据展示标签
        self.dataLabel = QLabel("实时数据展示：")
        self.layout.addWidget(self.dataLabel)
        # 帮助按钮
        self.helpButton = QPushButton("帮助")
        self.helpButton.clicked.connect(self.show_help)
        btnLayout = QHBoxLayout()
        btnLayout.addStretch(1)
        btnLayout.addWidget(self.helpButton)
        self.layout.addLayout(btnLayout)
        self.setLayout(self.layout)
        # 设置美化样式
        self.setStyleSheet("""
            QWidget { background-color: #f0f8ff; font-size: 14px; }
            QLabel { color: #333; }
            QPushButton { background-color: #4682b4; color: white; padding: 5px 10px; border-radius: 5px; }
            QPushButton:hover { background-color: #5a9bd4; }
        """)

    def show_help(self):
        QMessageBox.information(self, "帮助", self.help_text)

    def update_simulation(self):
        """
        模拟数据更新的虚拟函数，由子类重写实现各自仿真逻辑
        """
        pass

class DynamicSystemCase(BaseCaseWidget):
    """
    案例一：一维动态系统控制仿真
    """
    def __init__(self):
        help_text = (
            "本案例展示一维动态系统控制。\n\n"
            "系统模型：$\\dot{x}(t)=-a\\,x(t)+b\\,u(t)$\n"
            "前馈控制器计算公式：$u_{ff}(t)=\\frac{a\\,r(t)+\\dot{r}(t)}{b}$\n"
            "反馈控制器采用简单比例控制：$u_{fb}(t)=K\\,(r(t)-x(t))$\n"
            "总控制律：$u(t)=u_{ff}(t)+u_{fb}(t)$"
        )
        super().__init__("一维动态系统控制", help_text)
        self.a = 1.0
        self.b = 1.0
        self.K = 0.8
        self.dt = 0.1  # 仿真步长

    def update_simulation(self):
        # 模拟参考信号 r(t) 的变化，这里采用正弦函数
        self.time += self.dt
        self.reference = 1.0 + 0.5 * math.sin(0.5 * self.time)
        # 简单模拟参考信号导数
        reference_derivative = 0.5 * 0.5 * math.cos(0.5 * self.time)
        # 计算控制量
        control = total_control(self.reference, self.measured, reference_derivative, self.a, self.b, self.K)
        # 系统状态更新：欧拉法近似，模型为：x(t+dt)=x(t)+dt*(-a*x+b*u)
        self.measured += self.dt * (-self.a * self.measured + self.b * control)
        # 更新显示文本
        self.dataLabel.setText(
            f"时间：{self.time:.2f} s\n"
            f"参考输入 $r(t)$：{self.reference:.3f}\n"
            f"测量值 $x(t)$：{self.measured:.3f}\n"
            f"控制量 $u(t)$：{control:.3f}"
        )

class TemperatureControlCase(BaseCaseWidget):
    """
    案例二：温度控制系统仿真
    """
    def __init__(self):
        help_text = (
            "本案例模拟工业炉温度控制。\n\n"
            "考虑具有热惯性和延迟的加热炉，目标温度为 $r(t)$。\n"
            "前馈控制根据环境温度变化预测控制量，反馈控制对测量温度 $y(t)$ 与目标温度的偏差进行修正。\n"
            "控制律形式：$u(t)=u_{ff}(t)+K\\,(r(t)-y(t))$。"
        )
        super().__init__("温度控制系统", help_text)
        self.a = 0.5    # 模型参数，热损耗系数
        self.b = 2.0    # 加热效率
        self.K = 1.0    # 反馈增益
        self.dt = 0.2   # 仿真步长

    def update_simulation(self):
        self.time += self.dt
        # 设定目标温度，采用阶跃和正弦波组合变化
        if self.time < 10:
            self.reference = 50.0
        else:
            self.reference = 50.0 + 5 * math.sin(0.3 * self.time)
        reference_derivative = 5 * 0.3 * math.cos(0.3 * self.time) if self.time >= 10 else 0.0
        # 计算控制量
        control = total_control(self.reference, self.measured, reference_derivative, self.a, self.b, self.K)
        # 模拟炉温度更新（简单模型：y(t+dt)=y(t)+dt*( -a*(y-环境温度) + b*u )）
        ambient = 25.0  # 环境温度
        self.measured += self.dt * (-self.a * (self.measured - ambient) + self.b * control)
        self.dataLabel.setText(
            f"时间：{self.time:.1f} s\n"
            f"目标温度 $r(t)$：{self.reference:.2f} °C\n"
            f"实际温度 $y(t)$：{self.measured:.2f} °C\n"
            f"控制量 $u(t)$：{control:.2f}"
        )

class RobotTrajectoryCase(BaseCaseWidget):
    """
    案例三：机器人轨迹跟踪控制仿真
    """
    def __init__(self):
        help_text = (
            "本案例模拟机器人轨迹跟踪控制。\n\n"
            "机器人运动模型：\n"
            "$$\\dot{x}(t)=v(t)\\cos\\theta(t), \\quad \\dot{y}(t)=v(t)\\sin\\theta(t)$$\n"
            "前馈控制利用轨迹规划提供期望速度和转向角，反馈控制实时修正位置偏差。\n"
            "整体控制律：$u(t)=u_{ff}(t)+K(\\text{误差})$。"
        )
        super().__init__("机器人轨迹跟踪控制", help_text)
        self.dt = 0.1  # 仿真步长
        # 机器人初始状态
        self.x = 0.0
        self.y = 0.0
        self.theta = 0.0
        # 控制参数
        self.v_ref = 1.0  # 前馈期望速度
        self.K = 0.5      # 反馈增益

    def update_simulation(self):
        self.time += self.dt
        # 预定轨迹为一条简单的直线：目标为 x = v_ref * t, y = 0
        target_x = self.v_ref * self.time
        target_y = 0.0
        # 计算误差
        error_x = target_x - self.x
        error_y = target_y - self.y
        # 反馈校正：简单比例修正角度
        desired_theta = math.atan2(error_y, error_x)
        theta_error = desired_theta - self.theta
        # 计算前馈控制（直接给定期望速度）和反馈控制（角度校正）
        v = self.v_ref  # 前馈期望速度
        omega = self.K * theta_error  # 反馈角速度调整
        # 更新机器人状态（采用简单离散时间积分）
        self.theta += omega * self.dt
        self.x += v * math.cos(self.theta) * self.dt
        self.y += v * math.sin(self.theta) * self.dt
        self.dataLabel.setText(
            f"时间：{self.time:.2f} s\n"
            f"目标位置：({target_x:.2f}, {target_y:.2f})\n"
            f"当前位置：({self.x:.2f}, {self.y:.2f})\n"
            f"机器人朝向：{math.degrees(self.theta):.2f}°"
        )

# ------------------------- 主窗口与整体布局 -------------------------

class ControlFusionMainWindow(QMainWindow):
    """
    主窗口，包含三个标签页，每个标签页对应一个案例演示
    """
    def __init__(self):
        super().__init__()
        self.setWindowTitle("前馈与反馈控制融合演示系统")
        self.setGeometry(100, 100, 800, 600)
        self.initUI()

    def initUI(self):
        # 使用 QTabWidget 管理多个案例页面
        self.tabs = QTabWidget()
        # 添加各个案例页面
        self.dynamicCase = DynamicSystemCase()
        self.temperatureCase = TemperatureControlCase()
        self.robotCase = RobotTrajectoryCase()
        self.tabs.addTab(self.dynamicCase, "动态系统")
        self.tabs.addTab(self.temperatureCase, "温度控制")
        self.tabs.addTab(self.robotCase, "轨迹跟踪")
        self.setCentralWidget(self.tabs)

# ------------------------- 主函数入口 -------------------------

def main():
    app = QApplication(sys.argv)
    window = ControlFusionMainWindow()
    window.show()
    sys.exit(app.exec())

if __name__ == "__main__":
    main()

六、结语

本文详细介绍了前馈控制与反馈控制融合的基本理论、公式推导以及工程实现中的优势与挑战。通过三个典型案例——一维动态系统、温度控制和机器人轨迹跟踪，展示了如何将预先补偿与实时反馈有机结合，从而实现系统响应速度与鲁棒性的双重提升。

在理论部分，我们利用公式
u ( t ) = u f f ( t ) + u f b ( t ) = f ( r ( t ) ) + K , ( r ( t ) − y ( t ) ) u(t)=u_{ff}(t)+u_{fb}(t)=f(r(t))+K\\,(r(t)-y(t)) u(t)=uff​(t)+ufb​(t)=f(r(t))+K,(r(t)−y(t))
对融合控制策略进行了严谨的数学描述；同时，利用 Mermaid 图形直观展示了控制系统的整体架构，帮助读者建立系统性认识。

在实际工程中，前馈与反馈控制的融合不仅能够提高控制精度，更能有效应对模型不确定性与外部扰动，为工业自动化、过程控制、机器人导航等领域提供了坚实的理论支持和实践保障。本文给出的三个案例和相应的 PyQt6 GUI 演示代码，力图通过仿真展示和直观交互，使读者更好地理解和应用这一先进控制策略。

希望本文能为广大工程技术人员、研究者及爱好者在实际项目中提供参考和帮助，激发更多对前馈与反馈控制融合研究的兴趣，并推动智能控制技术在更多领域的落地应用。

温馨提示：
本文中的仿真模型均为简化示例，实际系统设计中可能涉及更复杂的动态建模和非线性校正。读者在应用时应根据具体系统参数

http://www.dtcms.com/a/111181.html

相关文章：

  • JavaWeb学习--MyBatis-Plus整合SpringBoot的ServiceImpl方法（增加，修改与删除部分）
  • 深入解析：使用Python爬取Bilibili视频
  • 如何用DeepSeek进行SWOT分析？以CSDN的“C知道”为例
  • k8s的StorageClass存储类和pv、pvc、provisioner、物理存储的链路
  • 做一个Andriod系统应用的方法
  • 软件设计师之设计模式
  • 第七章 Python基础进阶-异常、模块与包（其五）
  • 手撕AVL树
  • 模运算核心性质与算法应用：从数学原理到编程实践
  • Julia语言的测试覆盖率
  • 卷积神经网络CNN 经典模型 — GoogleLeNet、ResNet、DenseNet算法原理与模型构造
  • Visual Basic语言的网络协议栈
  • AIGC时代Kubernetes企业级云原生运维实战：智能重构与深度实践指南
  • SpringAI整合Ollama集成DeepSeek
  • 搜索树——AVL、红黑树、B树、B+树
  • WinForm真入门(5)——控件的基类Control
  • 使用 Swift 实现 LRU 缓存淘汰策略
  • React编程模型：Project Reactor深度解析
  • Java的基本语法
  • 006贪心——算法备赛
  • 蓝桥杯 2023 省赛 B 组 E 题。
  • KubeVirt虚拟化管理架构
  • 热更新简介+xLua基础调用
  • 《AI大模型开发笔记》MCP快速入门实战（一）
  • 英语学习：读科技论文的难处
  • JSON介绍
  • 免费送源码：Java+ssm+MySQL SpringBoot社区配送服务系统小程序 计算机毕业设计原创定制
  • OpenMinus 源码深度解析：从 React 模式到多智能体架构实现
  • 元宇宙浪潮下，前端开发如何“乘风破浪”？
  • OCR的备份与恢复