约瑟夫环的四种(数组,链表,递归,迭代)解决方案,与空间、时间复杂度分析
以下方法均没有考虑结果集的空间与时间复杂度
1.数组解法
实现代码(未优化)
class Main {
public static void main(String[] args){
Scanner read = new Scanner(System.in);
int n = read.nextInt();
int m = read.nextInt();
int[] people = new int[n]; // 初始化数组(0表示存活,1表示出局)
int currentIndex = 0; // 当前指针
int count = 0; // 计数器
int alive = n; // 存活人数
List<Integer> sequence = new ArrayList<>();// 用来输出出局顺序的,与算法无关
while (alive > 0) {
if (people[currentIndex] == 0) {
count++;
if (count == m) {
people[currentIndex] = 1; // 标记出局
sequence.add(currentIndex + 1); // 记录编号(这里加一是因为编号是从1开始,而数组是从0开始)
count = 0; // 重新计数
alive--;
}
}
currentIndex = (currentIndex + 1) % n; // 模拟环形移动
}
// 输出结果
for (int i = 0; i < n; i++) {
if (i != 0) {
System.out.print(" ");
}
System.out.print(sequence.get(i));
}
}
}这个算法就是使用程序来模拟现实实际运行的情况
思路
-
使用数组标记人员状态(存活/出局)。
-
通过循环遍历数组计数存活者,找到第 m 个存活者后标记为出局。
时间复杂度
-
单次出局操作:需要遍历 m ~(m+n)个存活者(因为会遍历到已经出局的人)。
-
总时间复杂度:需处理 n 次出局,每次遍历 m ~(m+n)次,总时间复杂度约为 O(n*m) ~ O(n*m+n²)。也就是 O(n²),当m很大的时候(并没有规定m一定要小于n!!!),这个算法是很亏的。
空间复杂度
-
数组需 O(n) 空间,总空间复杂度为 O(n)。
优化点
如果考虑到m很大的情况,这段代码就又可以优化了。
当m大于现存活人生时,会出现重复遍历的情况,下面举一个例子:
假设 n=5,m=7,存活人数初始为 5:
-
第一轮有效步数
7%5=2,第二个人出局(编号 2)。 -
存活人数变为 4,有效步数
7%4=3,第三个人出局(编号 5)。 -
存活人数变为 3,有效步数
7%3=1,第一个人出局(编号 1)。 -
存活人数变为 2,有效步数
7%2=1,下一个人出局(编号 3)。 -
最后剩下编号 4 的人,出局顺序为
2 5 1 3 4。
通过取余优化,避免了每次遍历完整的 m 次,显著提升了效率。
优化后数组解法
import java.util.*;
class Main {
public static void main(String[] args) {
Scanner read = new Scanner(System.in);
int n = read.nextInt();
int m = read.nextInt();
int[] people = new int[n];
int currentIndex = 0;
int count = 0;
int alive = n;
List<Integer> sequence = new ArrayList<>();
while (alive > 0) {
// 计算有效步数(取余优化)
int effectiveM = m % alive;
if (effectiveM == 0) {
effectiveM = alive;
}
if (people[currentIndex] == 0) {
count++;
if (count == effectiveM) { // 用有效步数代替原m
people[currentIndex] = 1;
sequence.add(currentIndex + 1);
count = 0;
alive--;
}
}
currentIndex = (currentIndex + 1) % n;
}
// 输出结果
for (int i = 0; i < n; i++) {
if (i != 0) {
System.out.print(" ");
}
System.out.print(sequence.get(i));
}
}
}优化后的时间复杂度与空间复杂度
-
单次出局操作:经过取余操作后,有效步数的范围在 1 ~ n 之间。
-
总时间复杂度:仍需处理 n 次出局,每次遍历 1 ~ n 次,总时间复杂度在 O(n) ~ O(n²) 之间,平均来说仍属于平方阶
-
空间复杂度 :总空间复杂度为 O(n)
2.链表解法
实现代码
import java.util.*;
class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
LinkedList<Integer> list = new LinkedList<>();
for (int i = 1; i <= n; i++) list.add(i);
ArrayList<Integer> sequence = new ArrayList<>();
int currentIndex = 0;
while (!list.isEmpty()) {
currentIndex = (currentIndex + m - 1) % list.size();
sequence.add(list.remove(currentIndex));
}
// 输出结果
for (int i = 0; i < n; i++) {
if (i != 0) System.out.print(" ");
System.out.print(sequence.get(i));
}
}
}思路
-
实际上和数组解法类似,都是使用程序直接模拟实际行为。
-
和数组不同的是,数组是使用标记来判断是否存活,而链表会将出局人移出,可以减少运行到后面的遍历数量。
时间复杂度
-
单次删除操作:
LinkedList的remove(int index)方法平均需要 O(n) 时间,但是n会随着链表的缩短而减小,最终减少到1,所以单次的删除操作的时间复杂度在 O(1) ~ O(n) 。 -
总时间复杂度:和优化后的数组类似,进行 n 次删除操作,总时间复杂度为 O(n) ~ O(n²),仍属于平方阶
空间复杂度
-
链表和结果列表各需 O(n) 空间,总空间复杂度为 O(n)。
3.递归解法
参考笔记
实现代码
import java.util.*;
class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
List<Integer> sequence = new ArrayList<>();
for (int i = 1; i <= n; i++) {
sequence.add(dg(n, m, i) + 1); // 加一是因为编号从 1 开始
}
// 输出出局顺序
for (int i = 0; i < n; i++) {
if (i != 0) {
System.out.print(" ");
}
System.out.print(sequence.get(i));
}
}
// 递归函数,计算第 i 轮出局的人的编号
public static int dg(int n, int m, int i) {
if (i == 1) {
// 当只剩一个人时,直接返回最后一个人的编号(从 0 开始,所以要减1)
return Math.floorMod(m - 1,n) ;//可以看作(m-1+n)% n
}
// 递归计算上一轮的结果,并加上 M 后取模
return (dg(n - 1, m, i - 1) + m) % n;
}
}思路
-
这段代码的解法思路就是将每一次淘汰人员都看作第一次淘汰,即下标都是从0开始
-
递归就是为了计算淘汰出的人员的 原始下标 是多少
新一轮中的编号:(旧一轮中的编号 - M)% 剩余人数
eg:m=3
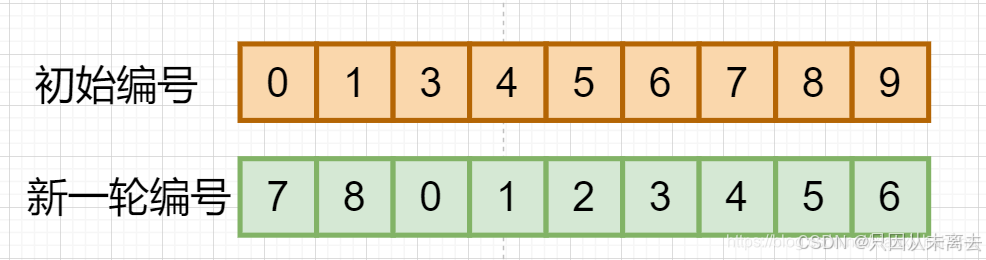
因为每一次都从0开始数m个,所以将每一次的新一轮编号都减去m使其每次都是从0开始计数
这时有人就要问了,我们在原本和谐的顺序中删除了一个2,不会使后续不连贯(少了个2,多了个9)吗?
这就是这个 (旧一轮中的编号 - M)% 剩余人数 的妙处,他不仅能将需要约束在 0~(n-1)之间(因为淘汰了1人,9这个需要应该要剔除,最大值应该为8),还能将之前删掉的数据归入到n-1与0之间也就是8和0之间,这时候我们又能重新将其看成第一次在 n = 9,m=3 中淘汰玩家
这就印证了递归解法的核心思路:
-
每一次淘汰人员都看作第一次淘汰
那么,旧一轮中的编号:(新一轮的编号 + M)% 剩余人数
通过这个公式我们就能在每一层递归中保留上一层原始的下标
-
时间复杂度
-
单次出局操作:每一次需要递归i层,i的值从1到n递增,所以单次时间复杂度在为 O(1)到O(n) 并为累加式
-
总时间复杂度:需处理 n 次出局,每次遍历 1 ~ n 次,由等差数列求和公式可得总时间复杂度为
也就是平方阶 O(n²) 而且会比较稳定。
如果是只计算最终幸存人员的方式就为O(n),因为他不需要像链表与数组一样依赖其他人的淘汰状态
空间复杂度
递归解法的主要空间开销来自于递归调用栈的深度。在每次递归调用 dg(n, m, i) 时,递归的深度为 i 层(例如,当计算第 i 轮出局时,需要递归 i 次)。由于主函数中对每个 i(从 1 到 n)都调用了一次递归函数,因此最大递归深度出现在计算最后一轮(i = n)时,此时递归深度为 n 层。
因此,空间复杂度为 O(n),由递归调用栈的最大深度决定。
4.迭代解法
实现代码
import java.util.*;
class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
List<Integer> sequence = new ArrayList<>();
for (int i = 1; i <= n; i++) {
int current_k = n - i + 1; // 当前剩余人数
int pos = (m - 1) % current_k; // 初始位置
// 逐步计算在原始环中的位置
for (int j = current_k + 1; j <= n; j++) {
pos = (pos + m) % j;
}
sequence.add(pos + 1);
}
// 输出出局顺序
for (int i = 0; i < n; i++) {
if (i != 0) System.out.print(" ");
System.out.print(sequence.get(i));
}
}
}思路
-
迭代解法和递归解法的思路是一致的,这种简单且深度固定的递归大多都能转化为某一公式的循环调用
-
迭代解法其实是递归解法的优化版本,递归解法存在递归调用栈的开销,可能会导致栈溢出问题。而迭代解法通过循环的方式避免了递归调用栈的使用,直接从最底层的情况开始逐步向上计算,最终得到所需的结果。
-
迭代解法同样基于递归解法中的核心递推公式: 旧一轮中的编号 = (新一轮的编号 + M) % 剩余人数
时间复杂度
-
计算方式和递归方式一致
-
单次出局操作:每一次计算需要循环
i次,i的值从 1 到n递增。 -
总时间复杂度:需处理
n次出局,每次遍历1 ~ n次,由等差数列求和公式可得总时间复杂度为也就是平方阶 O(n²) ,
-
同理如果是只计算最终幸存人员的方式就为O(n)
空间复杂度
- 通过数学公式直接计算,避免了递归调用栈的开销,空间复杂度为 O(1) 在实际应用中比递归解法更加稳定,尤其是在处理大规模数据时。
