当前位置：首页 > news >正文

LeetCode-547. 省份数量

news 2025/7/19 13:34:48

1、题目描述：

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中省份的数量。

示例 1：

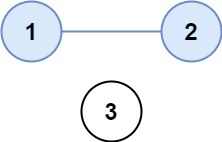
输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例 2：

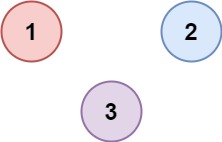
输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

提示：

1 <= n <= 200
n == isConnected.length
n == isConnected[i].length
isConnected[i][j] 为 1 或 0
isConnected[i][i] == 1
isConnected[i][j] == isConnected[j][i]

2、代码：

#include <vector>
#include <functional>  // 用于lambda表达式

using namespace std;

class Solution {
public:
    int findCircleNum(vector<vector<int>>& isConnected) {
        // 获取城市数量
        int n = isConnected.size();
        if (n == 0) return 0;

        // 初始化并查集数据结构
        vector<int> parent(n);   // parent[i]表示i的父节点
        vector<int> rank(n, 1); // rank[i]表示以i为根的树的高度（用于按秩合并）

        // 初始时每个城市自成一类，父节点指向自己
        for (int i = 0; i < n; ++i) {
            parent[i] = i;
        }

        // 查找函数（带路径压缩）
        // 作用：找到x的根节点，并将路径上的节点直接指向根（降低后续查找复杂度）
        function<int(int)> find = [&](int x) {
            if (parent[x] != x) {
                parent[x] = find(parent[x]);  // 递归压缩路径
            }
            return parent[x];
        };

        // 合并函数（按秩合并优化）
        // 作用：将x和y所在的集合合并为一个集合
        auto unite = [&](int x, int y) {
            int rootX = find(x);  // 找到x的根
            int rootY = find(y);  // 找到y的根
            
            // 关键修复：必须检查根是否相同，否则会导致错误合并
            if (rootX == rootY) return;  // 已在同一集合中，无需合并

            // 按秩合并：将小树合并到大树下以保持平衡
            if (rank[rootX] < rank[rootY]) {
                parent[rootX] = rootY;  // 将rootX的父设为rootY
            } else {
                parent[rootY] = rootX;  // 将rootY的父设为rootX
                // 若两树高度相同，合并后树的高度+1
                if (rank[rootX] == rank[rootY]) {
                    ++rank[rootX];  // 仅在两树同高时增加秩
                }
            }
        };

        // 遍历邻接矩阵的上三角部分（利用对称性避免重复处理）
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {  // 仅处理i<j的情况
                if (isConnected[i][j] == 1) {  // 发现相连城市
                    unite(i, j);  // 合并集合
                }
            }
        }

        // 统计连通分量数量（即根节点数量）
        int provinces = 0;
        for (int i = 0; i < n; ++i) {
            // 根节点的特征是：find(i) == i
            if (find(i) == i) {
                ++provinces;
            }
        }

        return provinces;
    }
};