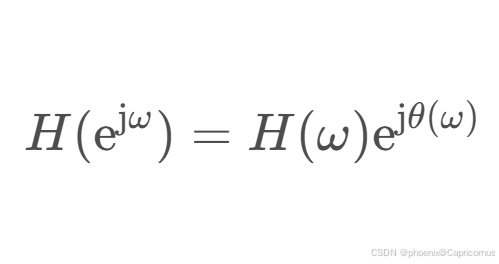H(e^j\omega) H(\omega)

$H({\mathrm{e}}^{\mathrm{j}\omega })$和$H(\omega )$的区别

曾经和廖老师讨论过这个问题，频域函数就是$\omega$的函数，为什么写成$H({\mathrm{e}}^{\mathrm{j}\omega })$的形式，当时我们讨论的结果是为了和$\mathcal{Z}$变换建立联系，$z={\mathrm{e}}^{\mathrm{j}\omega }$。其实是为了与幅度函数$H(\omega )$的区分。由于图像处理中的滤波器设计普遍是零相位滤波器，所以罕见$H({\mathrm{e}}^{\mathrm{j}\omega })$的形式。

FIR数字滤波器的单位脉冲响应$h(n)$是有限长的，其频率响应可写成幅频响应和相频响应相乘的形式，

$$H({\mathrm{e}}^{\mathrm{j}\omega })=|H({\mathrm{e}}^{\mathrm{j}\omega })|{\mathrm{e}}^{\mathrm{j}\arg [H({\mathrm{e}}^{\mathrm{j}\omega })]}$$

其中，$|H({\mathrm{e}}^{\mathrm{j}\omega })|$称作滤波器的幅频响应，$\arg [H({\mathrm{e}}^{\mathrm{j}\omega })]$称作滤波器的相频响应。

在讨论线性相位 FIR 数字滤波器的设计时，一般把频率响应写成幅度函数和相位函数相乘的形式

$$H({\mathrm{e}}^{\mathrm{j}\omega })=H(\omega ){\mathrm{e}}^{\mathrm{j}\theta (\omega )}$$

其中，$H(\omega )$称作滤波器的幅度函数，$\theta (\omega )$称作滤波器的相位函数。

可以看出，幅度函数不等于幅频响应，幅度函数$H(\omega )$可正可负，相位函数也不等于相频响应，二者之间存在 0 或$\pi$的相位差。