K-means算法
目录
1. 前言
2. K-means
3. 理论基础
4. 优缺点分析
5. 实验
1. 前言
通俗版 K-means 解释
想象一下,你是一个教练,现在有一群人需要分成 K 个队伍。你的任务就是合理分组,让每个队伍内部的人尽可能相似(比如身高相近、兴趣相似等)。
具体步骤是这样的:
-
随机选队长:你随便指定 K 个人作为初始的“队长”(也就是 聚类中心)。
-
第一次站队:每个人观察自己和哪个队长最接近(比如距离最近),然后站到对应的队伍里。
-
队长重新调整位置:每个队伍的队长不能一直原地不动,于是你让他们移动到当前队伍成员的平均位置(也就是新的中心点)。
-
重新站队:大家再次看看自己离哪个新队长最近,调整队伍。
-
重复调整:不断重复 “站队 → 队长调整位置” 这个过程,直到队伍不再有明显变化(也就是聚类趋于稳定)。
最终结果:这时候,每个人都站在了自己最合适的队伍里,而队长也处在了最佳位置,这就是 K-means 完成聚类 的状态!
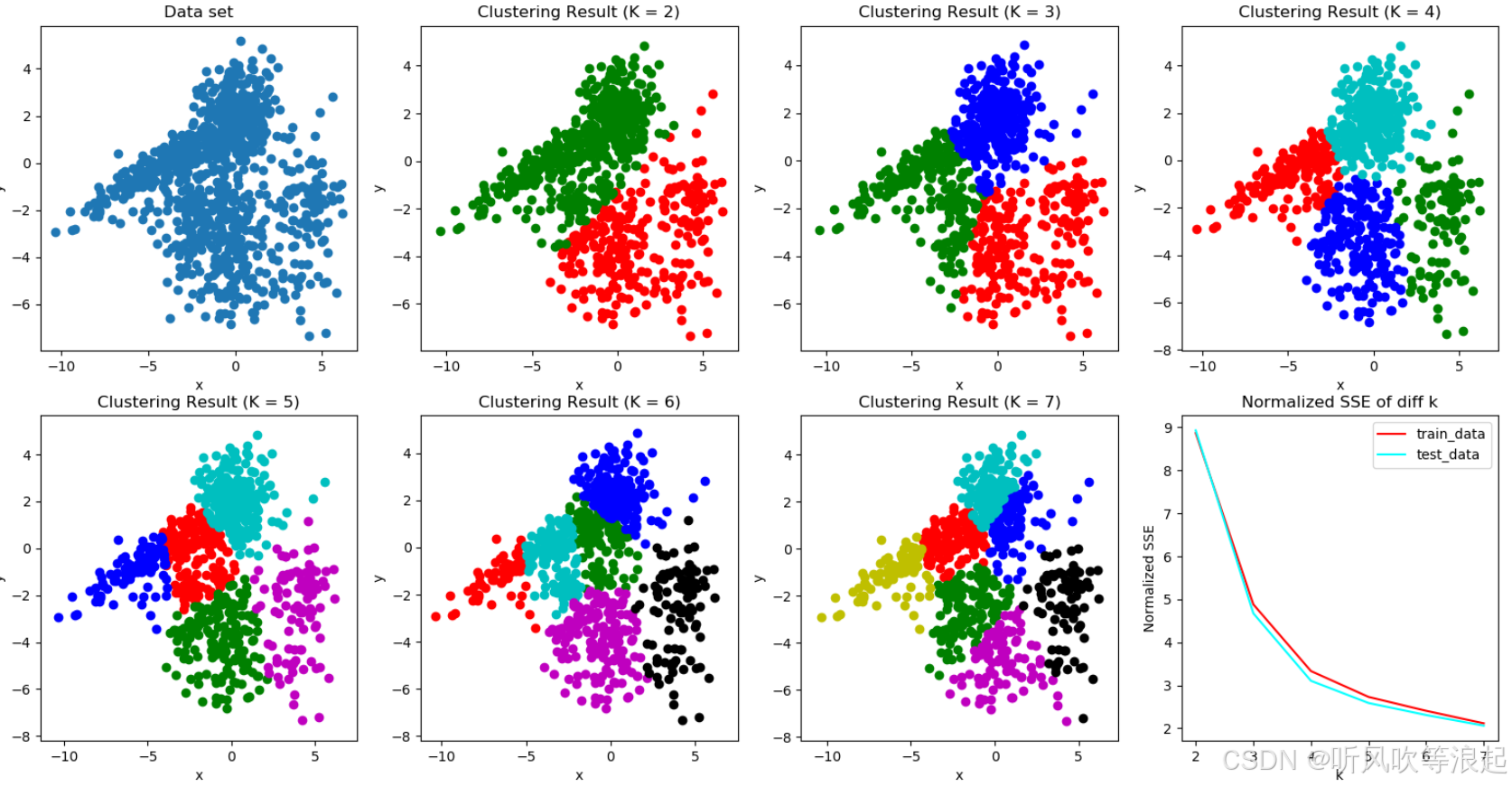
补充说明
-
K 值怎么选? 这个需要提前设定,比如你想分成 3 类,K 就是 3。
-
“最近”怎么算? 通常用欧氏距离(直线距离),但也可以根据需求换其他距离度量方式。
-
什么时候停止? 当队长位置几乎不再移动,或者队伍成员不再变化时,算法就可以停止了。
这个优化版本在保持原意的基础上:
-
结构更清晰(分步骤+补充说明)
-
语言更生动(比喻+互动感)
-
补充关键细节(如 K 值选择、距离计算、停止条件)
-
增加可读性(表情符号+重点标注)
2. K-means
K-means 是机器学习中最经典、应用最广泛的无监督聚类算法之一,它的核心目标是将一组数据自动划分为 K 个簇(cluster),使得:
-
同一簇内的数据点尽可能相似(距离近)
-
不同簇之间的数据点尽可能不同(距离远)
该算法通过迭代优化的方式,不断调整簇的中心(称为质心),最终使得所有数据点到其所属质心的距离之和最小(即最小化簇内误差平方和)。
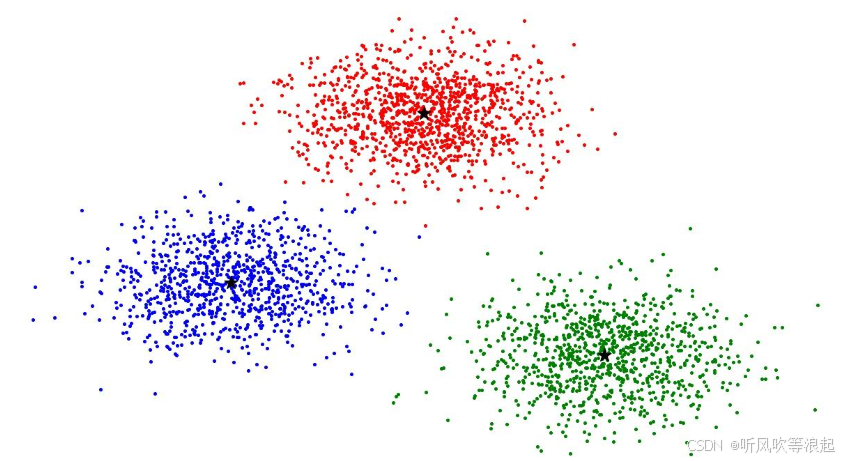
K-means 算法步骤详解
1. 初始化质心(Initialization)
-
随机选取 K 个数据点作为初始质心(即“代表”)。
-
K 的值需要预先设定(可通过肘部法则、轮廓系数等方法选择最优 K)。
2. 分配数据点(Assignment Step)
-
计算每个数据点到所有质心的距离(通常使用欧氏距离)。
-
将数据点分配到离它最近的质心所在的簇,形成 K 个初始分组。
3. 更新质心(Update Step)
-
重新计算每个簇的质心(取簇内所有数据点的均值作为新质心)。
-
质心的位置会随着数据点的分配而不断调整。
4. 迭代优化(Iteration)
-
重复步骤 2 和 3,直到满足停止条件:
-
质心位置不再变化(收敛);
-
数据点的簇分配不再改变;
-
达到最大迭代次数(防止无限循环)。
-
算法特点与注意事项
✅ 优点
-
简单高效,适用于大规模数据集。
-
易于实现,计算复杂度较低(线性复杂度 O(n))。
⚠️ 局限性
-
需要预先指定 K 值,选择不当可能影响聚类效果。
-
对初始质心敏感,不同初始值可能导致不同结果(可用 K-means++ 优化初始化)。
-
仅适用于凸形簇,对非球形簇或复杂分布效果不佳(可尝试 DBSCAN、谱聚类 等替代方法)。
-
受异常值影响较大(可使用 K-medoids 等鲁棒性更强的变体)。
总结
K-means 通过交替执行“分配-更新”步骤,使质心逐步移动到最佳位置,最终实现数据的高效聚类。虽然它有一些限制,但因其简单、快速、可解释性强,仍然是数据挖掘、图像分割、客户分群等领域的首选算法之一。
3. 理论基础
1. 目标函数的数学表述
K-means 算法的核心目标是最小化簇内平方误差和(Within-Cluster Sum of Squares, WCSS),其数学表达式为:
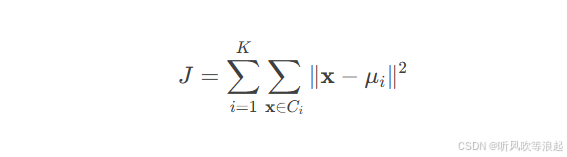
其中:
-
K:预先设定的簇数量
-
Ci:第 i 个簇的数据点集合
-
μi:第 i 个簇的质心(均值向量)
-
x:数据点
-
∥x−μi∥:数据点 x 与质心 μi 的欧几里得距离
目标解释:
最小化 J 意味着让同一簇内的数据点尽可能靠近质心,从而保证簇内相似性最大化。
2. 算法完整流程
K-means 通过迭代优化逐步逼近目标函数的最小值,具体步骤如下:
Step 1: 初始化质心
-
随机选择 K 个数据点作为初始质心 {μ1,μ2,...,μK}。
-
改进建议:使用 K-means++ 初始化,避免质心过于接近,提升收敛速度。
Step 2: 分配数据点到最近质心(簇分配)
-
对每个数据点 x,计算其与所有质心的欧氏距离:
d(x,μi)=∥x−μi∥
-
将 x 分配到距离最近的质心所属的簇 Ci:
Ci={x∣argmini∥x−μi∥2}
Step 3: 重新计算质心(均值更新)
-
对每个簇 Ci,重新计算质心 μiμi 为该簇所有数据点的均值:
μi=1∣Ci∣∑x∈Cix
-
注:若簇为空(无数据点),可删除该簇或重新初始化质心。
Step 4: 迭代直至收敛
-
重复 Step 2 和 Step 3,直到满足以下任一停止条件:
-
质心位置不再变化(μinew=μiold)。
-
目标函数 J 的变化量小于预设阈值(如 ΔJ<ϵ)。
-
达到最大迭代次数(防止无限循环)。
-
3. 关键问题与优化
-
初始质心敏感性
-
问题:随机初始化可能导致局部最优解。
-
解决方案:使用 K-means++,优先选择相距较远的点作为初始质心。
-
-
距离度量选择
-
默认使用欧氏距离(适用于连续型数据)。
-
其他场景:余弦相似度(文本聚类)、曼哈顿距离(离散数据)。
-
-
K值确定方法
-
肘部法则(Elbow Method):观察不同 K 值对应的 J 值,选择拐点。
-
轮廓系数(Silhouette Score):衡量簇内紧密度和簇间分离度。
-
-
异常值处理
-
问题:均值易受极端值影响。
-
改进:使用 K-medoids(以中位数代替均值)或提前剔除异常值。
-
4. 算法总结
K-means 通过交替执行**“分配-更新”步骤,将目标函数 J 逐步优化至收敛。其优势在于简单高效,但需注意以下局限性:
-
仅适用于凸形簇(球形分布)。
-
需预先指定 K值。
-
对初始质心和异常值敏感。
适用场景:客户分群、图像压缩、文档聚类等低维数据任务。
改进方向:结合 PCA 降维、尝试谱聚类或 DBSCAN 处理复杂分布。
4. 优缺点分析
K-means 因其简单高效的特点,被广泛应用于以下领域:
-
聚类分析(Clustering Analysis)
-
核心用途:发现数据内在的分组模式,将相似样本归为同一簇。
-
典型场景:
-
客户细分(如电商用户行为分析)
-
文档主题分类(新闻、论文聚类)
-
基因表达数据分组(生物信息学)
-
-
-
图像处理(Image Segmentation)
-
核心用途:将像素按颜色或空间位置聚类,实现图像分割。
-
案例:
-
医学图像中的肿瘤区域识别
-
自动驾驶中的道路与障碍物划分
-
-
-
数据压缩(Data Compression)
-
核心用途:用簇质心代表原始数据,减少存储量(如颜色量化)。
-
案例:
-
将 24 位真彩色图像压缩为 256 色(K=256)
-
时间序列数据的简化表示
-
-
-
异常检测(Anomaly Detection)
-
核心用途:远离所有质心的数据点可视为异常值。
-
二、K-means 的优缺点深度解析
✅ 优点
-
简单易用
-
算法逻辑直观,适合作为聚类任务的入门方法。
-
-
计算高效
-
时间复杂度为 O(n·K·T)(n 为样本数,T 为迭代次数),适合大规模数据。
-
-
可扩展性强
-
可通过批处理(Mini-Batch K-means)进一步加速。
-
⚠️ 缺点与局限性
-
需预先指定 K 值
-
解决方法:结合肘部法则或轮廓系数选择最优 K。
-
-
对初始质心敏感
-
改进方案:使用 K-means++ 初始化质心。
-
-
仅适用于凸形簇
-
局限性:无法处理环形、流形等复杂结构(需改用 DBSCAN 或谱聚类)。
-
-
对噪声和异常值敏感
-
改进方案:数据预处理(去噪)或使用 K-medoids(基于中位数)。
-
-
依赖欧氏距离
-
问题:高维数据中欧氏距离可能失效(需降维或改用余弦相似度)。
-
三、使用 K-means 的前提条件
-
已知簇数量(K)
-
若 K 未知,需通过实验或指标(如 Gap Statistic)确定。
-
-
数据尺度一致
-
必须对特征进行标准化(如 Z-score),避免量纲影响距离计算。
-
-
数据分布假设
-
理想情况下,各簇应为球形分布且大小相近。
-
-
样本独立性
-
数据点之间应相互独立,无强相关性。
-
四、何时选择/避免使用 K-means?
✔️ 适用情况
-
数据量较大,需快速聚类。
-
簇形状接近球形,且边界清晰。
-
特征维度较低(可通过 PCA 降维后处理高维数据)。
❌ 不适用情况
-
簇形状复杂(如嵌套环形、螺旋形)。
-
数据含大量噪声或异常值。
-
不同簇的密度或大小差异显著。
五、改进方案与替代算法
| 问题 | 解决方案 |
|---|---|
| K 值不确定 | 肘部法则、轮廓系数、Gap Statistic |
| 初始质心敏感 | K-means++ 初始化 |
| 异常值影响 | 改用 K-medoids 或 RobustScaler 预处理 |
| 非凸形簇 | DBSCAN、谱聚类、GMM |
| 高维数据距离失效 | PCA 降维或改用 t-SNE + K-means |
六、总结
K-means 是聚类任务的基准算法,适合处理低维、球形分布、规模适中的数据。在实际应用中,需结合数据特性选择预处理方法或替代算法,并注意以下关键点:
-
标准化数据(避免尺度差异)
-
合理选择 K 值(结合评估指标)
-
尝试多次初始化(减少局部最优影响)
如果需要处理更复杂的数据分布,可探索 层次聚类、DBSCAN 或高斯混合模型(GMM) 等进阶方法。
5. 实验
代码:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
# 1. 生成500个随机平面点 (范围: 0-100)
np.random.seed(42) # 设置随机种子保证结果可复现
points = np.random.rand(500, 2) * 100
# 2. 使用K-means分类 (假设分为4类)
k = 4 # 聚类数量
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(points)
labels = kmeans.labels_
centers = kmeans.cluster_centers_
# 3. 可视化结果
plt.figure(figsize=(10, 8))
# 绘制所有点,按分类着色
colors = ['red', 'blue', 'green', 'purple', 'orange', 'cyan', 'magenta', 'yellow']
for i in range(k):
cluster_points = points[labels == i]
plt.scatter(cluster_points[:, 0], cluster_points[:, 1],
c=colors[i], label=f'Cluster {i+1}', alpha=0.6)
# 绘制聚类中心
plt.scatter(centers[:, 0], centers[:, 1], c='black', marker='X', s=200, label='Centroids')
plt.title(f'K-means Clustering of 500 Random Points (k={k})')
plt.xlabel('X coordinate')
plt.ylabel('Y coordinate')
plt.legend()
plt.grid(True)
plt.show()
# 4. 打印聚类中心坐标
print("Cluster Centers:")
for i, center in enumerate(centers):
print(f"Cluster {i+1}: ({center[0]:.2f}, {center[1]:.2f})")输出:
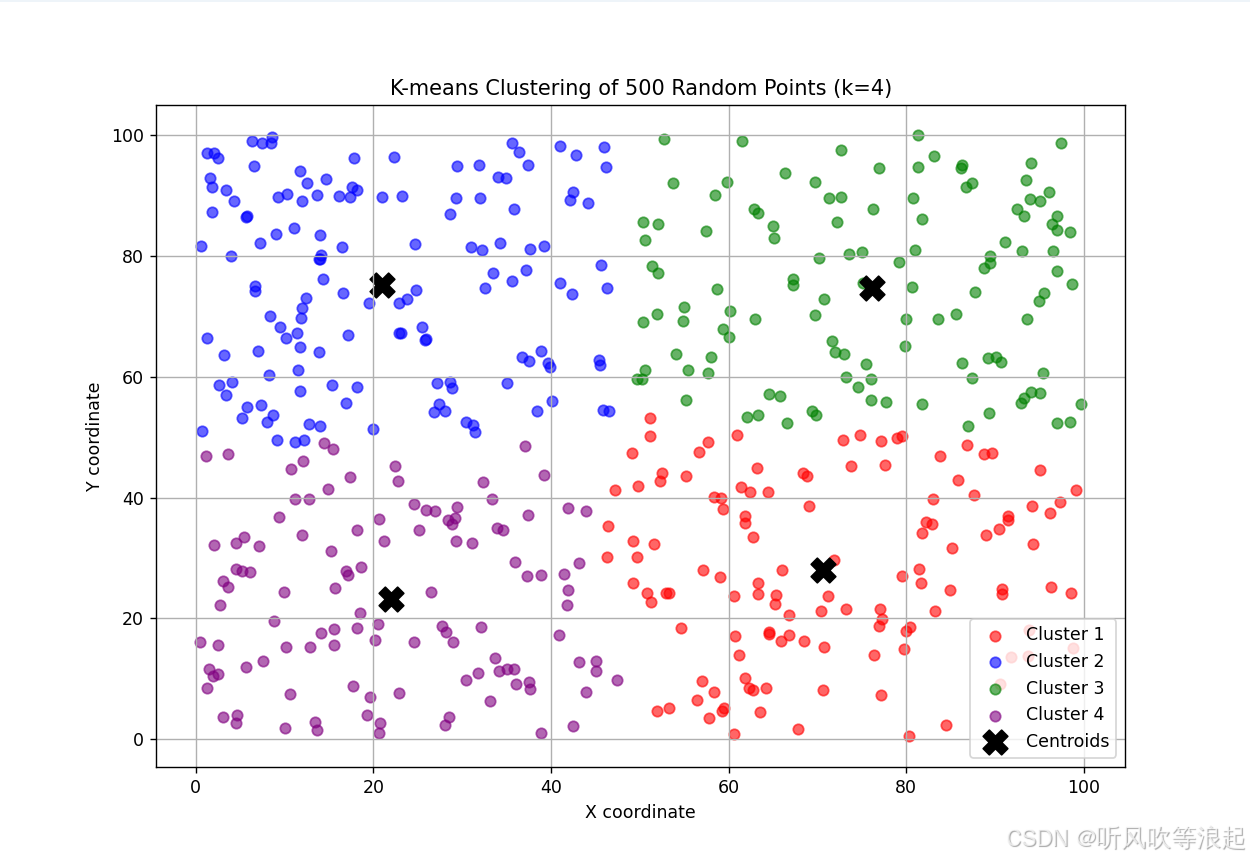
控制台显示:
Cluster Centers:
Cluster 1: (70.64, 28.03)
Cluster 2: (20.98, 75.23)
Cluster 3: (76.08, 74.62)
Cluster 4: (21.96, 23.20)
