二分查找算法精讲

资料来源 二分查找红蓝染色法https://www.bilibili.com/video/BV1AP41137w7?vd_source=02eff3861fbae92e5089ad13f3b33f20&spm_id_from=333.788.videopod.sections

二分查找原理&闭区间写法

34. 在排序数组中查找元素的第一个和最后一个位置

34. 在排序数组中查找元素的第一个和最后一个位置

关键的对与区间的定义

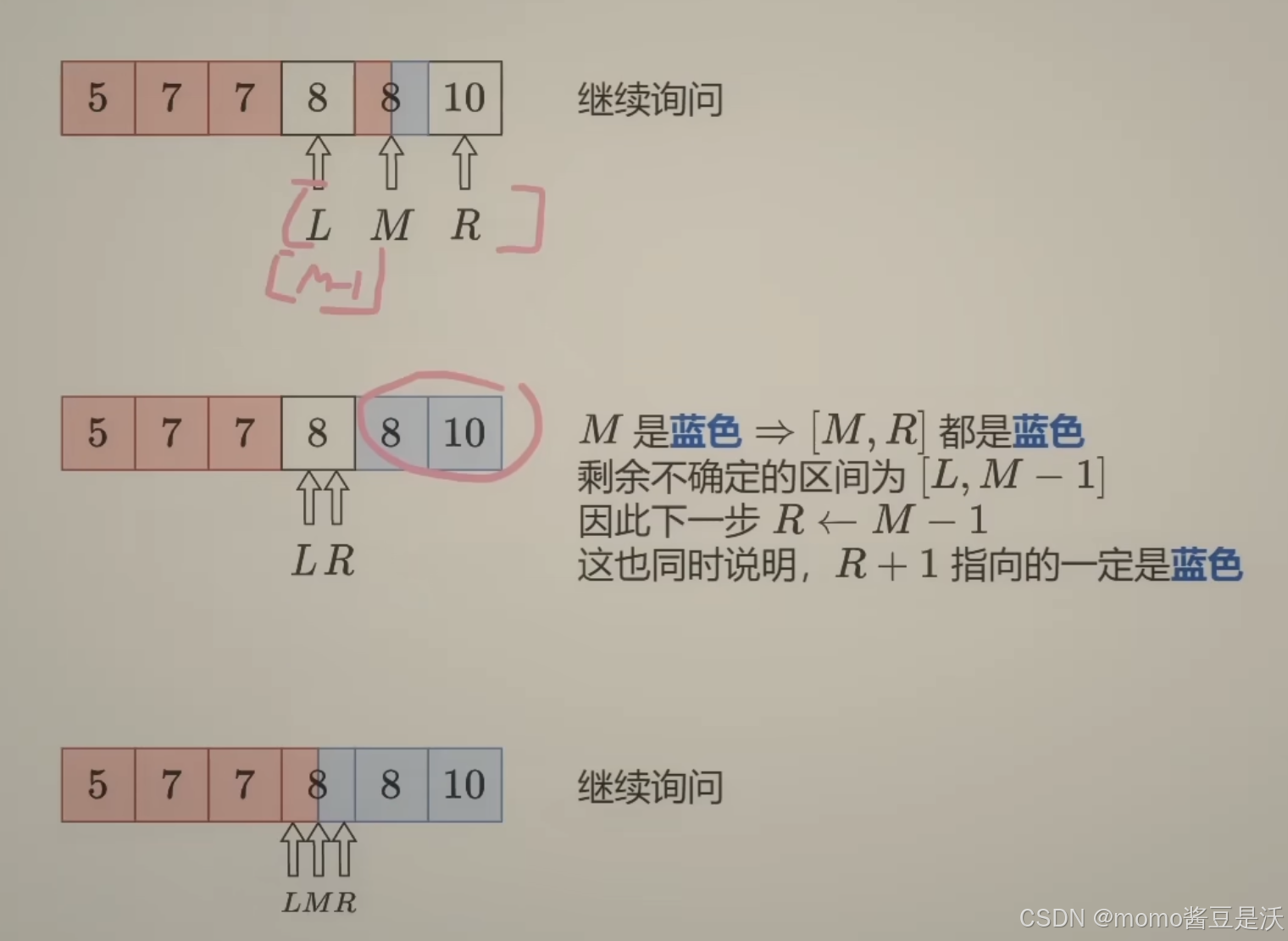
关键：🔴牢牢记住这个区间的定义，是解题的关键！【补充】理解二分，请牢记区间的定义！区间内的数（下标）都是还未确定与 target 的大小关系的，有的是 < target，有的是 ≥ target；区间外的数（下标）都是确定与 target 的大小关系的。

代码

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int start = lowerBound(nums, target);
        if (start == nums.length || nums[start] != target) {
            return new int[]{-1, -1}; // nums 中没有 target
        }
        // 如果 start 存在，那么 end 必定存在
        int end = lowerBound(nums, target + 1) - 1;
        return new int[]{start, end};
    }

    // lowerBound 返回最小的满足 nums[i] >= target 的下标 i
    // 如果数组为空，或者所有数都 < target，则返回 nums.length
    // 要求 nums 是非递减的，即 nums[i] <= nums[i + 1]
    private int lowerBound(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1; // 闭区间 [left, right]
        while (left <= right) { // 区间不为空
            // 循环不变量：
            // nums[left-1] < target
            // nums[right+1] >= target
            int mid = left + (right - left) / 2;
            if (nums[mid] >= target) {
                right = mid - 1; // 范围缩小到 [left, mid-1]
            } else {
                left = mid + 1; // 范围缩小到 [mid+1, right]
            }
        }
        // 循环结束后 left = right+1
        // 此时 nums[left-1] < target 而 nums[left] = nums[right+1] >= target
        // 所以 left 就是第一个 >= target 的元素下标
        return left;
    }
}

左闭右开区间写法

代码

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int start = lowerBound(nums, target);
        if (start == nums.length || nums[start] != target) {
            return new int[]{-1, -1}; // nums 中没有 target
        }
        // 如果 start 存在，那么 end 必定存在
        int end = lowerBound(nums, target + 1) - 1;
        return new int[]{start, end};
    }

    // lowerBound 返回最小的满足 nums[i] >= target 的下标 i
    // 如果数组为空，或者所有数都 < target，则返回 nums.length
    // 要求 nums 是非递减的，即 nums[i] <= nums[i + 1]
    private int lowerBound(int[] nums, int target) {
        int left = 0;
        int right = nums.length; // 左闭右开区间 [left, right)
        while (left < right) { // 区间不为空
            // 循环不变量：
            // nums[left-1] < target
            // nums[right] >= target
            int mid = left + (right - left) / 2;
            if (nums[mid] >= target) {
                right = mid; // 范围缩小到 [left, mid)
            } else {
                left = mid + 1; // 范围缩小到 [mid+1, right)
            }
        }
        // 循环结束后 left = right
        // 此时 nums[left-1] < target 而 nums[left] = nums[right] >= target
        // 所以 left 就是第一个 >= target 的元素下标
        return left;
    }
}

开区间写法（最推荐）

代码

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int start = lowerBound(nums, target);
        if (start == nums.length || nums[start] != target) {
            return new int[]{-1, -1}; // nums 中没有 target
        }
        // 如果 start 存在，那么 end 必定存在
        int end = lowerBound(nums, target + 1) - 1;
        return new int[]{start, end};
    }

    // lowerBound 返回最小的满足 nums[i] >= target 的下标 i
    // 如果数组为空，或者所有数都 < target，则返回 nums.length
    // 要求 nums 是非递减的，即 nums[i] <= nums[i + 1]
    private int lowerBound(int[] nums, int target) {
        int left = -1;
        int right = nums.length; // 开区间 (left, right)
        while (left + 1 < right) { // 区间不为空
            // 循环不变量：
            // nums[left] < target
            // nums[right] >= target
            int mid = left + (right - left) / 2;
            if (nums[mid] >= target) {
                right = mid; // 范围缩小到 (left, mid)
            } else {
                left = mid; // 范围缩小到 (mid, right)
            }
        }
        // 循环结束后 left+1 = right
        // 此时 nums[left] < target 而 nums[right] >= target
        // 所以 right 就是第一个 >= target 的元素下标
        return right;
    }
}

如何处理不是>= 的情况