【LeetCode Solutions】LeetCode 111 ~ 115 题解

LeetCode 111. 二叉树的最小深度（简单）

【题目描述】

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

【示例 1】

输入：root = [3,9,20,null,null,15,7]
输出：2

【示例 2】

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

【提示】

树中节点数的范围在 $[0,10^5]$ 内
$-1000<=Node.val<=1000$

---

【分析】

与 LeetCode 104. 不同的是，如果左右子树中有一个为空，那么只能考虑另一个子树的高度。

因此在递归求解最小高度的时候，如果当前节点是叶子节点（左右子树均为空）则高度为 1，如果当前节点的左右子树都不为空，那么高度为左右子树的最小高度中的较小值加 1，如果只有其中一个子树为空，那么这个空子树的高度可以看成是无穷大。

---

【代码】

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        if (!root) return 0;
        return getMinDepth(root);
    }

    int getMinDepth(TreeNode* root) {
        if (!root) return INT_MAX;
        if (!root->left && !root->right) return 1;
        return min(getMinDepth(root->left), getMinDepth(root->right)) + 1;
    }
};

LeetCode 112. 路径总和（简单）

【题目描述】

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum。判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和 targetSum。如果存在，返回 true；否则，返回 false。

叶子节点是指没有子节点的节点。

【示例 1】

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

【示例 2】

输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

【示例 3】

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

【提示】

树中节点的数目在范围 $[0,5000]$ 内
$-1000<=Node.val<=1000$
$-1000<=targetSum<=1000$

---

【分析】

本题也是自上而下考虑，记录从根节点下来走到每个节点时的总和，具体实现可以在递归函数中传入一个参数 sum 表示走到当前节点之前的路径上所有节点值之和是多少，如果当前节点是叶子节点且 sum 加上当前节点的值恰好等于 targetSum 则返回 true。

我们也可以在每次往下走的时候将 targetSum 减去当前节点的值，这样如果某个叶子节点的值恰好等于 targetSum 也就说明从根节点走到该节点的路径之和恰好等于 targetSum。

---

【代码】

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if (!root) return false;
        if (!root->left && !root->right && root->val == targetSum) return true;
        return hasPathSum(root->left, targetSum - root->val) || hasPathSum(root->right, targetSum - root->val);
    }
};

LeetCode 113. 路径总和 II（中等）

【题目描述】

给你二叉树的根节点 root 和一个整数目标和 targetSum，找出所有从根节点到叶子节点路径总和等于给定目标和的路径。

叶子节点是指没有子节点的节点。

【示例 1】

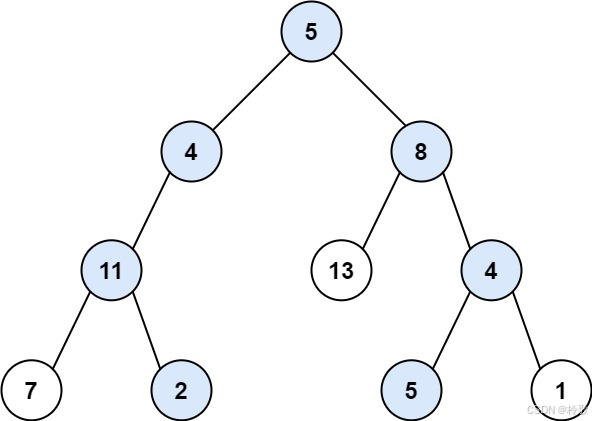
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

【示例 2】

输入：root = [1,2,3], targetSum = 5
输出：[]

【示例 3】

输入：root = [1,2], targetSum = 0
输出：[]

【提示】

树中节点的数目在范围 $[0,5000]$ 内
$-1000<=Node.val<=1000$
$-1000<=targetSum<=1000$

---

【分析】

本题和上一题一样，只是需要将路径记录下来，并且无论其中一个子树是否存在答案都需要遍历另一个子树，因为要搜索出所有符合要求的路径。

---

【代码】

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> res;

    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        dfs(root, targetSum, vector<int>{});
        return res;
    }

    void dfs(TreeNode* root, int sum, vector<int> v) {
        if (!root) return;
        v.push_back(root->val);
        if (!root->left && !root->right && root->val == sum) {
            res.push_back(v);
        } else {
            dfs(root->left, sum - root->val, v);
            dfs(root->right, sum - root->val, v);
        }
        v.pop_back();
    }
};

LeetCode 114. 二叉树展开为链表（中等）

【题目描述】

给你二叉树的根结点 root，请你将它展开为一个单链表：

• 展开后的单链表应该同样使用 TreeNode，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null。
• 展开后的单链表应该与二叉树先序遍历顺序相同。

【示例 1】

输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

【示例 2】

输入：root = []
输出：[]

【示例 3】

输入：root = [0]
输出：[0]

【提示】

树中结点数在范围 $[0,2000]$ 内
$-100<=Node.val<=100$

进阶：你可以使用原地算法（即 $O(1)$ 额外空间）展开这棵树吗？

---

【分析】

对于某个节点，我们分以下两种情况处理：

• 存在左子树：将左子树插入到当前节点的右边，然后遍历到右儿子；
• 不存在左子树：直接遍历到右儿子。

将左子树插入到右侧其实就是先找到当前点 cur 的前驱节点 p（其左子树靠右侧的最后一个节点），然后进行以下更新：

• p->right = cur->right；
• cur->right = cur->left；
• cur->left = nullptr。

画个图来理解一下：

---

【代码】

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void flatten(TreeNode* root) {
        while (root) {
            if (root->left) {
                TreeNode* p = root->left;
                while (p->right) p = p->right;  // 找到前驱节点
                p->right = root->right;  // 更新前驱节点的右儿子
                root->right = root->left;  // 更新当前节点的右儿子
                root->left = nullptr;  // 将当前节点的左儿子置为空
            }
            root = root->right;
        }
    }
};

LeetCode 115. 不同的子序列（困难）

【题目描述】

给你两个字符串 s 和 t，统计并返回在 s 的子序列中 t 出现的个数，结果需要对 $10^9+7$ 取模。

【示例 1】

输入：s = "rabbbit", t = "rabbit"
输出：3
解释：
如下所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
[rabb]b[it]
[rab]b[bit]
[ra]b[bbit]

【示例 2】

输入：s = "babgbag", t = "bag"
输出：5
解释：
如下所示, 有 5 种可以从 s 中得到 "bag" 的方案。 
[b]abgb[ag]
[ba]b[g]bag
[ba]bgba[g]
ba[b]gb[ag]
babg[bag]

【提示】

$1<=s.length,t.length<=1000$
s 和 t 由英文字母组成

---

【分析】

看到两个字符串求方案数的这类问题一般就会联想到动态规划：

• 状态表示：$f[i][j]$ 表示 s[1, i] 的所有与 t[1, j] 相等的子序列的数量。
• 状态计算
  • 子序列中不包含 s[i]：这种情况无需满足任何条件，无论 s[i] 是否等于 t[j] 都可以不包含 s[i]，这种情况下的数量为 s[1, i - 1] 中所有与 t[1, j] 相等的子序列数量，即 f[i][j] = f[i - 1][j]；
  • 子序列中包含 s[i]：首先需要满足条件 s[i] == t[j]，这种情况下的数量为 s[1, i - 1] 中所有与 t[1, j - 1] 相等的子序列数量，即 f[i][j] = f[i - 1][j - 1]。

如果 t 为空，那么任意长度的 s 都有一种与 t 相等的子序列，也就是同样为空串，即初始化：f[0 ~ s.size()][0] = 1。

---

【代码】

class Solution {
public:
    int numDistinct(string s, string t) {
        int n = s.size(), m = t.size();
        s = ' ' + s, t = ' ' + t;
        vector<vector<int>> f(n + 1, vector<int>(m + 1));
        for (int i = 0; i <= n; i++) f[i][0] = 1;
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++) {
                f[i][j] = f[i - 1][j];
                if (s[i] == t[j]) f[i][j] = (f[i][j] + f[i - 1][j - 1]) % int(1e9 + 7);
            }
        return f[n][m];
    }
};