企业网站的设计怎么做路由硬盘做网站空间不

Educational Codeforces Round 174 (Rated for Div. 2) C. Beautiful Sequence

这道题真是赛时不知道怎么推，赛后一看题解就觉得自己是个XX。

• 知识点：思维，递推

简单来讲就是要求一下形如 1 2 2 2 … 2 3 这样的子序列的个数。

考虑线性递推：f[i][1, 2, 3] 表示以第i个数字结尾的，且a[i] = 1, 2, 3 的满足条件的序列数；
这里对状态方程的定义有点模糊，因为这里严格来讲不太像DP，更像是一种递推。

看一下转移，首先借助前缀和的思想，f[i] = f[i - 1]，三个状态的数量都等于上一步的数量，再加上这一步的贡献。

• 对于a[i] == 1;
  f[i][1] += 1;
• 对于a[i] == 2;
  f[i][2] += f[i - 1][2];
  // 可以看作这个2可以加在之前任何一个以2结尾的序列的末尾，所以就是加上之前所有的。
  f[i][2] += f[i - 1][1];
  // 也可以是直接接在之前任何一个1的末尾，所以加上1的数量。
• 对于a[i] == 3;
  f[i][3] += f[i][2];
  就是答案。

#include<bits/stdc++.h>using namespace std;
using i64 = long long;
using u64 = unsigned long long;#define int long long
#define debug(x) cerr << #x" = " << x << '\n';typedef pair<int, int> PII;const i64 N = 2e5 + 10, INF = 1e18 + 10;int mod = 998244353;void solve()
{int n;cin >> n;vector<int> a(n + 1);for (int i = 1; i <= n; i++) {cin >> a[i];}vector<int> f(4, 0);for (int i = 1; i <= n; i++) {if (a[i] == 1) {(f[1] += 1) %= mod;} else if (a[i] == 2) {(f[2] += f[2]) %= mod;(f[2] += f[1]) %= mod;} else if (a[i] == 3) {(f[3] += f[2]) %= mod;}}cout << f[3] % mod << endl;
}signed main()
{cin.tie(0) -> ios::sync_with_stdio(false);int T = 1;cin >> T;while (T --) solve();return 0;
}

这里其实不难发现每一次f 都是由 i - 1转移过来，所以可以直接省去一维。

Codeforces Round 903 (Div. 3) E. Block Sequence

• 知识点：线性DP，正难则反

首先考虑正向转移，设状态表示为 f[i] 表示 从 1 ~ i 这段为完美序列的最小的修改次数

但是这里就遇到了一个问题，对于一个数字 a[i] 它是向 i 后面的某个位置转移的，这样就很难写出转移方程。

所以这里要想到从后向前转移，f[i] 表示 从 i ~ n 这段为完美序列的最小的修改次数

转移方程就很简单了，从后向前遍历，f[i] 要不是从 f[i + 1] 转移过来，要不就是从 f[i + a[i] + 1] 转移过来。

#include<bits/stdc++.h>using namespace std;
using i64 = long long;
using u64 = unsigned long long;#define int long long
#define debug(x) cerr << #x" = " << x << '\n';typedef pair<int, int> PII;const i64 N = 2e5 + 10, INF = 1e18 + 10;int mod;void solve()
{int n;cin >> n;vector<int> a(n + 1);for (int i = 1; i <= n; i++) {cin >> a[i];}vector<int> f(n + 2, 0);f[n] = 1;for (int i = n - 1; i >= 1; i--) {f[i] = f[i + 1] + 1;if (i + a[i] <= n) f[i] = min(f[i], f[i + a[i] + 1]);}cout << f[1] << endl;
}signed main()
{cin.tie(nullptr) -> ios::sync_with_stdio(false);int T = 1;cin >> T;while (T --) solve();return 0;
}

Codeforces Round 978 (Div. 2) C. Gerrymandering

• 知识点：状态机 + 线性递推

为数不多的一遍过的DP

初看题目很复杂，不知道怎么写状态方程，手玩了几个样例就可以发现一个结论，那就是无论怎么划分，都可以看作是类似若干个以下这种状态拼在一起。

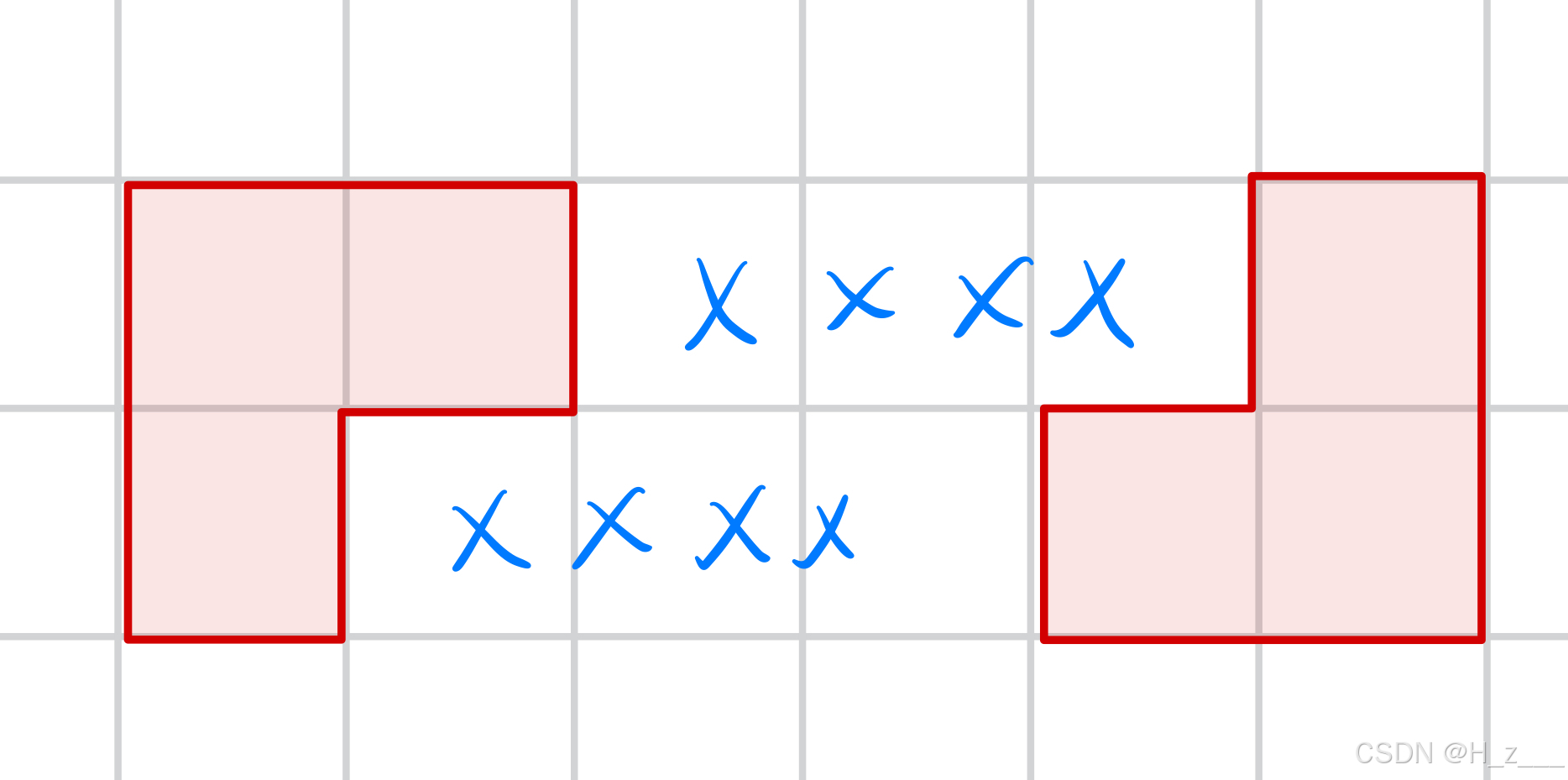
而且我们还发现，将整个数组划分为三列三列的，每三列的情况都是可以重复：

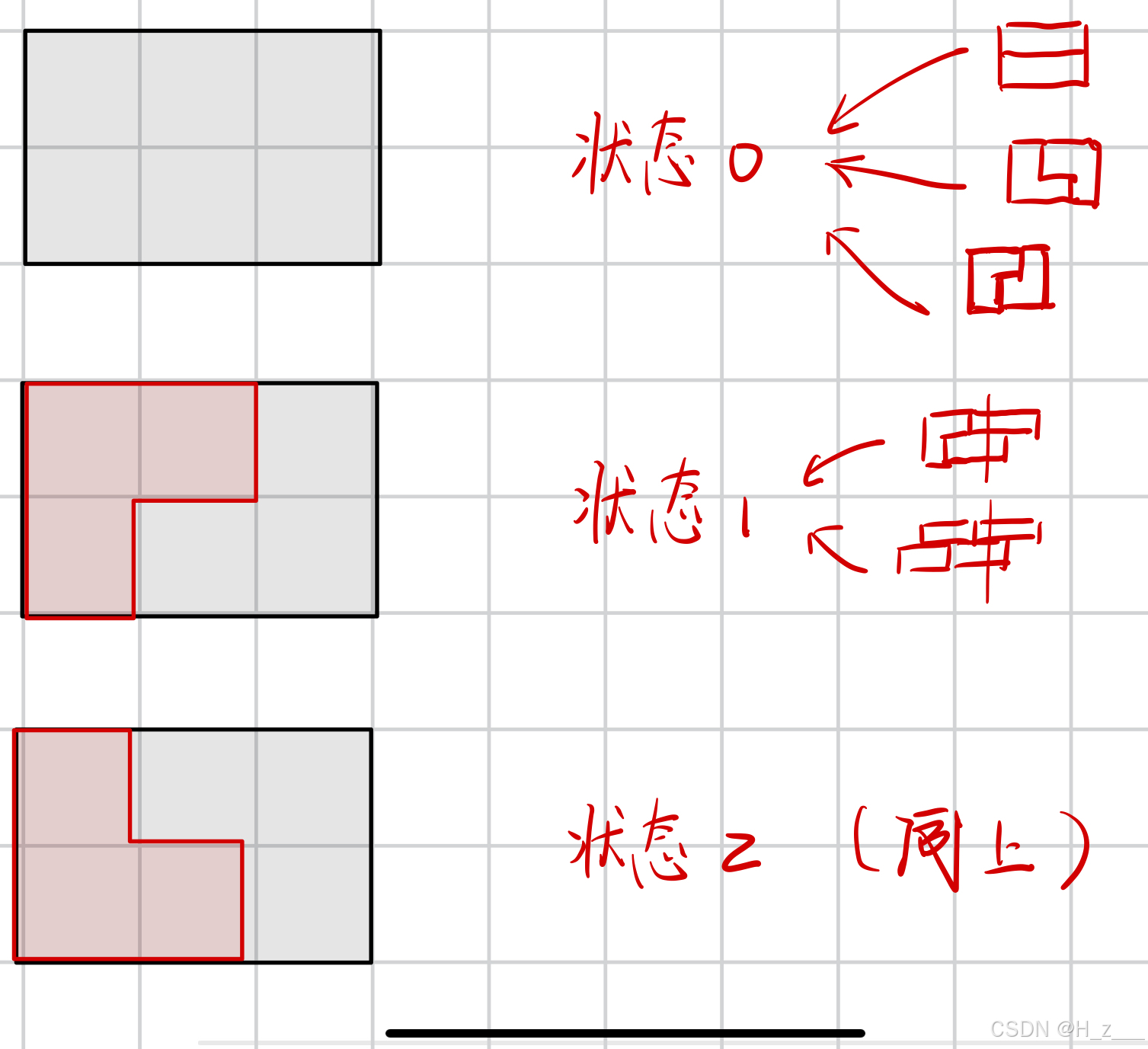
所以我们就可以对每三列列状态方程：
f[i][0, 1, 2] 表示，第i个三列，且第i + 1个三列的状态是 0 1 2 的票数最大值

然后我们就可以进行转移了，但是转移的方程非常不好写，要讨论很多块拼在一起的情况，我们对所有能划分成的块分为10种：

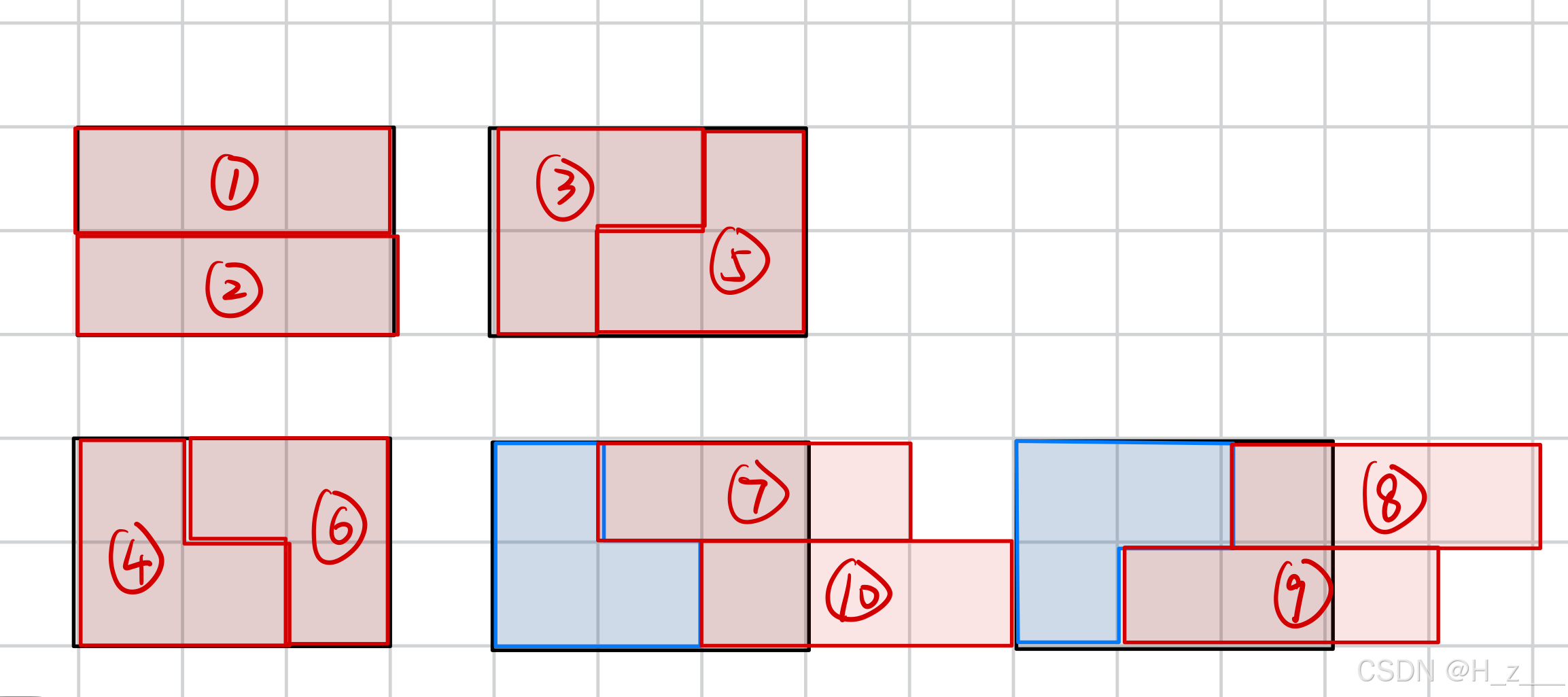
统计每种能产生1还是0的贡献，然后再由上图转移方程进行转移。

参考代码如下：（计算10个块的贡献我写的太麻烦了，大家知道意思就行）

void solve()
{int n;cin >> n;vector<string> g(3);for (int i = 1; i <= 2; i++) cin >> g[i], g[i] = ' ' + g[i]; vector<vector<int>> f(n + 1, vector<int>(3, -INF));f[0][0] = 0;for (int i = 1; i <= n / 3; i++) {int j = (i - 1) * 3 + 1;vector<int> block(11, 0);for (int x = j; x <= j + 2; x++) {block[1] += (g[1][x] == 'A') - (g[1][x] == 'J');block[2] += (g[2][x] == 'A') - (g[2][x] == 'J');}block[3] += (g[1][j] == 'A') - (g[1][j] == 'J') + (g[2][j] == 'A') - (g[2][j] == 'J') + (g[1][j + 1] == 'A') - (g[1][j + 1] == 'J');block[4] += (g[1][j] == 'A') - (g[1][j] == 'J') + (g[2][j] == 'A') - (g[2][j] == 'J') + (g[2][j + 1] == 'A') - (g[2][j + 1] == 'J');block[5] += (g[1][j + 2] == 'A') - (g[1][j + 2] == 'J') + (g[2][j + 2] == 'A') - (g[2][j + 2] == 'J') + (g[2][j + 1] == 'A') - (g[2][j + 1] == 'J');block[6] += (g[1][j + 2] == 'A') - (g[1][j + 2] == 'J') + (g[2][j + 2] == 'A') - (g[2][j + 2] == 'J') + (g[1][j + 1] == 'A') - (g[1][j + 1] == 'J');if (i != n / 3) {for (int x = j + 1; x <= j + 3; x++) {block[7] += (g[1][x] == 'A') - (g[1][x] == 'J');block[9] += (g[2][x] == 'A') - (g[2][x] == 'J');}for (int x = j + 2; x <= j + 4; x++) {block[8] += (g[1][x] == 'A') - (g[1][x] == 'J');block[10] += (g[2][x] == 'A') - (g[2][x] == 'J');}}for (int i = 1; i <= 10; i++) block[i] = (block[i] >= 1) ? 1 : 0;f[i][0] = max({f[i - 1][0] + max({block[1] + block[2], block[3] + block[5], block[4] + block[6]}), f[i - 1][1] + block[5], f[i - 1][2] + block[6]});if (i != n / 3) {f[i][1] = max({f[i - 1][1] + block[8] + block[9], f[i - 1][0] + block[3] + block[8] + block[9]});f[i][2] = max({f[i - 1][2] + block[7] + block[10], f[i - 1][0] + block[4] + block[7] + block[10]});}}cout << f[n / 3][0] << endl;return;
}

Codeforces Beta Round 89 (Div. 2) D. Caesar’s Legions

• 知识点：连续不超过若干个数字的处理方式

针对这种连续不超过多少个数字的状态我们一般有两种应对措施：

• 直接在状态表示中表示出来，也就是记录下连续多少个的状态
• 转移的时候只从某个范围进行转移，保证不超过最大限制

接下来，我们从这两个角度来写一下这道题：

状态可以设为 $f[i][j][k_1][k_2]$ 一共i个步兵以及j个骑兵且步兵在末尾连续放了k1个，而骑兵在末尾连续放了k2个。

我们设状态转移方程为

• $f[i][j][k_1][k_2]=f[i-1][j][k_1-1][0]$；
• $f[i][j][k_1][k_2]=f[i][j-1][0][k_2-1]$；
• $f[i][j][0][1]=f[i][j-1][k_1][0]$ 也就是可以由任何结尾数量转化为另一种数量为1，这种数量为0的情况；
• $f[i][j][1][0]=f[i-1][j][0][k_2]$；

注意初始化，不然会WA

void solve()
{int n1, n2, k1, k2;cin >> n1 >> n2 >> k1 >> k2;f[1][0][1][0] = f[0][1][0][1] = 1;for (int i = 2; i <= min(k1, n1); i++) {(f[i][0][i][0] = f[i - 1][0][i - 1][0]) %= mod;}for (int i = 2; i <= min(k2, n2); i++) {(f[0][i][0][i] = f[0][i - 1][0][i - 1]) %= mod;}for (int i = 1; i <= n1; i++) {for (int j = 1; j <= n2; j++) {for (int k = 1; k <= min(i, k1); k++) {(f[i][j][k][0] += f[i - 1][j][max(k - 1, 0LL)][0]) %= mod;(f[i][j][0][1] += f[i][j - 1][k][0]) %= mod;}for (int k = 1; k <= min(j, k2); k++) {(f[i][j][0][k] += f[i][j - 1][0][max(k - 1, 0LL)]) %= mod;(f[i][j][1][0] += f[i - 1][j][0][k]) %= mod;}}}int res = 0;for (int i = 1; i <= min(k1, n1); i++) {(res += f[n1][n2][i][0] % mod) %= mod;}for (int i = 1; i <= min(k2, n2); i++) {(res += f[n1][n2][0][i] % mod) %= mod;}cout << res << endl;}

说实话感觉上述写法不像是正解。。。

再来看另一种状态表示方式

$f[i][j][1/2]$ 表示当前摆了 i 个步兵，j 个骑兵，且当前结尾为 步兵/骑兵 的方案数
状态转移很简单，直接枚举连续的个数然后转移就行。

void solve()
{int n1, n2, k1, k2;cin >> n1 >> n2 >> k1 >> k2;vector<vector<vector<int>>> f(n1 + 1, vector<vector<int>>(n2 + 1, vector<int>(3, 0)));for (int i = 0; i <= min(k1, n1); i++) {f[i][0][1] = 1;}for (int i = 0; i <= min(k2, n2); i++) {f[0][i][2] = 1;}for (int i = 1; i <= n1; i++) {for (int j = 1; j <= n2; j++) {for (int p = 1; p <= min(i, k1); p++) {(f[i][j][1] += f[i - p][j][2]) %= mod;}for (int q = 1; q <= min(k2, j); q++) {(f[i][j][2] += f[i][j - q][1]) %= mod;}}}cout << (f[n1][n2][1] + f[n1][n2][2]) % mod << endl;return;
}

Educational Codeforces Round 150 (Rated for Div. 2) Ranom Numbers

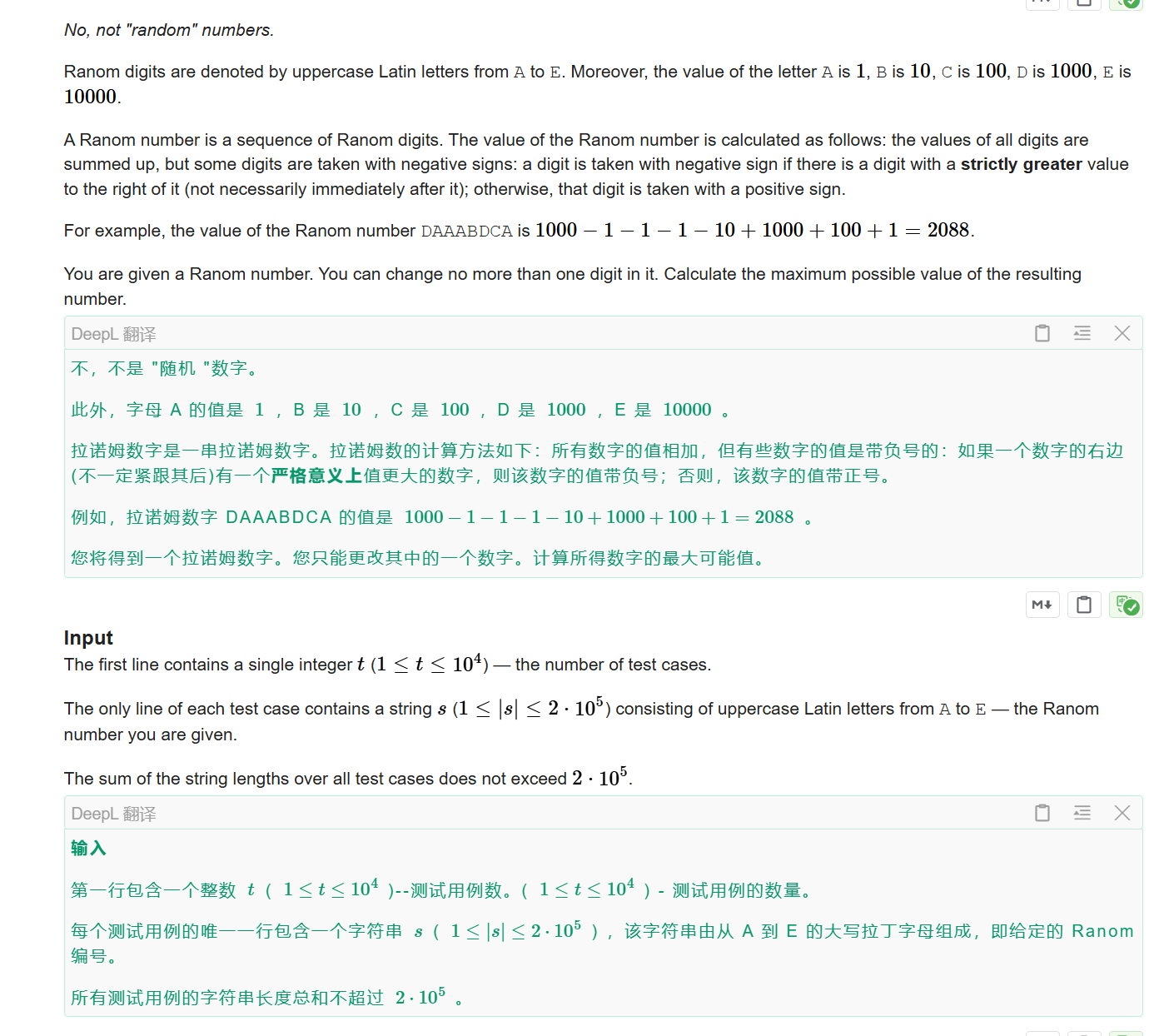
• 知识点：倒叙，状态方程以及转移，状态机

都能看出来是个大模拟，但很难想到状态表示：

$f[i][j][k]$ 表示在 i ~ n 的范围内，目前枚举到了 i 位，且 i + 1 ~ n 这段中的最大的数字是 j，而且目前修改了k（k 只能取 0 / 1）的状态的数字最大值。

所以状态转移就是：

• $f[i][j][k]=f[i+1][y][t]+(+/-)val[j]$

也就是枚举上一位的所有状态，再枚举这一位的所有状态，然后完成转移。
这里注意到可以用滚动数组进行优化，所以可以有如下代码：

int val[] = {1, 10, 100, 1000, 10000};void solve()
{string s;cin >> s;int n = s.size();reverse(s.begin(), s.end());s = ' ' + s;int f[2][5][2];for (int i = 0 ;i < 5; i++) {f[0][i][0] = f[0][i][1] = -INF;}f[0][0][0] = 0;for (int i = 1; i <= n; i++) {for (int j = 0; j < 5; j++) {f[i & 1][j][0] = f[i & 1][j][1] = -INF;}int x = s[i] - 'A';for (int j = 0; j < 5; j++) {  // 枚举的是走到当前位置的最大的数字for (int t = 0; t < 2; t++) {for (int y = 0; y < 5; y++) {int nj = max(j, y);if (t == 1 && x != y) continue;int nt = t + (x != y);f[i & 1][nj][nt] = max(f[i & 1][nj][nt], f[i - 1 & 1][j][t] + (y < nj ? -val[y] : val[y]));}}}}int ans = -INF;for (int i = 0; i < 5; i++) {ans = max({ans, f[n & 1][i][0], f[n & 1][i][1]});}cout << ans << endl;
}

2023 年第五届河南省CCPC 大学生程序设计竞赛 Problem E. 矩阵游戏

• 知识点：二维线性DP，滚动数组优化

一道很经典的DP题目，只是加入了一个x，但是总体思路没有变，只是状态表示多加一维。

$f[i][j][k]$ 表示走到 $(i,j)$ 且替换了 $k$ 个 ？的最大分数；

粗略计算一下空间大概需要开到 $2.5\ast 10^8$，时限两秒勉强卡的过去，只要常数不太大就行，但是空间肯定会爆，所以这里直接滚动数组优化，将层数优化为两层，然后按照奇偶性转移就行。

这里还要注意不要每次都用vector动态分配，不然常数太大会被卡，也不要用 #define int long long

vector<vector<vector<int>>> f(2, vector<vector<int>>(505, vector<int>(1005)));void solve()
{int n, m, x;cin >> n >> m >> x;vector<string> g(n + 1);for (int i = 1; i <= n; i++) {cin >> g[i];g[i] = ' ' + g[i];}for (int i = 0; i <= 1; i++) {for (int j = 0; j <= m; j++) {for (int k = 0; k <= x; k++) {f[i][j][k] = -INF;}}}f[0][1][0] = f[1][0][0] = 0;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {for (int k = 0; k <= x; k++) {if (g[i][j] == '0') {f[i & 1][j][k] = max({f[i - 1 & 1][j][k], f[i & 1][j - 1][k], f[i & 1][j][k]});} else if (g[i][j] == '1') {f[i & 1][j][k] = max({f[i - 1 & 1][j][k] + 1, f[i & 1][j - 1][k] + 1, f[i & 1][j][k]});} else if (g[i][j] == '?') {if (k != 0) f[i & 1][j][k] = max({f[i - 1 & 1][j][k - 1] + 1, f[i - 1 & 1][j][k], f[i & 1][j - 1][k - 1] + 1, f[i & 1][j - 1][k], f[i & 1][j][k]});else f[i & 1][j][k] = max({f[i - 1 & 1][j][k], f[i & 1][j - 1][k], f[i & 1][j][k]});}}}}int ans = -INF;for (int i = 0; i <= x; i++) {ans = max(ans, f[n & 1][m][i]);}cout << ans << endl;
}