当前位置： 首页 > wzjs >正文

网站如何做企业电子宣传册网站建设学什么软件

wzjs 2025/9/6 7:33:17
网站如何做企业电子宣传册,网站建设学什么软件,医疗卫生网站前置审批,抖音是哪家公司开发的软件1.二叉搜索树 1.1二叉搜索树的概念 二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树: 1.若它的左子树不为空，则左子树上所有节点的值都小于根节点的值 2.若它的右子树不为空，则右子树上所有节点的值都…

1.二叉搜索树

1.1二叉搜索树的概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

1.若它的左子树不为空，则左子树上所有节点的值都小于根节点的值

2.若它的右子树不为空，则右子树上所有节点的值都大于根节点的值

3.它的左右子树也分别为二叉搜索树

从上述概念以及图中可以看出，二叉搜索树具有以下特性：

1. 二叉搜索树中最左侧的节点是树中最小的节点，最右侧节点一定是树中最大的节点

2. 采用中序遍历遍历二叉搜索树，可以得到一个有序的序列

1.2二叉树的查找

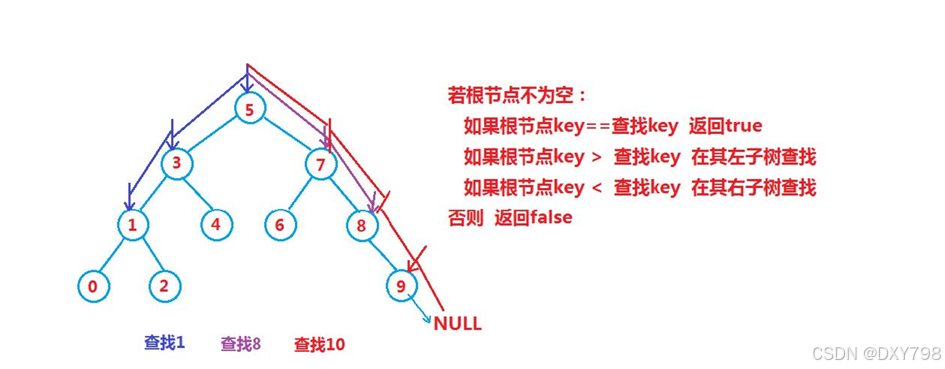
二叉搜索树的性能分析

插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。

对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度 的函数，即结点越深，则比较次数越多。

但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树

最优情况下，二叉搜索树为完全二叉树，其平均比较次数为：\log_{2}N

最差情况下，二叉搜索树退化为单支树，其平均比较次数为：N/2

2.AVL树

AVL树是一颗就对平衡的二叉搜索树，每颗子树的高度差都不超过1，这样可以保证高效的查询--，即\log_{2}N，但是如果要对AVL进行结构上的修改操作，性能是十分的低下，比如在插入时要维护绝对平衡，旋转的次数较多，更差的是删除的时候有可能一直要让旋转持续到根的位置。因此：如果需要 一种查询高效且有序的数据结构，而且数据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修 改，就不太适合。

2.1AVL树的概念

问题：二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺 序表中搜索元素，效率低下。

方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过 1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度

下面这颗AVL树所具有的性质

1.它的左子树和右子树都是AVL树

2.左右子树的高度差（也叫做平衡因子）不会大于2（-1 0 1）

3.如果一颗二叉所搜索树是高度平衡的，那么它就是一颗AVL树，如果这颗·AVL树的节点个数是N的话,那么它的高度为\log_{2}N，搜索时间复杂 度O( \log_{2}N)。

2.2AVL树中的节点定义

当前节点的平衡因子=右子树高度-左子树的高度

2.3AVL树的插入

AVL树的插入又分为两部分 

第一部分：像之前平衡二叉一样插入数据第二部分：平衡因子的调整

插

2.4平衡因子的调整

调整的时候分下面四种情况

2.4.1右单旋

当新节点插入到较高左子树的左侧时--右单旋

 private void rigthrevolve(TreeNode parent, TreeNode cur) {//右旋转的操作和旋左转的差不多TreeNode Pparent=parent.parent;if(cur.rigth!=null){cur.rigth.parent=parent;}parent.left=cur.rigth;parent.parent=cur;cur.rigth=parent;cur.parent=Pparent;cur.bf=0;parent.bf=0;if(parent==root){root=cur;return;}if(cur.val>Pparent.val){//说明parent是Pparent右子树Pparent.rigth=cur;}else{Pparent.left=cur;}}

2.4.2左单旋

当新节点插入到较高右子树的右侧时--左单旋

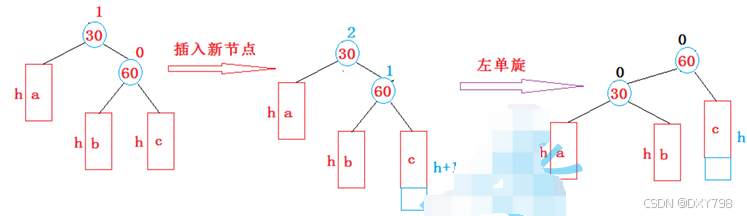
 private void rigthrevolve(TreeNode parent, TreeNode cur) {//右旋转的操作和旋左转的差不多TreeNode Pparent=parent.parent;if(cur.rigth!=null){cur.rigth.parent=parent;}parent.left=cur.rigth;parent.parent=cur;cur.rigth=parent;cur.parent=Pparent;cur.bf=0;parent.bf=0;if(parent==root){root=cur;return;}if(cur.val>Pparent.val){//说明parent是Pparent右子树Pparent.rigth=cur;}else{Pparent.left=cur;}}

2.4.3左右双旋

新节点插入较高左子树的右侧：先左单旋再右单旋 左右双旋

将双旋变成单旋后再旋转，即：先对30进行左单旋，然后再对90进行右单旋，旋转完成后再考虑平衡因子的 更新。

 private void leftrigthrevolve(TreeNode parent, TreeNode cur) {TreeNode PP=parent;TreeNode PL=parent.left;int bbf=cur.rigth.bf;leftrevolve(cur,cur.rigth);rigthrevolve(parent,parent.left);if(bbf==1){cur.bf=-1;}else if(bbf==-1){parent.bf=1;}}

2.4.4右左双旋

新节点插入较高右子树的左侧---右左：先右单旋再左单旋 右左双旋

private void rigthleftrelve(TreeNode parent, TreeNode cur) {TreeNode PP=parent;TreeNode PR=parent.rigth;//这里先要对一个结点的bf值进行存储，用于对不同结构的树的bf赋值int bbf=cur.left.bf;rigthrevolve(cur,cur.left);leftrevolve(parent,parent.rigth);if(bbf==1){parent.bf=-1;}else if(bbf==-1){cur.bf=1;}}

总结：

新插入节点以后，假设pParent为根节点的子树不平衡，即pParent的平衡因子为2或者为-2

1. pParent的平衡因子为2，说明pParent的右子树高，设pParent的右子树的根为pSubR

  当pSubR的平衡因子为1时，执行左单旋

  当pSubR的平衡因子为-1时，执行右左双旋

2. pParent的平衡因子为-2，说明pParent的左子树高，设pParent的左子树的根为pSubL

当pSubL的平衡因子为-1是，执行右单旋

当pSubL的平衡因子为1时，执行左右双旋

即：pParent与其较高子树节点的平衡因子时同号时单旋转，异号时双旋转。

旋转完成后，原pParent为根的子树个高度降低，已经平衡，不需要再向上更新。

2.5AVL树的验证

AVL树的验证需要两点

第一点：证明AVL树是一颗搜索树：使用中序遍历打印，打印出的数据是有序的即可

第二点：验证遍历每个节点，计算每个节点的bf值是否正确

public boolean AVLjudgment(TreeNode cur){if(cur==null){return true;}//验证平衡因子是否正确int rigthheight=height(cur.rigth);int leftheight=height(cur.left);if(rigthheight-leftheight!=cur.bf){System.out.println("平衡因子错误的节点"+cur.val);return false;}return Math.abs(rigthheight-leftheight)<=1&&AVLjudgment(cur.left)&&AVLjudgment(cur.rigth);}//下面是判断这棵树是否是AVL树//1，中序遍历，判断顺序,只能判断是否是平衡树public void middletraverse(TreeNode cur){if(cur==null){return;}System.out.println(" "+cur.val);middletraverse(cur.left);middletraverse(cur.rigth);}//2，计算高度，验证计算的bf是否是正确的public int height(TreeNode cur){if(cur==null){return 0;}int leftheight=height(cur.left);int rigthheight=height(cur.rigth);return leftheight>rigthheight?leftheight+1:rigthheight+1;}

3.红黑树

红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O(\log_{2}N )，红黑树不追求绝对平衡，其只需保 证最长路径不超过最短路径的2倍，相对而言，降低了插入和旋转的次数，所以在经常进行增删的结构中性能比 AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多。

3.1红黑树的概念

红黑树是一种二叉搜索树， 但在每个节点上增加一个成员变量用于储存每个节点的颜色，颜色可以是RED，BLECK通过对任何 一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近 平衡的。

红黑树的性质：

1.每个节点的颜色不是黑色就是红色

2.根节点是黑色

3.不可以有两个连续的两个红色节点

4.每条路径的黑色节点个数是一样的

3.2红黑树结点的定义

3.3红黑树的插入

红黑树的插入也是分成两部分

1. 按照二叉搜索的树规则插入新节点

2. 检测新节点插入后，红黑树的性质是否造到破坏 因为新节点的默认颜色是红色，因此：如果其双亲节点的颜色是黑色，没有违反红黑树任何性质，则不需要 调整；但当新插入节点的双亲节点颜色为红色时，就违反了性质不能有连在一起的红色节点，

此时需要对 红黑树分情况来讨论：

                   约定:cur为当前节点，p为父节点，g为祖父节点，u为叔叔节点

情况一: cur为红，p为红，g为黑，u存在且为红

                 注意：此时看到的树可能是一颗子树也有可能是一颗完整的树

如果g是根节点，只需要将根节点这个节点的是颜色改成黑色即可

如果g不是根节点，如果g这个节点的双亲结点的是红色的话，就需要继续向上调整

情况二: cur为红，p为红，g为黑，u不存在/u为黑

p为g的左孩子，cur为p的左孩子，则进行右单旋转；

相反， p为g的右孩子，cur为p的右孩子，则进行左单旋转

p、g变色--p变黑，g变红

  说明：u有两种情况

1.如果u这个节点不存在的话，则cur肯定是一个新插入的节点，

如果cur不是新插入的节点，则cur和parent节点一定有一个节点是黑色的，

这样的话就不满足性质每条路径上的黑色节点都是相同的

2.如果u这个节点存在的话，则其颜色一定是黑色的，那么cur这个节点原来的颜色一定是黑色的，现在看见是红色的样子是因为想上那个调整，将cur这个节点的颜色改成了红色


 

情况三: cur为红，p为红，g为黑，u不存在/u为黑

p为g的左孩子，cur为p的右孩子，则针对p做左单旋转；

相反， p为g的右孩子，cur为p的左孩子，则针对p做右单旋转

则转换成了情况2

 //第二步：对接点对红黑树节点的颜色和位置进行调整//只有parent存在并且颜色是红色的话就需要进行调整while(parent!=null&&parent.color==Color.RED){//一轮循环结束以后都需要将根节点的颜色手动置为黑色//根据标准：根节点一定是黑色的，所以parent一定不是根节点RBTreeNode  GrandFather =parent.parent;RBTreeNode Uncle=null;if(GrandFather.left==parent){//双亲节点在左边Uncle=GrandFather.rigth;}else{//反之Uncle=GrandFather.left;}//情况一: cur为红，p为红，g为黑，u存在且为红if(Uncle!=null&&Uncle.color==Color.RED){//像这种情况cur节点都是新插入进去的，而且，cur无论是插入在哪个叶子节点的位置，操作都是一样的parent.color=Color.BLACK;Uncle.color=Color.BLACK;//然后该改变祖父节点，祖父节点上面的节点有三种情况，第一种祖父节点就是根节点，// 第二种祖父上面是黑色节点，第三种祖父节点上面是红色节点，（但都是将祖父节点改成红色）GrandFather.color=Color.RED;//继续向上调整cur=GrandFather;parent=GrandFather.parent;root.color=Color.BLACK;continue;}//情况二: cur为红，p为红，g为黑，u不存在/u为黑if(Uncle==null||Uncle.color==Color.BLACK){//情况三：这种情况就是位置不一样,就先将情况三变成情况情况二if(parent==GrandFather.left&&cur==parent.rigth){leftrevolve(parent,cur);RBTreeNode node1=cur;cur=parent;parent=node1;}else if(parent==GrandFather.rigth&&cur==parent.left){rigthrevolve(parent,cur);RBTreeNode node1=cur;cur=parent;parent=node1;}if(cur==parent.left&&parent==GrandFather.left){//使用右旋rigthrevolve(GrandFather,parent);}else if(cur==parent.rigth&&parent==GrandFather.rigth){//使用左旋leftrevolve(GrandFather,parent);}//在对颜色进行改变parent.color=Color.BLACK;GrandFather.color=Color.RED;root.color=Color.BLACK;break;//因为根节点变成了继parent，parent的颜色为黑色所以没有必要继续向上调整}}return true;

3.4红黑树的验证

红黑树的验证也是分成两部分

1.验证红黑树是一颗二叉搜索树

 public void inorder(RBTreeNode cur){if(cur==null){return;}inorder(cur.left);System.out.println(cur.val+" ");inorder(cur.rigth);}

2.验证红黑树是否满足各个性质

 //第二步，满足下面几个性质//   2. 每个结点不是红色就是黑色// 3. 根节点是黑色的// 4. 如果一个节点是红色的，则它的两个孩子结点是黑色的【没有2个连续的红色节点】//  5. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均 包含相同数目的黑色结点public boolean  isRBTreeNode (RBTreeNode root){//如果根节点为空，也是一棵红黑树if(root==null){return true;}if(root.color!=Color.BLACK){System.out.println("违反了性质三：根节点不是黑色");return false;}//先进行统计其中一条路径中的黑色节点数RBTreeNode cur=root;int BlackTreeNode =0;while(cur!=null){if(cur.color==Color.BLACK){BlackTreeNode++;}cur=cur.left;}return  checkRedTreeNode(root)&& checkBlackTreeNode(0,BlackTreeNode,root);}/*** //用于验证性质：对于每个结点，从该结点到其所有后代叶结点的简单路径上，均 包含相同数目的黑色结点* @param newbleck :表示的是当前黑色节点的个数* @param BlackTreeNode；表示每条路径黑色节点的个数* @param cur* @return*/public boolean checkBlackTreeNode(int newbleck,int BlackTreeNode,RBTreeNode cur){if(cur.color==Color.BLACK){newbleck++;}if(cur.left==null&&cur.rigth==null){if(newbleck!=BlackTreeNode){System.out.println("违反了性质：每条路径上黑色节点的个数是一样的");return false;}return true;}return checkBlackTreeNode(newbleck, BlackTreeNode, cur.left)&&checkBlackTreeNode(newbleck, BlackTreeNode, cur.rigth);}/*** 用于验证性质： 如果一个节点是红色的，则它的两个孩子结点是黑色的【没有2个连续的红色节点】* @param cur* @return*/public boolean checkRedTreeNode (RBTreeNode cur){if(cur==null){return true;}if(cur.color==Color.RED){if(cur.parent!=null&&cur.parent.color==Color.RED){System.out.println("违反了性质四：连续出现了两个红色节点");return false;}}return checkRedTreeNode(cur.left)&& checkRedTreeNode(cur.rigth);}

文章转载自：

http://AYTTqoJP.pwbps.cn
http://XVGNO2u7.pwbps.cn
http://cvTARZCb.pwbps.cn
http://habfE0MI.pwbps.cn
http://0BwWhgC8.pwbps.cn
http://UTXD3Jbl.pwbps.cn
http://8RnkgvWB.pwbps.cn
http://AU3Gzsir.pwbps.cn
http://oIgznvUi.pwbps.cn
http://K74454lP.pwbps.cn
http://tsvJLKvO.pwbps.cn
http://16MMN0jt.pwbps.cn
http://fZrOQJq9.pwbps.cn
http://LbdBxoC3.pwbps.cn
http://tK7obfSr.pwbps.cn
http://DgfUfjJ0.pwbps.cn
http://M40lKiIq.pwbps.cn
http://FN1giIeJ.pwbps.cn
http://R1VAIVOe.pwbps.cn
http://06IT4YkE.pwbps.cn
http://lRUwI6At.pwbps.cn
http://3axc41i2.pwbps.cn
http://hFIgOas3.pwbps.cn
http://VIJ0ryKt.pwbps.cn
http://IQL1lzNd.pwbps.cn
http://K4HnCXKt.pwbps.cn
http://aha9pPEf.pwbps.cn
http://zDqbbVuu.pwbps.cn
http://WJF8jmw5.pwbps.cn
http://LE73LF5E.pwbps.cn
http://www.dtcms.com/wzjs/627989.html

相关文章：

  • 如何做好一个网站运营动漫设计培训机构哪里好
  • 廊坊做网站外包做的比较好的二手交易网站
  • 织梦网站2个模型c 做网站怎么连接到别的网页
  • 网站建设排名公司做像美团淘宝平台网站多少钱
  • 飞数石家庄网站建设深圳市住房和建设局网站和市住宅租赁管理服务中心
  • 赣州网站建设平台外包小程序开发注意事项
  • 如何自己建造网站免费网页设计生成器
  • 网站如何做app广东做网站找谁
  • wordpress网站域名地址物流网络名词解释
  • 云南电信网站备案北京工商注册网官网
  • 网站推广方案注意事项网络营销的概念与含义谷歌
  • 注销网站备案时间wordpress icp
  • 门户网站程序做网站公司需要帮客户承担广告法吗
  • 怎么做彩票网站做网站平台公司有哪些
  • wordpress博客站搭建怎么做培训班网站
  • 宁波企业网站开发com网站域名注册
  • 建设品牌网站免费合作加工厂
  • 线上学编程哪个机构比较好四川seo推广公司
  • 电商网站建设资讯子夜免费观看
  • 海淀区网站建设公司广州网站建设定制费用
  • php程序员湛江seo网站管理
  • 国内公司网站需要备案吗烟台seo网站推广费用
  • 怎么自己创建网站免费wordpress系统配置
  • 深圳市建设注册执业资格中心网站网站代理做反向
  • 做网站的好公司有哪些网站建设 天猫 保证金
  • 基本型电子商务网站2019河北省建设厅检测员报名网站
  • 哪个网站可以免费学编程做网站策划书
  • ui外包网站网站域名空间购买
  • 手机建站平台哪个便宜查公司注册信息怎么查
  • 网站建设哪家学校好apache 静态网站