东莞网站开发公司哪家好自己有网站做app吗

一、AVL树

        AVL树也就是二叉平衡树，首先需要满足二叉搜索树的要求，也就是，左子树的值小于根值小于右子树的值，同时，所有子树也满足要求。

        但是由于二叉搜索树并不能总是达到理想状态——完全二叉树或者满二叉树，从而使得查找效率达不到o(logN)。

        AVL树由此而来，之所以被叫做平衡树，是因为要保持树的平衡因子——右子树高度减去左子树高度，使平衡因子的绝对值小于等于一。同时，树的所有子树也要满足平衡的要求。

        通过平衡的办法，就能使得树保持一个相对理想的状态，使搜索效率大大提升。

二、实现

2.1结点内容

        由于新增了平衡因子，且在插入后，需要根据平衡因子去对树的结构进行调整并向上传递，例如：

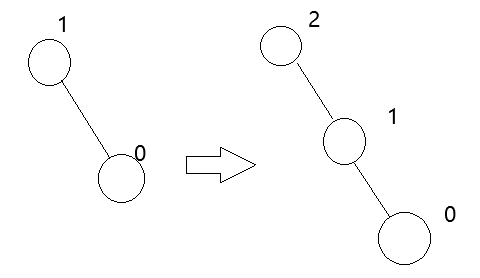
        在图中插入一个结点以后，父结点的平衡因子需要修改，并且父结点平衡因子的修改，也需要向上传递。因此，结点内还需要保存父结点的指针。

template<class T>
struct AVLTreeNode
{AVLTreeNode(const T& data = T()): _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr), _data(data), _bf(0){}AVLTreeNode<T>* _pLeft;AVLTreeNode<T>* _pRight;AVLTreeNode<T>* _pParent;T _data;int _bf;   // 节点的平衡因子
};

        这就是树结点的内容。

2.2平衡因子的传递与修改

 

        还是这个图，在插入一个结点以后，平衡因子是如何进行传递和修改的呢？

        首先我们需要回到平衡因子的定义，也就是右子树高度减去左子树的高度。那么，如果插入的结点在父结点的右子树，父结点的平衡因子就加一，相反插入在父结点的左子树，父结点的平衡因子减一，那么插入结点父结点的平衡因子就修改完成。

        父结点平衡因子修改完成以后，什么情况需要向上传递呢？

• 父结点平衡因子为0时，证明修改前后，树的高度无变化，不需要向上传递
• 父结点平衡因子的绝对值为1时，说明修改前后，树的高度增加1，因此需要向上传递。向上传递时，需要将父结点当做新插入的子结点去修改父结点的父结点，也就是，如果父结点在父结点的父结点的右子树时，父结点的父结点平衡因子加一，相反则减一。
• 父结点平衡因子绝对值为2时，说明修改前后，树的高度增加1。但是，此时，以父结点为根结点的子树已经不满足平衡二叉树的要求，因此需要通过旋转来调整。

        旋转的部分可以先按下不表，我们可以先将插入和修改平衡因子的部分实现：

bool Insert(const T& data) {if (_pRoot == nullptr) {_pRoot = new Node(data);return true;}Node* cur = _pRoot;Node* parent = nullptr;while (cur) {parent = cur;if (cur->_data < data) {cur = cur->_pRight;}else if (cur->_data > data) {cur = cur->_pLeft;}else {return false;}}cur = new Node(data);cur->_pParent = parent;if (parent->_data > data) {parent->_pLeft = cur;}else {parent->_pRight = cur;}while (parent) {if (cur == parent->_pLeft) {parent->_bf--;}else {parent->_bf++;}if (parent->_bf == 0) break;if (abs(parent->_bf) == 1) {cur = parent;parent = parent->_pParent;continue;}else if (abs(parent->_bf) == 2) {//旋转break;}else {assert(false);}}while (parent != nullptr && parent->_pParent != nullptr) {parent = parent->_pParent;}_pRoot = parent;return true;
}

        到这里，除开旋转，插入的主体已经被实现出来。

2.3平衡二叉树的旋转

        旋转需要考虑的情况比较多，但是可以被抽象成为四种情况：

2.3.1左旋

 

        如图所示，不论h等于多少，最终抽象出来的情况就是图示这样，也就是导致结点平衡因子为2的插入，来自右子树的右子树。即，结点平衡因子为2，插入方向子结点的平衡因子为1。如果是这种情况就需要左旋：

                将b结点的左子树给a，使其成为a的右子树，同时，使a成为b的左子树，b结点的父亲结点变为a结点的父亲结点，由此完成左旋的操作。此时，结点的平衡因子均调整为0，不再需要向上调整平衡因子。

2.3.2右旋

        右旋与左旋相似：

        由于左子树的左子树的插入，导致平衡因子变为-2，即结点平衡因子为-2，插入方向子结点的平衡因子为-1，此时需要右旋。 

        通过右旋，将b结点的右子树给a结点成为a的左子树，然后b成为a的父结点，a的父结点成为b的父结点。最后，平衡因子都化为0，也不需要继续向上迭代。

2.3.3右左旋

        右左旋，即向右旋，再向左旋 ，在遇到如下问题时，单纯的左旋右旋已经无法解决问题，需要对子树进行旋转，转化成上面两种情况，再进行解决：

        插入以后，结点的平衡因子变为2，插入方向的子结点平衡因子为-1，此时，左旋解决不了问题，只能以子结点为基础，进行右旋转化：

 

        经过右旋，使结点平衡因子为2，插入方向子结点平衡因子为-1的情况，转化为可以通过左旋解决的情况。接下来再针对平衡因子为2的结点左旋就可以了：

        需要注意的是，在插入时，插入结点位于子结点的左子结点的左子树还是右子树，会影响到最后调整完成后，左右子结点的平衡因子。 

2.3.4左右旋

        左右旋则是，结点的平衡因子为-2，插入方向的子结点平衡因子为1，此时需要，先对子结点左旋，再针对结点右旋：
 

 2.3.5代码实现

// 右单旋
void RotateR(Node* pParent) {Node* cur = pParent->_pLeft;pParent->_pLeft = cur->_pRight;cur->_pRight = pParent;if (pParent->_pLeft != nullptr) {pParent->_pLeft->_pParent = pParent;}cur->_pParent = pParent->_pParent;pParent->_pParent = cur;if (cur->_pParent != nullptr) {if (cur->_pParent->_pLeft == pParent) {cur->_pParent->_pLeft = cur;}else {cur->_pParent->_pRight = cur;}}cur->_bf = pParent->_bf = 0;
}
// 左单旋
void RotateL(Node* pParent) {Node* cur = pParent->_pRight;pParent->_pRight = cur->_pLeft;cur->_pLeft = pParent;if (pParent->_pRight != nullptr) {pParent->_pRight->_pParent = pParent;}cur->_pParent = pParent->_pParent;pParent->_pParent = cur;if (cur->_pParent != nullptr) {if (cur->_pParent->_pLeft == pParent) {cur->_pParent->_pLeft = cur;}else {cur->_pParent->_pRight = cur;}}cur->_bf = pParent->_bf = 0;
}
// 右左双旋
void RotateRL(Node* pParent) {Node* cur = pParent->_pRight;Node* left = cur->_pLeft;int rl_bf = left->_bf;RotateR(cur);RotateL(pParent);if (rl_bf == 1) {cur->_bf = left->_bf = 0;pParent->_bf = -1;}else {left->_bf = pParent->_bf = 0;cur->_bf = 1;}
}
// 左右双旋
void RotateLR(Node* pParent) {Node* cur = pParent->_pLeft;Node* right = cur->_pRight;int lr_bf = right->_bf;RotateL(cur);RotateR(pParent);if (lr_bf == 1) {right->_bf = pParent->_bf = 0;cur->_bf = -1;}else {cur->_bf = right->_bf = 0;pParent->_bf = 1;}
}

        其中双旋直接复用了单选的函数，但是需要注意的是，平衡因子并不能根据单旋的平衡因子来，需要根据2.3.3所说进行调整，可以参考代码。

2.4插入部分的实现

        这里就可以根据旋转的四种情况，以及判断情况的条件，完整的写出平衡二叉树的插入：

bool Insert(const T& data) {if (_pRoot == nullptr) {_pRoot = new Node(data);return true;}Node* cur = _pRoot;Node* parent = nullptr;while (cur) {parent = cur;if (cur->_data < data) {cur = cur->_pRight;}else if (cur->_data > data) {cur = cur->_pLeft;}else {return false;}}cur = new Node(data);cur->_pParent = parent;if (parent->_data > data) {parent->_pLeft = cur;}else {parent->_pRight = cur;}while (parent) {if (cur == parent->_pLeft) {parent->_bf--;}else {parent->_bf++;}if (parent->_bf == 0) break;if (abs(parent->_bf) == 1) {cur = parent;parent = parent->_pParent;continue;}else if (abs(parent->_bf) == 2) {if (parent->_bf == 2 && cur->_bf == 1) {RotateL(parent);}else if(parent->_bf == 2 && cur->_bf == -1) {RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1) {RotateLR(parent);}else {RotateR(parent);}break;}else {assert(false);}}while (parent != nullptr && parent->_pParent != nullptr) {parent = parent->_pParent;}_pRoot = parent;return true;
}