网站建设签约全网营销国际系统
目录
快速排序
第k个数
归并排序
逆序对的数量
二分查找
数的范围
浮点数二分
高精度
高精度加法
高精度减法
高精度乘法(高精度x低精度)
高精度除法
前缀和与差分
前缀和
子矩阵的和
差分
差分矩阵
快速排序

思路:
- 确认分界点:x=q[(l+r)/2]
- 调整范围,使得在x左边的数小于x,右边的数大于x
- 递归处理左右两端
#include <iostream>using namespace std;const int N = 1000010;int q[N];void quick_sort(int q[],int l,int r)
{if(l>=r) return ;int i=l-1,j=r+1,x=q[l+r>>1];while(i<j){do i++; while(q[i]<x); //碰到大于x的停止do j--; while(q[j]>x); //碰到小于x的停止if(i<j) swap(q[i],q[j]);} //最终使得在x左边的数小于x,右边的数大于xquick_sort(q,l,j); //对左区间进行处理quick_sort(q,j+1,r);
}int main()
{int n;scanf("%d", &n);for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);quick_sort(q, 0, n - 1);for (int i = 0; i < n; i ++ ) printf("%d ", q[i]);return 0;
}
第k个数

#include<iostream>
using namespace std;
int n,a[1000001],k;void qsort(int a[],int l,int r)
{if(l>=r) return ;int i=l-1,j=r+1,x=a[l+r>>1];while(i<j){do i++; while(a[i]<x);do j--; while(a[j]>x);if(i<j) swap(a[i],a[j]);}qsort(a,l,j);qsort(a,j+1,r);
}
int main()
{cin>>n>>k;for(int i=0;i<n;i++) cin>>a[i];qsort(a,0,n-1);cout<<a[k-1]<<" ";
}归并排序

思路:
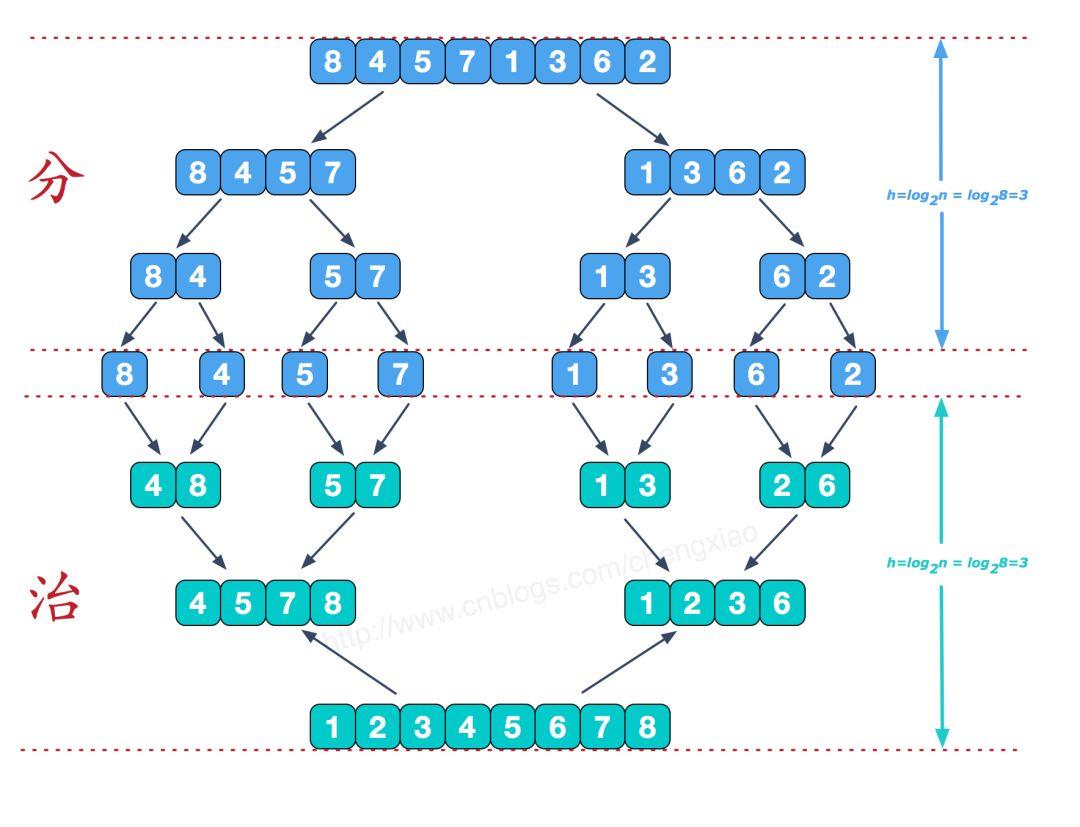
- 递归均分如图区间
- 对每层区间数值按照从小到大顺序存入tmp(可能是奇数无法均分,需要将剩余直接着存入)
- 将该层tmp中排好序的数值放入原来的q中
- 回溯到上一层,重复2,3操作,直到最顶层的left>=right,排序完成
#include<iostream>
using namespace std;
const int N = 1000010;
int n;
int q[N], tmp[N];void merge_sort(int q[], int l, int r)
{if (l >= r) return;int mid = l + r >> 1;merge_sort(q, l, mid), merge_sort(q, mid + 1, r);//递归均分区间int k = 0, i = l, j = mid + 1;while (i <= mid && j <= r)if (q[i] <= q[j]) tmp[k++] = q[i++];//按照从小到大顺序存入tmpelse tmp[k++] = q[j++];while (i <= mid) tmp[k++] = q[i++]; //将剩余的接着存入while (j <= r) tmp[k++] = q[j++];for (i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];//把排好的数放回q
}
int main()
{scanf("%d", &n);for (int i = 0; i < n; i++) scanf("%d", &q[i]);merge_sort(q, 0, n - 1);for (int i = 0; i < n; i++) printf("%d ", q[i]);return 0;
}逆序对的数量
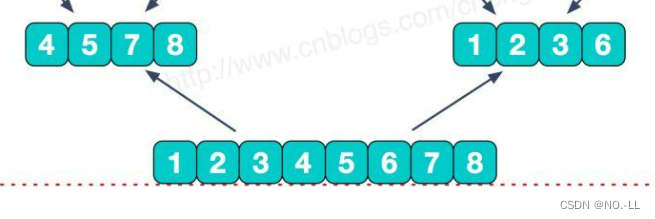
- 归并排序合并过程中计算逆序对数量
- 若 a[i] > a[j],则a[i] 和它后面的元素都大于 a[j],a[i] 构成逆序对数量:res += mid - i + 1;
例如上图合并的一个过程,由4 5 7 8 1 2 3 6 合并为 1 2 3 4 5 6 7 8,对于4有 4>1 所以逆序对数res 就等于4后面的所有数字再加自己本身,即res==(mid-i) +1;
观察整个合并图发现,对每个小的数组合并成大数组累加逆序对,最终不重不漏得到所有逆序对
#include <iostream>using namespace std;typedef long long LL;const int N = 1e5 + 10;int a[N], tmp[N];LL merge_sort(int q[],int l,int r)
{if(l>=r) return 0;int mid =l+r >>1;LL res=merge_sort(q,l,mid)+merge_sort(q,mid+1,r);int k=0,i=l,j=mid+1;//设每个数组的头元素位置while(i<=mid && j<=r){if(q[i]<=q[j]) tmp[k++]=q[i++];else{res+=mid-i+1;tmp[k++]=q[j++];}}while(i<=mid) tmp[k++]=q[i++];while(j<=r) tmp[k++]=q[j++];for(i=l,j=0;i<=r;i++,j++) q[i]=tmp[j];return res;
}int main()
{int n;scanf("%d", &n);for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);cout << merge_sort(a, 0, n - 1) << endl;return 0;
}二分查找
二分模板
//区间[l,r]被划分成[l,mid]和[mid + 1,r]时使用:
int bsearch_1(int 1, int r)
{while (l < r) {int mid = l + r >> 1;if (check(mid)) r = mid; //判断mid是否满足性质else l = mid + 1;}return l;
}//区间[l,r]被划分成[l,mid - 1]和[mid, r]时使用:
int bsearch_2(int l, int r)
{while (l < r) {int mid = l + r + 1 >> 1;if (check(mid)) l = mid; else r = mid - 1;}return l;
}记忆口诀:有减必有加
数的范围

思路:
- 利用二分,保证每次缩小范围时所求值都在范围中
- 一个需要找到>=x的第一个数,另一个需要找到<=x的最后一个数
#include <algorithm>
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int q[N];int SL(int l, int r, int x) {while (l < r) {int mid = l + r >> 1;if (q[mid] >= x) r = mid;else l = mid + 1 ;}return l;//最终找到>=x的第一个数
}int SR (int l, int r, int x) {while (l < r) {int mid = l + r + 1 >> 1;if(q[mid] <= x) l = mid;else r = mid - 1;}return r;//最终找到<=x的第一个数
}int main() { int n,m;scanf ("%d%d",&n,&m);for(int i=0;i<n;++i) scanf ("%d",&q[i]);while ( m-- ) {int x;scanf ("%d",&x);int l = SL(0, n - 1, x);//查找左边界 并返回下标lif (q[l]!=x) cout <<"-1 -1"<<endl;//如果找不到 返回-1 -1else {cout << l << ' '; //如果找到了 输出左下标cout << SR(0, n - 1, x) << endl; //输出右下标}}return 0;
}浮点数二分

思路:
因为完全不必考虑 m=(l+r)/2;导致精度丢失的问题,所以可以直接缩范围

(借用大佬笔记)
#include<iostream>
using namespace std;
int main()
{double l=-100000,r=100000; //数据结果必在其之间,不用思考double n,m;cin>>n;while(r-l>1e-8) //精确到为1e-6,所以至少要多精确两位{m=(l+r)/2;if(m*m*m>=n) r=m; //立方根n在mid的左边,缩右边界else l=m;}printf("%.6f",m);return 0;
}高精度
高精度加法

思路:

#include <iostream>
using namespace std;const int N = 100010;
int A[N], B[N], C[N];int Add(int a[], int b[], int c[], int cnt) {int t = 0;//t表示进位for (int i=1; i<=cnt; i++) {t += a[i] + b[i];//进位加上a和b第i位上的数c[i] = t % 10;//c的值就是进位的个位数t /= 10;//把t的个位数去掉只剩下十位数,即只剩下这个位置的进位}if (t) c[++cnt] = 1;//如果t==1,表示还有一个进位,要补上return cnt;
}int main() {string a, b;cin >> a >> b; //A和B倒着放进int数组,因为有进位,倒着放容易处理int cnt1 = 0;for (int i=a.size()-1; i>=0; i--)A[++cnt1] = a[i] - '0';int cnt2 = 0;for (int i=b.size()-1; i>=0; i--)B[++cnt2] = b[i] - '0';int tot = Add(A, B, C, max(cnt1, cnt2));//因为A和B是倒着放的,所以C也要倒着输出for (int i=tot; i>=1; i--)cout << C[i];
}高精度减法

模拟手算减法
#include<iostream>
#include<vector>
#include<algorithm>
#include<string>
using namespace std;string a,b;
bool cmp(vector<int>&A,vector<int>&B)
{if(A.size()!=B.size()) return A.size()>B.size();for(int i=A.size()-1;i>=0;i--)if(A[i]!=B[i]) return A[i]>B[i];return true; //A==B
}vector<int> sub(vector<int>&A,vector<int>&B)
{vector<int> C;for(int i=0,t=0;i<A.size();i++){t=A[i]-t; //借位if(i<B.size()) t-=B[i]; //两数相减C.push_back((t+10)%10); //如果t>0,入t;如果t<0,入(t+10)%10if(t<0) t=1;else t=0;}while(C.size()>1 && C.back()==0) C.pop_back();return C;
}int main()
{vector<int> A,B;cin>>a>>b;for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');vector<int> C;if(cmp(A,B)) C=sub(A,B);else C=sub(B,A),cout<<"-";for(int i=C.size()-1;i>=0;i--) cout<<C[i];cout<<endl;return 0;
}高精度乘法(高精度x低精度)

#include<iostream>
#include<vector>
using namespace std;vector<int> mul(vector<int>& A,int b)
{vector<int> C;int t=0;for(int i=0;i<A.size();i++){t+=A[i]*b;C.push_back(t%10);t/=10;}while(t){C.push_back(t%10);t/=10;}while(C.size()>1&&C.back()==0) C.pop_back();//去除前导0return C;
}int main()
{string a;int b;cin>>a>>b;vector<int> A;for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');vector<int> C=mul(A,b);for(int i=C.size()-1;i>=0;i--) cout<<C[i];return 0;
}高精度除法

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;vector<int> div(vector<int>&A,int B,int &r)
{vector<int> C;for(int i=0;i<A.size();i++)//模拟手算除法{r=r*10+A[i];C.push_back(r/B);r%=B;}reverse(C.begin(),C.end());//去除前导0while(C.size()>1&&C.back()==0)C.pop_back();return C;
}int main()
{string a;int B,r=0;cin>>a>>B;vector<int> A;for(int i=0;i<a.size();i++)A.push_back(a[i]-'0');vector<int> C=div(A,B,r);for(int i=C.size()-1;i>=0;i--) cout<<C[i];//返回为反转的,反转输出调正cout<<endl<<r;return 0;
}前缀和与差分
前缀和

思路:
给出ai的值时算出前n项和的值
只需要 s[r]-s[l-1] 即可求出 l 到 r 之间的值
技巧:
ios::sync_with_stdio(false);作用:提高cin和cout的速度
副作用:不能使用scanf和printf
#include<iostream>
using namespace std;
const int N=1e6+10;int n,m;
int a[N],s[N];int main()
{ios::sync_with_stdio(false);cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];s[i]=s[i-1]+a[i];}while(m--){int l,r;cin>>l>>r;cout<<s[r]-s[l-1]<<endl;}return 0;
}子矩阵的和

思路:
s[i][j]为从(1,1)到(i,j)所有整数的和
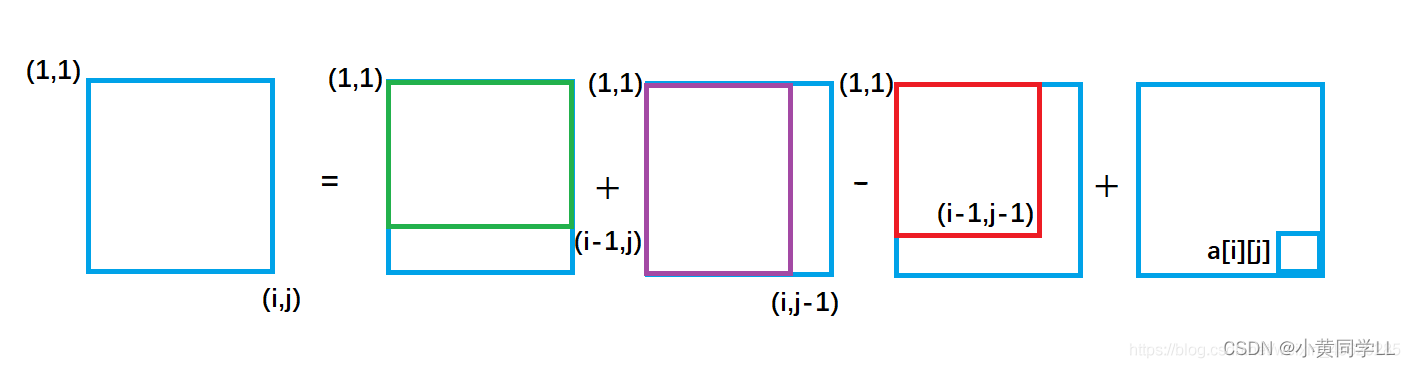
S[i,j]即为所有数的的和为:S[i,j]=S[i,j−1]+S[i−1,j]−S[i−1,j−1]+a[i,j]
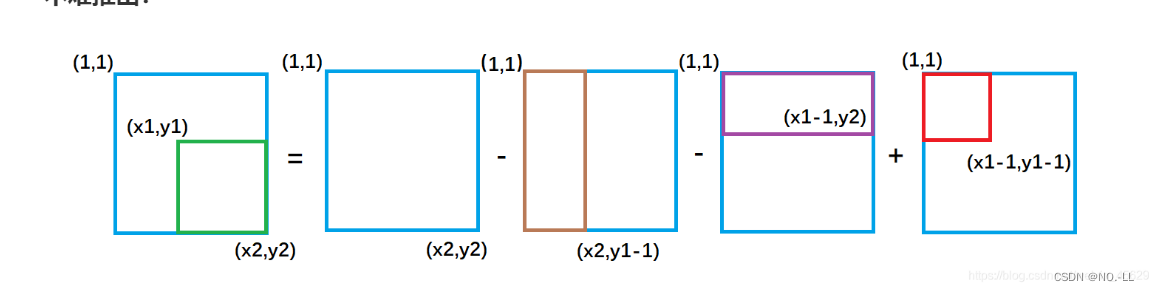
(x1,y1),(x2,y2)这一子矩阵中的所有数之和为:S[x2,y2]−S[x1−1,y2]−S[x2,y1−1]+S[x1−1,y1−1]
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 1010;int n, m, q;
int a[N][N], s[N][N];int main()
{cin>>n>>m>>q;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){cin>>a[i][j];s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];}while(q--){int x1,x2,y1,y2;cin>>x1>>y1>>x2>>y2;cout<<s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]<<endl;}return 0;
}差分

思路:
首先给定一个原数组a:a[1], a[2], a[3],,,,,, a[n];
然后我们构造一个数组b : b[1] ,b[2] , b[3],,,,,, b[i];
使得 a[i] = b[1] + b[2 ]+ b[3] +,,,,,, + b[i]
a数组是b数组的前缀和数组,比如对b数组的b[i]的修改,会影响到a数组中从a[i]及往后的每一个数。
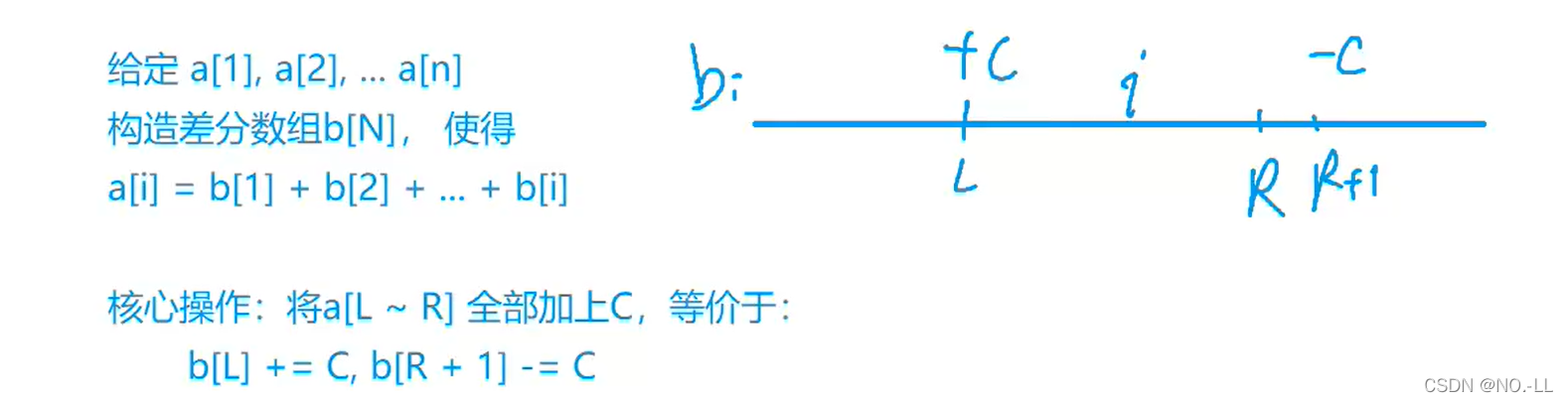
首先让差分b数组中的 b[l] + c ,a数组变成 a[l] + c ,a[l+1] + c,,,,,, a[n] + c;
然后我们打个补丁,b[r+1] - c, a数组变成 a[r+1] - c,a[r+2] - c,,,,,,,a[n] - c;
核心操作:对差分数组b做 b[l] + = c, b[r+1] - = c(时间复杂度为O(1) )
a[i]为b[i]前缀和的实现
令a[i]=a[i-1]+b[i]; ---> b[i]=a[i]-a[i-1];
即:
a[0 ]= 0;
b[1] = a[1] - a[0];
b[2] = a[2] - a[1];
b[3] =a [3] - a[2];
........
b[n] = a[n] - a[n-1];
总结a[i]为b[i]的前缀和 a[i] = b[1] + b[2 ]+ b[3] +,,,,,, + b[i]
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N];
int main()
{int n, m;scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++){scanf("%d", &a[i]);b[i] = a[i] - a[i - 1]; //由前缀和公式,构建差分数组}int l, r, c;while (m--){scanf("%d%d%d", &l, &r, &c);b[l] += c; //将序列中[l, r]之间的每个数都加上cb[r + 1] -= c;}for (int i = 1; i <= n; i++){a[i] = b[i] + a[i - 1]; //更新a[i],前缀和运算printf("%d ", a[i]);}return 0;
}差分矩阵

思路:
a[][]数组是b[][]数组的前缀和数组(b[i][j]改变影响a[i][j]之后的所以值),那么b[][]是a[][]的差分数组,我们去构造差分数组: b[i][j],使得a数组中a[i][j]是b数组左上角(1,1)到右下角(i,j)所包围矩形元素的和
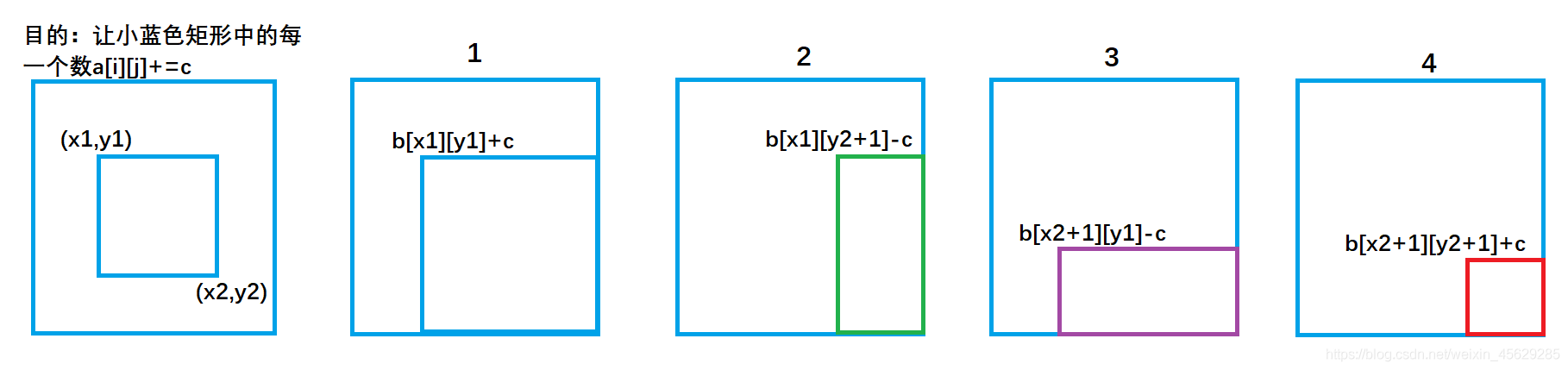
先看核心操作:在范围(x1,y1)到(x2,y2)的方形数组中加c
b[x1][y1] + = c;
b[x1,][y2+1] - = c;
b[x2+1][y1] - = c;
b[x2+1][y2+1] + = c;
(假设有b差分数组)
完成上述操作需要构造差分数组b:
void insert(int x1,int y1,int x2,int y2,int c){ //对b数组执行插入操作,等价于对a数组中的(x1,y1)到(x2,y2)之间的元素都加上了cb[x1][y1]+=c;b[x2+1][y1]-=c;b[x1][y2+1]-=c;b[x2+1][y2+1]+=c;}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){insert(i,j,i,j,a[i][j]); //构建差分数组}}差分这样构建的原因:首先假设a,b都为空数组,也就是全部为0的情况,那么我们也可以说,b数组是a数组的差分数组!因为a[i][j] = b[1][1]+…b[i][j],因为都是0,所有情况满足!在这时a数组其实不为空,我们把a数组中的值看作(0+a[i][j])那么a数组的值变了,变成了a[i][j],这时如果b数组要想成为a数组的差分数组,值也要变为a[i][j],所以我们把b[i][j]变为a[i][j],这样就能满足b数组是a数组的差分数组。也就相当于想b数组中插入a[i][j].
#include<iostream>
#include<cstdio>
using namespace std;
const int N = 1e3 + 10;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
{b[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c;
}
int main()
{int n, m, q;cin >> n >> m >> q;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)cin >> a[i][j];for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){insert(i, j, i, j, a[i][j]); //构建差分数组}}while (q--){int x1, y1, x2, y2, c;cin >> x1 >> y1 >> x2 >> y2 >> c;insert(x1, y1, x2, y2, c);}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]; //二维前缀和//从(1,1)到(i,j)的整数和b[i][j] = b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]+b[i][j]}}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){printf("%d ", b[i][j]);}printf("\n");}return 0;
}