购物网站配色怎么设计一个网站可以优化多少关键词

1 为什么需要四叉树？

路径规划的本质是在给定环境中寻找从起点到终点的最优或可行路径，其核心挑战在于如何高效处理环境信息。传统栅格法将环境均匀划分为等大小的网格，虽直观但面临“维度灾难”——环境规模扩大时，计算量呈指数级增长。例如，一个100×100的二维栅格地图需维护10000个节点，而三维环境下这一数字将飙升至百万级别。拓扑图路径规划算法的核心思想在于将复杂的高维连续空间抽象为低维的离散图结构。基于障碍边界的可视图法(运动规划实战案例 | 基于可视图的路径规划算法(附ROS C++/Python仿真))以及维诺图法(路径规划 | 详解维诺图Voronoi算法(附ROS C++/Python/Matlab仿真))都属于这类基于拓扑图的路径规划。

本文介绍的四叉树(Quadtree)这一数据结构，源于计算机图形学中对二维空间的层次化分割思想：通过递归地将空间划分为四个象限（即“四叉”），仅在需要时对特定区域进行细化，从而实现对空间信息的自适应管理。例如，在开阔区域使用粗粒度划分以节省内存，在障碍物密集区域则进行多级细分以提升路径精度。这种按需分配的特性，使得四叉树在面对非均匀分布的环境时，能够显著降低数据存储与处理的冗余度

接下来，将详细介绍基于四叉树路径规划的算法原理

2 基于四叉树的路径规划

基于四叉树的路径规划(Quartree-based Path Planning)分为三个核心模块：分层抽象、路图搜索与动态剪枝

2.1 分层抽象

四叉树的构建始于将整个环境空间视为一个根节点，随后递归执行分割-判断过程：若当前节点对应的区域完全自由或完全被障碍物占据，则停止分割；若区域同时包含自由空间与障碍物，则将其均等分为四个子节点。这一过程持续至达到预设分割深度或满足精度要求，最终形成一棵层次化的树结构。例如，在机器人导航场景中，四叉树会在走廊等简单区域保持顶层粗划分，而在办公室桌椅排列的复杂区域自动生成多层细粒度节点。这种分层抽象的特性，为路径规划算法提供了天然的优化通道，因为四叉树可通过节点状态快速排除无效区域：若某个父节点被标记为完全障碍，其所有子节点无需进一步探查；若父节点完全自由，则可直接将其作为整体加入开放列表。这种“剪枝”机制大幅减少了状态扩展次数。

2.2 路图搜索

首先，四叉树路图利用已有的树节点作为路图顶点。具体而言，选择满足以下条件的四叉树节点作为路图节点：

• 叶子节点中的自由节点，保证路径可达性
• 非叶子节点中的自由父节点，用于跨层路径跳跃

两个四叉树节点被判定为相邻需满足几何边界接触条件：

• 水平相邻节点需满足纵向坐标范围存在重叠且横向边界间距在容差内(下图红框)
• 垂直相邻节点需满足横向坐标范围存在重叠且纵向边界间距在容差内(下图蓝框)

每个四叉树节点的中心点作为路径搜索的潜在航路点，相邻节点间建立带权无向边，边的权重通常取两节点中心点的欧氏距离。最终形成的路图本质上是一个由自由空间节点及其连接关系构成的图结构，其中节点密度在障碍物边界区域显著增加，确保路径能够精确绕行复杂障碍。

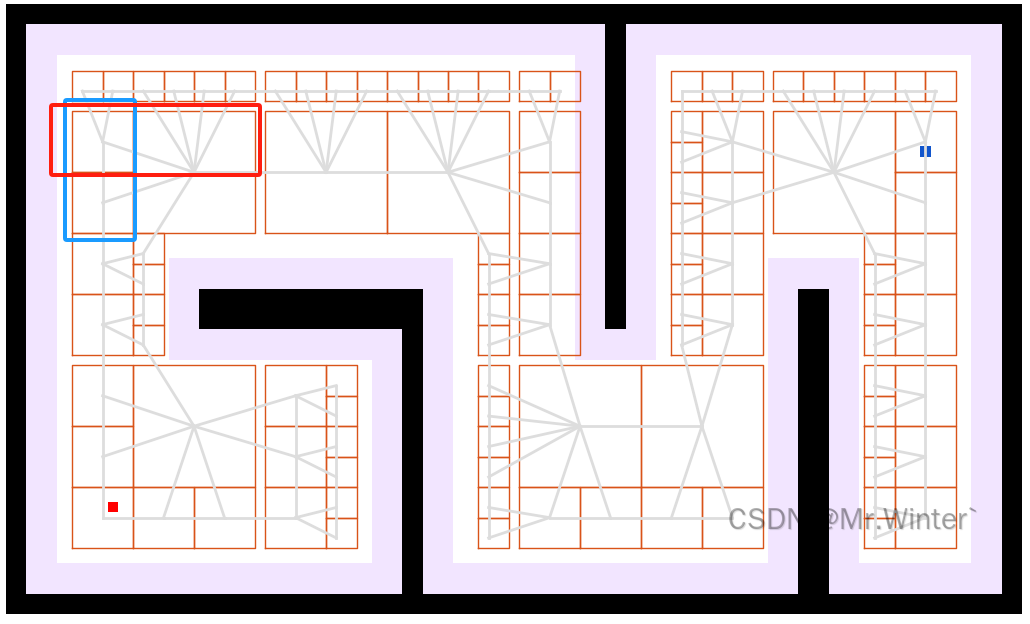
路径搜索过程依托构建完成的路图展开，采用Dijkstra算法即可。

2.3 动态剪枝

当环境中出现临时障碍物（如突然出现的行人或车辆）时，传统方法往往需要全局重新规划，而四叉树只需更新受影响区域的局部节点。具体而言，系统仅需回溯至包含障碍物变化的父节点层级，重新评估其子节点状态，并选择性触发局部重构。这种增量式更新策略使得路径规划系统能够以非常低的代价响应环境变化

3 算法仿真

3.1 ROS C++算法仿真

核心代码如下所示

bool QuartreePathPlanner::plan(const Point3d& start, const Point3d& goal, Points3d& path, Points3d& expand)
{double m_start_x, m_start_y, m_goal_x, m_goal_y;if ((!validityCheck(start.x(), start.y(), m_start_x, m_start_y)) ||(!validityCheck(goal.x(), goal.y(), m_goal_x, m_goal_y))){return false;}// construct quartree only onceif (!is_quartree_valid_){const size_t grids_num = quar_grids_.size();roadmap_.resize(grids_num);valid_edges_.reserve(grids_num * 4);for (size_t i = 0; i < grids_num; ++i){const auto& current = quar_grids_[i];for (size_t j = i + 1; j < grids_num; ++j){const auto& neighbor = quar_grids_[j];if ((std::abs(current.min_x() - neighbor.max_x()) <= 1.0 ||std::abs(current.max_x() - neighbor.min_x()) <= 1.0)){if (current.min_y() < neighbor.max_y() && current.max_y() > neighbor.min_y()){valid_edges_.emplace_back(current.center(), neighbor.center());const double dist = (current.center() - neighbor.center()).length();roadmap_[i].emplace_back(j, dist);roadmap_[j].emplace_back(i, dist);}}else if ((std::abs(current.min_y() - neighbor.max_y()) <= 1.0 ||std::abs(current.max_y() - neighbor.min_y()) <= 1.0)){if (current.min_x() < neighbor.max_x() && current.max_x() > neighbor.min_x()){valid_edges_.emplace_back(current.center(), neighbor.center());const double dist = (current.center() - neighbor.center()).length();roadmap_[i].emplace_back(j, dist);roadmap_[j].emplace_back(i, dist);}}}}is_quartree_valid_ = true;}...// search on quartree mapstd::vector<int> q_path;if (_searchOnRoadMap(roadmap_, start_idx, goal_idx, q_path)){path.clear();path.emplace_back(start);if (q_path.size() > 2){for (size_t i = 1; i < q_path.size() - 1; ++i){const auto& pt = vertices_[q_path[i]];// convert to world framedouble wx, wy;costmap_->mapToWorld(pt.x(), pt.y(), wx, wy);path.emplace_back(wx, wy);}}path.emplace_back(goal);return true;}else{return false;}
}

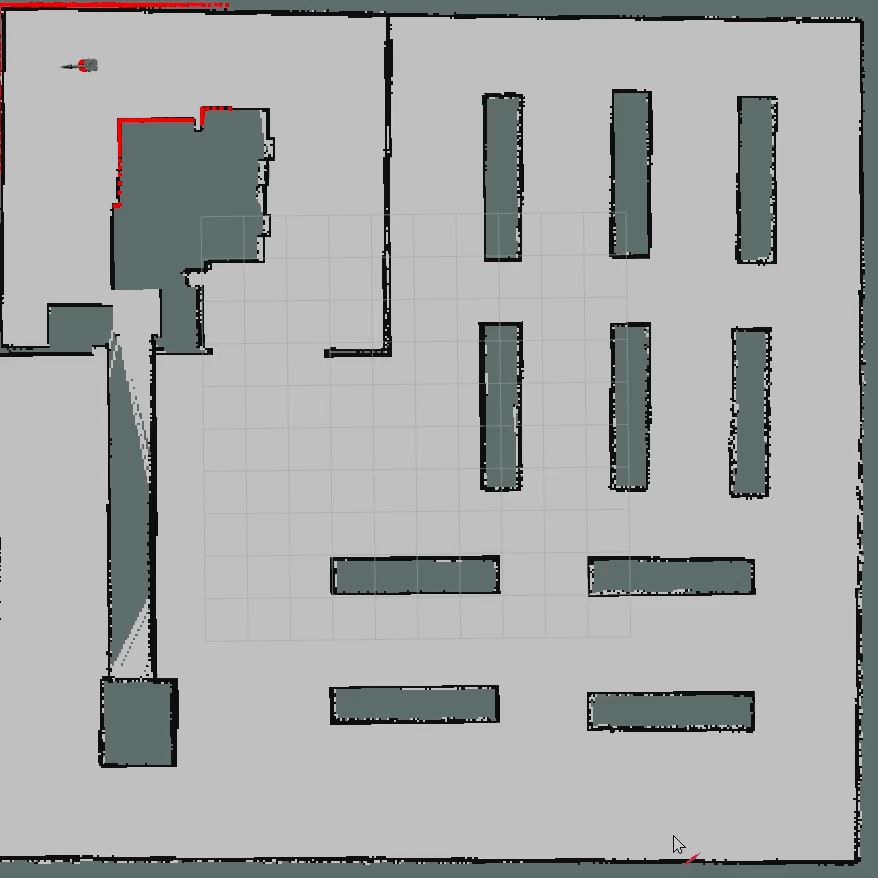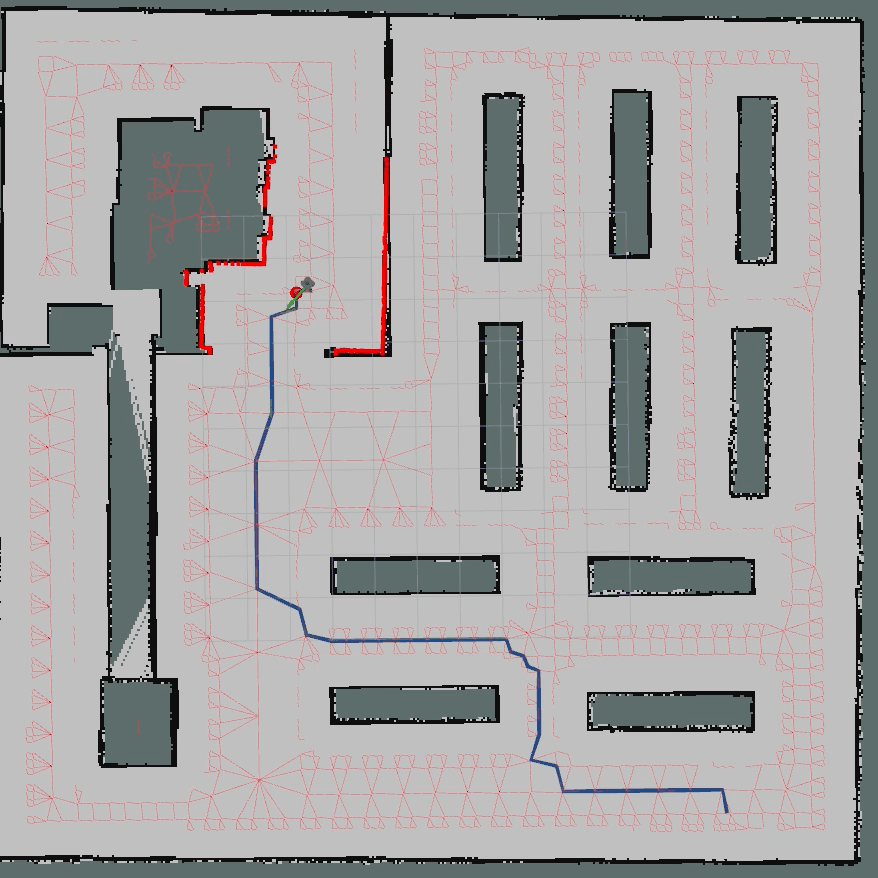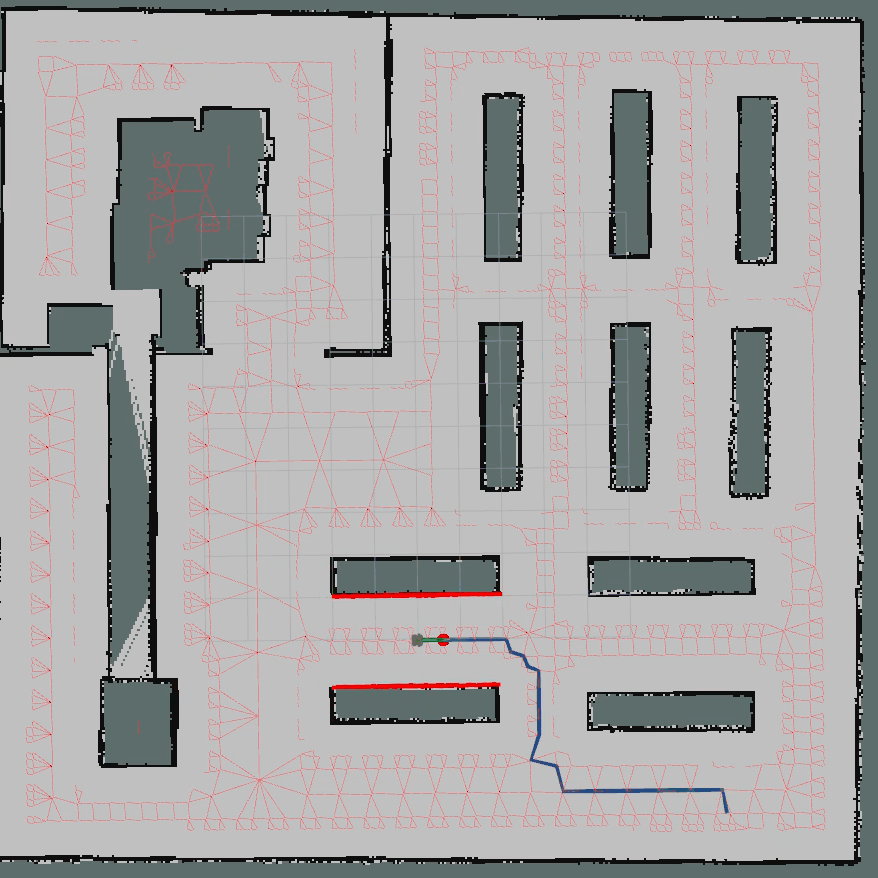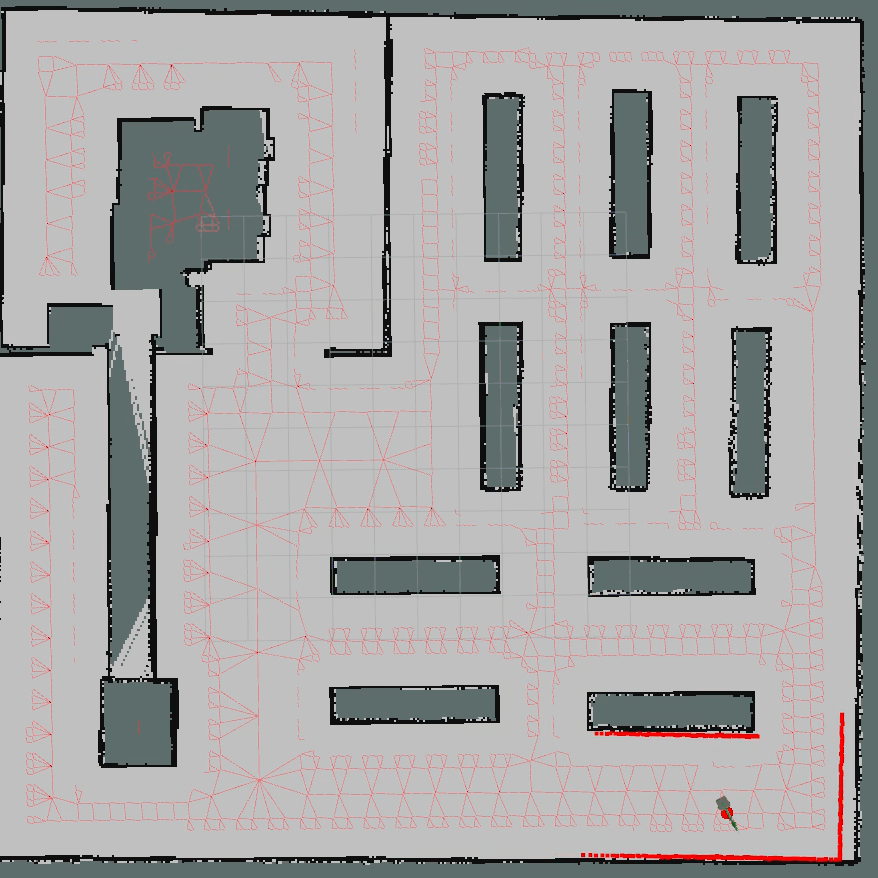
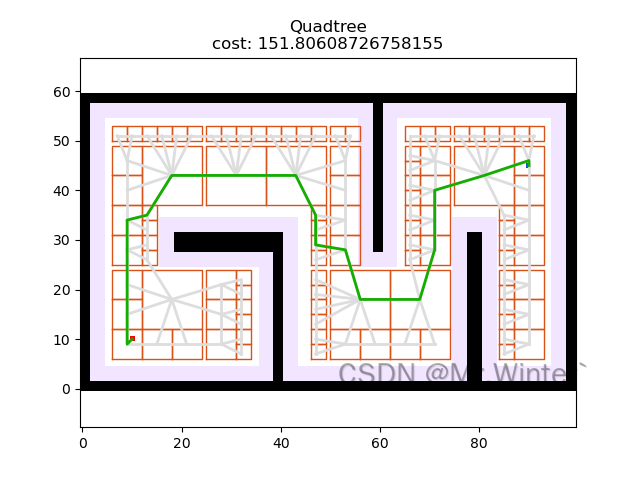
3.2 Python算法仿真

核心代码如下所示

def partition(self, grid: np.ndarray, x: int, y: int, size: int, square_size_threshold: int = 5) -> List[Square]:"""Recursively divides the grid into four parts. If a part contains obstacles it further divied into four more parts.Parameters:grid (np.ndarray): 2D array representing the grid.x, y (int): Top-left coordinates of the current partition.size (int): Size of the current partition.Returns:List of Square objects representing free spaces in the grid."""if size < square_size_threshold:bottom_left = Point3d(x, y)top_right = Point3d(x + size, y + size)if self.isFree(grid, bottom_left, top_right):return [Square(bottom_left, top_right)]else:return []else:# Check if the area is homogeneous and free spaceif self.isFree(grid, Point3d(x, y), Point3d(x + size, y + size)):return [Square(Point3d(x, y), Point3d(x + size, y + size))]else:# Divide the area into quadrants and partition recursivelynew_size = size // 2quad1 = self.partition(grid, x, y, new_size)quad2 = self.partition(grid, x, y + new_size, new_size)quad3 = self.partition(grid, x + new_size, y, new_size)quad4 = self.partition(grid, x + new_size, y + new_size, new_size)return quad1 + quad2 + quad3 + quad4

完整工程代码请联系下方博主名片获取

---

🔥 更多精彩专栏：

• 《ROS从入门到精通》
• 《Pytorch深度学习实战》
• 《机器学习强基计划》
• 《运动规划实战精讲》
• …

👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇