网站做专题页面商品推广软文范例100字
继续聚类算法的学习
@浙大疏锦行
DBSCAN聚类
Q1. 该算法的原理是什么?


总体而言,DBSCAN聚类是一种基于密度的聚类算法,适合发现任意形状的簇和检测噪声点
Q2. 代码实现
import numpy as np
import pandas as pd
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
import matplotlib.pyplot as plt
import seaborn as sns# 评估不同 eps 和 min_samples 下的指标
# eps这个参数表示邻域的半径,min_samples表示一个点被认为是核心点所需的最小样本数。eps_range = np.arange(0.3, 0.8, 0.1) # 测试 eps 从 0.3 到 0.7,步长为0.1
min_samples_range = range(3, 8) # 测试 min_samples 从 3 到 7
results = [] # 用于保存每组参数下的评估结果for eps in eps_range: # 遍历每一个eps取值for min_samples in min_samples_range: # 遍历每一个min_samples取值dbscan = DBSCAN(eps=eps, min_samples=min_samples) # 创建DBSCAN对象dbscan_labels = dbscan.fit_predict(X_scaled) # 对标准化后的数据聚类,得到标签# 计算簇的数量(排除噪声点 -1)n_clusters = len(np.unique(dbscan_labels)) - (1 if -1 in dbscan_labels else 0)# 计算噪声点数量n_noise = list(dbscan_labels).count(-1)# 只有当簇数量大于 1 且有有效簇时才计算评估指标if n_clusters > 1:# 排除噪声点后计算评估指标mask = dbscan_labels != -1if mask.sum() > 0: # 确保有非噪声点silhouette = silhouette_score(X_scaled[mask], dbscan_labels[mask]) # 轮廓系数ch = calinski_harabasz_score(X_scaled[mask], dbscan_labels[mask]) # CH指数db = davies_bouldin_score(X_scaled[mask], dbscan_labels[mask]) # DB指数results.append({'eps': eps,'min_samples': min_samples,'n_clusters': n_clusters,'n_noise': n_noise,'silhouette': silhouette,'ch_score': ch,'db_score': db })
print(f"eps={eps:.1f}, min_samples={min_samples}, 簇数: {n_clusters}, 噪声点: {n_noise}, "
f"轮廓系数: {silhouette:.3f}, CH 指数: {ch:.2f}, DB 指数: {db:.3f}")else:
print(f"eps={eps:.1f}, min_samples={min_samples}, 簇数: {n_clusters}, 噪声点: {n_noise}, 无法计算评估指标")# 将结果转为 DataFrame 以便可视化和选择参数
results_df = pd.DataFrame(results)打印结果

代码继续(绘制评估指标图)
plt.figure(figsize=(15, 10))
# 轮廓系数图
plt.subplot(2, 2, 1)
for min_samples in min_samples_range:subset = results_df[results_df['min_samples'] == min_samples] # plt.plot(subset['eps'], subset['silhouette'], marker='o', label=f'min_samples={min_samples}')
plt.title('轮廓系数确定最优参数(越大越好)')
plt.xlabel('eps')
plt.ylabel('轮廓系数')
plt.legend()
plt.grid(True)# CH 指数图
plt.subplot(2, 2, 2)
for min_samples in min_samples_range:subset = results_df[results_df['min_samples'] == min_samples]plt.plot(subset['eps'], subset['ch_score'], marker='o', label=f'min_samples={min_samples}')
plt.title('Calinski-Harabasz 指数确定最优参数(越大越好)')
plt.xlabel('eps')
plt.ylabel('CH 指数')
plt.legend()
plt.grid(True)# DB 指数图
plt.subplot(2, 2, 3)
for min_samples in min_samples_range:subset = results_df[results_df['min_samples'] == min_samples]plt.plot(subset['eps'], subset['db_score'], marker='o', label=f'min_samples={min_samples}')
plt.title('Davies-Bouldin 指数确定最优参数(越小越好)')
plt.xlabel('eps')
plt.ylabel('DB 指数')
plt.legend()
plt.grid(True)# 簇数量图
plt.subplot(2, 2, 4)
for min_samples in min_samples_range:subset = results_df[results_df['min_samples'] == min_samples]plt.plot(subset['eps'], subset['n_clusters'], marker='o', label=f'min_samples={min_samples}')
plt.title('簇数量变化')
plt.xlabel('eps')
plt.ylabel('簇数量')
plt.legend()
plt.grid(True)plt.tight_layout()
plt.show()

代码继续(进行聚类)
# 选择 eps 和 min_samples 值(根据图表选择最佳参数)
selected_eps = 0.6 # 根据图表调整
selected_min_samples = 6 # 根据图表调整# 使用选择的参数进行 DBSCAN 聚类
dbscan = DBSCAN(eps=selected_eps, min_samples=selected_min_samples)
dbscan_labels = dbscan.fit_predict(X_scaled)
X['DBSCAN_Cluster'] = dbscan_labels# 使用 PCA 降维到 2D 进行可视化
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)# DBSCAN 聚类结果可视化
plt.figure(figsize=(6, 5))
sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], hue=dbscan_labels, palette='viridis')
plt.title(f'DBSCAN Clustering with eps={selected_eps}, min_samples={selected_min_samples} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()# 打印 DBSCAN 聚类标签的分布
print(f"DBSCAN Cluster labels (eps={selected_eps}, min_samples={selected_min_samples}) added to X:")
print(X[['DBSCAN_Cluster']].value_counts())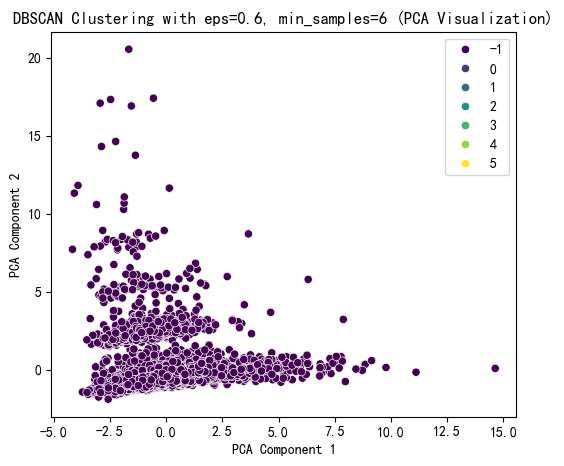
DBSCAN Cluster labels (eps=0.6, min_samples=6) added to X:
DBSCAN_Cluster
-1 74520 122 93 84 71 65 6
dtype: int64从聚类的结果来看,这次聚类失败,因为没有少数簇的数目太少。
对此,提出问题:
Q3. 如何判断DBSCAN聚类是否成功?(除了聚类评估指标外)


层次聚类
Q1. 什么是?
Agglomerative Clustering 是一种自底向上的层次聚类方法,初始时每个样本是一个簇,然后逐步合并最相似的簇,直到达到指定的簇数量或满足停止条件。由于它需要指定簇数量(类似于 KMeans),我们将通过测试不同的簇数量 n_clusters 来评估聚类效果,并使用轮廓系数(Silhouette Score)、CH 指数(Calinski-Harabasz Index)和 DB 指数(Davies-Bouldin Index)。
Q2. 代码实现
import numpy as np
import pandas as pd
from sklearn.cluster import AgglomerativeClustering
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
import matplotlib.pyplot as plt
import seaborn as sns# 标准化数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 评估不同 n_clusters 下的指标
n_clusters_range = range(2, 11) # 测试簇数量从 2 到 10
silhouette_scores = []
ch_scores = []
db_scores = []for n_clusters in n_clusters_range:agglo = AgglomerativeClustering(n_clusters=n_clusters, linkage='ward') # 使用 Ward 准则合并簇agglo_labels = agglo.fit_predict(X_scaled)# 计算评估指标silhouette = silhouette_score(X_scaled, agglo_labels)ch = calinski_harabasz_score(X_scaled, agglo_labels)db = davies_bouldin_score(X_scaled, agglo_labels)silhouette_scores.append(silhouette)ch_scores.append(ch)db_scores.append(db)print(f"n_clusters={n_clusters}, 轮廓系数: {silhouette:.3f}, CH 指数: {ch:.2f}, DB 指数: {db:.3f}")# 绘制评估指标图
plt.figure(figsize=(15, 5))# 轮廓系数图
plt.subplot(1, 3, 1)
plt.plot(n_clusters_range, silhouette_scores, marker='o')
plt.title('轮廓系数确定最优簇数(越大越好)')
plt.xlabel('簇数量 (n_clusters)')
plt.ylabel('轮廓系数')
plt.grid(True)# CH 指数图
plt.subplot(1, 3, 2)
plt.plot(n_clusters_range, ch_scores, marker='o')
plt.title('Calinski-Harabasz 指数确定最优簇数(越大越好)')
plt.xlabel('簇数量 (n_clusters)')
plt.ylabel('CH 指数')
plt.grid(True)# DB 指数图
plt.subplot(1, 3, 3)
plt.plot(n_clusters_range, db_scores, marker='o')
plt.title('Davies-Bouldin 指数确定最优簇数(越小越好)')
plt.xlabel('簇数量 (n_clusters)')
plt.ylabel('DB 指数')
plt.grid(True)plt.tight_layout()
plt.show()Q. 什么是“Ward准则”?

打印结果
n_clusters=2, 轮廓系数: 0.336, CH 指数: 685.66, DB 指数: 2.659
n_clusters=3, 轮廓系数: 0.242, CH 指数: 659.40, DB 指数: 2.327
n_clusters=4, 轮廓系数: 0.254, CH 指数: 565.74, DB 指数: 2.160
n_clusters=5, 轮廓系数: 0.276, CH 指数: 519.91, DB 指数: 2.110
n_clusters=6, 轮廓系数: 0.284, CH 指数: 494.24, DB 指数: 1.860
n_clusters=7, 轮廓系数: 0.295, CH 指数: 482.64, DB 指数: 1.680
n_clusters=8, 轮廓系数: 0.297, CH 指数: 479.17, DB 指数: 1.435
n_clusters=9, 轮廓系数: 0.301, CH 指数: 481.85, DB 指数: 1.283
n_clusters=10, 轮廓系数: 0.309, CH 指数: 489.27, DB 指数: 1.269
代码继续(进行聚类)
# 提示用户选择 n_clusters 值(这里可以根据图表选择最佳簇数)
selected_n_clusters = 10 # 示例值,根据图表调整# 使用选择的簇数进行 Agglomerative Clustering 聚类
agglo = AgglomerativeClustering(n_clusters=selected_n_clusters, linkage='ward')
agglo_labels = agglo.fit_predict(X_scaled)
X['Agglo_Cluster'] = agglo_labels# 使用 PCA 降维到 2D 进行可视化
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)# Agglomerative Clustering 聚类结果可视化
plt.figure(figsize=(6, 5))
sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], hue=agglo_labels, palette='viridis')
plt.title(f'Agglomerative Clustering with n_clusters={selected_n_clusters} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()# 打印 Agglomerative Clustering 聚类标签的分布
print(f"Agglomerative Cluster labels (n_clusters={selected_n_clusters}) added to X:")
print(X[['Agglo_Cluster']].value_counts())
Agglomerative Cluster labels (n_clusters=10) added to X:
Agglo_Cluster
4 5230
1 778
2 771
9 409
5 127
6 96
0 37
3 34
7 10
8 8
dtype: int64代码继续(绘制树状图)
# 层次聚类的树状图可视化
from scipy.cluster import hierarchy
import matplotlib.pyplot as plt# 假设 X_scaled 是标准化后的数据
# 计算层次聚类的链接矩阵
Z = hierarchy.linkage(X_scaled, method='ward') # 'ward' 是常用的合并准则# 绘制树状图
plt.figure(figsize=(10, 6))
hierarchy.dendrogram(Z, truncate_mode='level', p=3) # p 控制显示的层次深度
# hierarchy.dendrogram(Z, truncate_mode='level') # 不用p这个参数,可以显示全部的深度
plt.title('Dendrogram for Agglomerative Clustering')
plt.xlabel('Cluster Size')
plt.ylabel('Distance')
plt.show()

注:
1. 横坐标代表每个簇对应样本的数据,这些样本数目加一起是整个数据集的样本数目。这是从上到下进行截断,p=3显示最后3层,不用p这个参数会显示全部。
2. 纵轴代表距离 ,反映了在聚类过程中,不同样本或簇合并时的距离度量值。距离越大,意味着两个样本或簇之间的差异越大;距离越小,则差异越小。
今日学习到这里,明日继续加油!!!
