当前位置：首页 > wzjs >正文

免费信息网站建设平台西安网站制作

wzjs 2025/8/19 14:27:25

免费信息网站建设平台,西安网站制作,晋城网站建设,免费建站的方法前言AVL树是最早被发明的自平衡二叉查找树，由G. M. Adelson-Velsky和E. M. Landis在1962年的论文中提出。本文将详细介绍AVL树的原理，并通过C代码实现一个完整的AVL树结构。一、AVL树的基本概念AVL树是一种高度平衡的二叉搜索树，它通过平衡因…

前言

AVL树是最早被发明的自平衡二叉查找树，由G. M. Adelson-Velsky和E. M. Landis在1962年的论文中提出。本文将详细介绍AVL树的原理，并通过C++代码实现一个完整的AVL树结构。

一、AVL树的基本概念

AVL树是一种高度平衡的二叉搜索树，它通过平衡因子（Balance Factor）来维护树的平衡性。对于AVL树中的任意节点，其左右子树的高度差（平衡因子）绝对值不超过1。

平衡因子的定义

平衡因子 = 右子树高度 - 左子树高度

在AVL树中，每个节点的平衡因子只能是-1、0或1。当插入或删除节点导致平衡因子的绝对值超过1时，就需要通过旋转操作来恢复平衡。

二、AVL树节点的定义

template<class K, class V>
struct AVLTreeNode {pair<K, V> _kv;                 // 键值对AVLTreeNode<K, V>* _left;       // 左子节点AVLTreeNode<K, V>* _right;      // 右子节点AVLTreeNode<K, V>* _parent;     // 父节点int _bf;                        // 平衡因子AVLTreeNode(const pair<K, V>& kv): _kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0) {}
};

三、AVL树的插入操作

AVL树的插入操作分为两个主要步骤：

按照二叉搜索树的规则插入新节点
更新平衡因子并检查是否需要旋转

bool Insert(const pair<K, V>& kv) {// 树为空时直接插入if (_root == nullptr) {_root = new Node(kv);return true;}// 查找插入位置Node* parent = nullptr;Node* cur = _root;while (cur) {if (cur->_kv.first < kv.first) {parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first) {parent = cur;cur = cur->_left;}else {return false;  // 键已存在}}// 创建新节点并插入cur = new Node(kv);if (parent->_kv.first < kv.first) {parent->_right = cur;}else {parent->_left = cur;}cur->_parent = parent;// 更新平衡因子while (parent) {if (cur == parent->_left) {parent->_bf--;}else {parent->_bf++;}// 根据平衡因子决定下一步操作if (parent->_bf == 0) {break;  // 树已平衡}else if (parent->_bf == 1 || parent->_bf == -1) {// 继续向上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2) {// 需要旋转if (parent->_bf == 2 && cur->_bf == 1) {RotateL(parent);  // 左旋}else if (parent->_bf == -2 && cur->_bf == -1) {RotateR(parent);  // 右旋}else if (parent->_bf == 2 && cur->_bf == -1) {RotateRL(parent); // 右左旋}else if (parent->_bf == -2 && cur->_bf == 1) {RotateLR(parent); // 左右旋}break;}else {assert(false);  // 平衡因子异常}}return true;
}

四、AVL树的旋转操作

AVL树通过四种旋转操作来保持平衡：

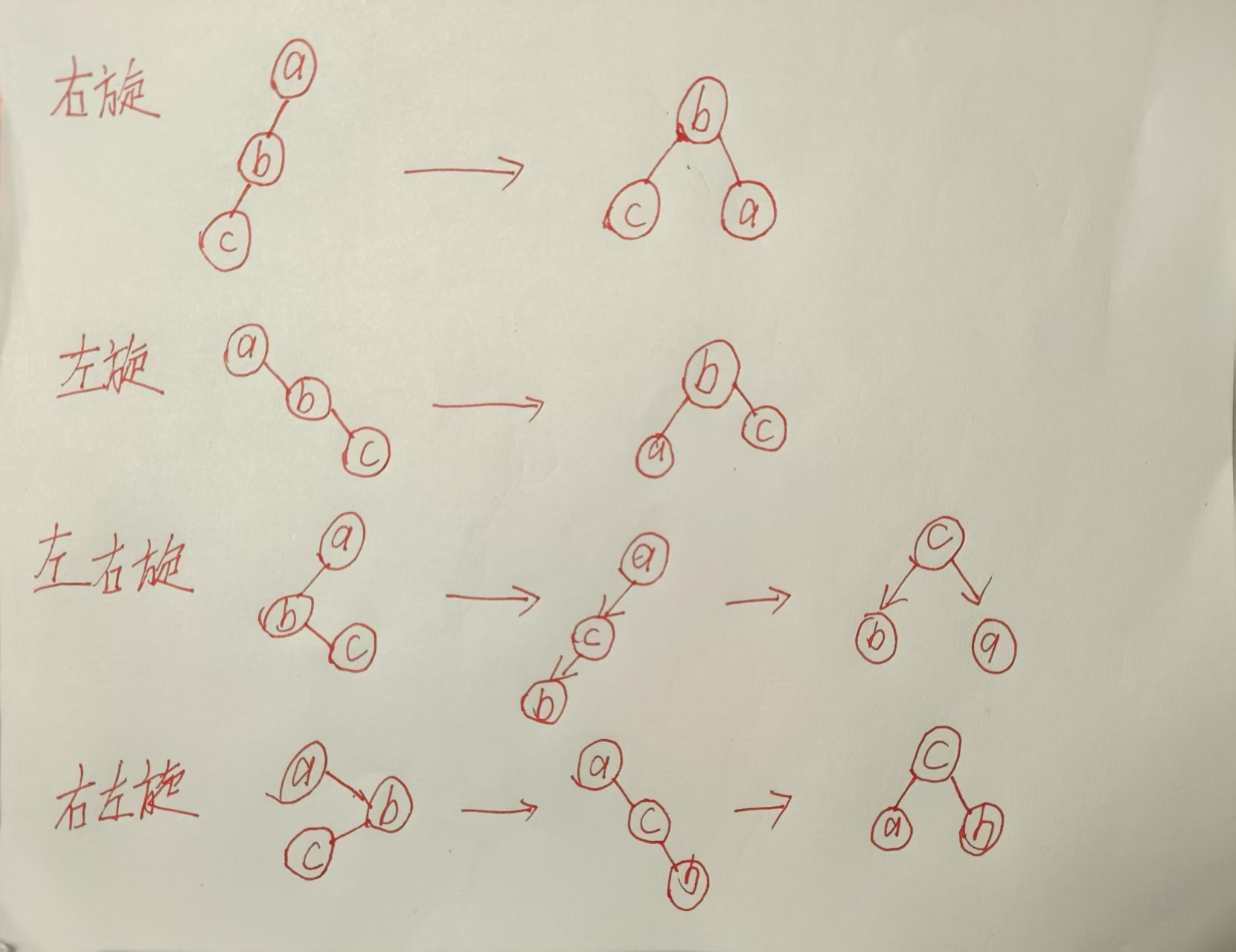
1. 左旋

void RotateL(Node* parent) {Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;if (curleft) {curleft->_parent = parent;}cur->_left = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root) {_root = cur;cur->_parent = nullptr;}else {if (ppnode->_left == parent) {ppnode->_left = cur;}else {ppnode->_right = cur;}cur->_parent = ppnode;}cur->_bf = parent->_bf = 0;
}

2. 右旋（RR型不平衡）

void RotateR(Node* parent) {Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;if (curright) {curright->_parent = parent;}cur->_right = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root) {_root = cur;cur->_parent = nullptr;}else {if (ppnode->_right == parent) {ppnode->_right = cur;}else {ppnode->_left = cur;}cur->_parent = ppnode;}cur->_bf = parent->_bf = 0;
}

3. 左右旋

void RotateLR(Node* parent) {Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;RotateL(parent->_left);RotateR(parent);// 更新平衡因子if (bf == 0) {parent->_bf = 0;curright->_bf = 0;cur->_bf = 0;}else if (bf == -1) {parent->_bf = 1;cur->_bf = 0;curright->_bf = 0;}else if (bf == 1) {parent->_bf = 0;cur->_bf = -1;curright->_bf = 0;}else {assert(false);}
}

4. 右左旋

void RotateRL(Node* parent) {Node* cur = parent->_right;Node* curleft = cur->_left;int bf = cur->_left->_bf;RotateR(parent->_right);RotateL(parent);// 更新平衡因子if (bf == 0) {cur->_bf = 0;curleft->_bf = 0;parent->_bf = 0;}else if (bf == 1) {cur->_bf = 0;curleft->_bf = 0;parent->_bf = -1;}else if (bf == -1) {cur->_bf = 1;curleft->_bf = 0;parent->_bf = 0;}else {assert(false);}
}

五、平衡性检查

为了保证我们的AVL树实现正确，我们需要一个方法来检查树的平衡性：

bool IsBalance() {return IsBalance(_root);
}bool IsBalance(Node* root) {if (root == nullptr) {return true;}int leftHight = Height(root->_left);int rightHight = Height(root->_right);if (rightHight - leftHight != root->_bf) {cout << "平衡因子异常：" << root->_kv.first << "->" << root->_bf << endl;return false;}return abs(rightHight - leftHight) < 2 && IsBalance(root->_left) && IsBalance(root->_right);
}int Height(Node* root) {if (root == nullptr)return 0;int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}