宁波h5模板建站福州seo技术培训
1.最长公共前缀和
题目要求找出所有字符串的公共前缀,如果没有公共的前缀就返回空字符串。
解法1:纵向比较
我们以第一个字符串为标准,依次比较所有字符串的每一位,如果都相同,则比较下一个位置,如果不同,那么前一个位置就是最长的公共前缀。
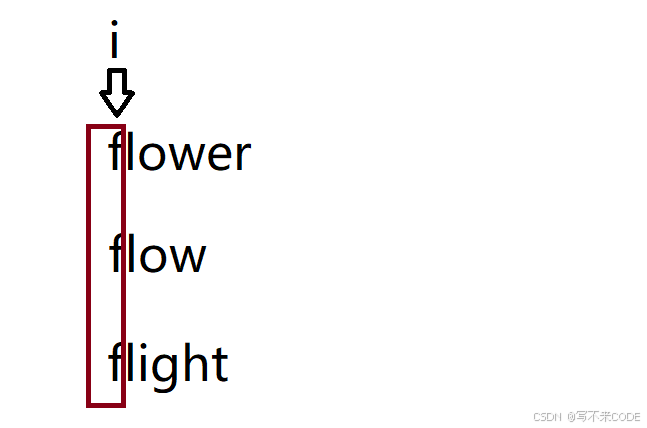
在纵向比较的时候要避免越界,因为第一个字符串的长度有可能比后面的字符串长,所以除了字符不相等外,i越界,也是一个判断条件。
时间复杂度:O(nm),n为数组长度,m为最长的字符串的长度
空间复杂度:O(1)
string longestCommonPrefix(vector<string>& strs) { if(strs.size() == 1) return strs[0];for(int i=0; i<strs[0].size(); ++i){char c = strs[0][i];for(int j=1; j<strs.size(); ++j){if(i == strs[j].size() || strs[j][i] != c)return strs[0].substr(0,i);}}return strs[0];}解法2:横向比较——两两比较
两个两个字符串进行比较,用它们得出的前缀和与第三个字符串继续比较。重复该过程。如果在某一个比较过程中发现前缀和的长度变为0,那就说明所有字符串没有公共的前缀和。
时间复杂度:O(mn),n是数组长度,m是最长的字符串长度
空间复杂度:O(1)
string longestCommonPrefix(vector<string>& strs) { if(strs.size() == 1) return strs[0];string prefix = strs[0];for(int i=0; i<strs.size(); ++i){prefix = compareTwoString(prefix, strs[i]);if(!prefix.size()) break;} return prefix;}string compareTwoString(const string& s1, const string& s2){int index = 0;int minLen = min(s1.size(), s2.size()); //前缀和肯定是在长度较短的字符串中出现while(index < minLen && s1[index] == s2[index]) index++;return s1.substr(0,index);}2.最长回文子串

解法:中心扩展算法
不管是偶数回文串还是奇数回文串,它们都是对称的。所以我们可以固定一个中心元素,然后定义两个指针i,j,分别向两边进行搜索,如果两边元素相等就继续移动,直到不相等或者越界,此时i+1,j-1之间的子串就是最长的回文串。
当然上面求出的是奇数的回文串,所以还需考虑偶数的回文串。我们让i位置不变,j从中心元素位置开始,重复上面的搜索。
不管是奇数还是偶数,每搜索一次就要更新结果,而且我们返回的是子串,所以得直到起始位置和长度。起始位置就是i+1,而长度则是right -1 - (left +1)+1 = right - left - 1.
时间复杂度:O(n^2),枚举每一个中心元素是O(n),向两边搜索合起来也是O(n)
空间复杂度:O(1)
class Solution
{
public:string longestPalindrome(string s) {// 中心扩展算法int begin = 0, length = 0;for(int i=0; i<s.size(); ++i) // 枚举中心元素{// 奇数子串int left = i, right = i;while(left >=0 && right < s.size() && s[left] == s[right]){left--;right ++;}// 更新结果if(right - left - 1 > length){begin = left + 1;length = right - left - 1;}// 偶数子串left = i;right = i + 1;while(left >=0 && right < s.size() && s[left] == s[right]){left--;right ++;}// 更新结果if(right - left - 1 > length){begin = left + 1;length = right - left - 1;}}return s.substr(begin, length);}
};3.二进制求和

这其实就是一道高精度加法,只不过换成了满二进位。模拟竖式加法即可。
时间复杂度:O(max(n,m))
空间复杂度:O(1)
class Solution
{
public:string addBinary(string a, string b) {if(a[0] == '0' || b[0] == '0') return a[0] == '0' ? b : a;string ret;int i = a.size() - 1, j = b.size() - 1;int carry = 0;while(i>=0 || j>=0 || carry) {carry += i>=0?a[i]-'0':0;carry += j>=0?b[j]-'0':0;ret += carry % 2 + '0';carry /= 2;i--;j--;}reverse(ret.begin(), ret.end());return ret;}
};4.字符串相乘 
解法1:模拟——用另一个数的每一位依次和另一个数相乘
用竖式模拟乘法时,其实就是让下面的数的每一位依次和上面的相乘,然后将相乘的结果相加。
所以我们解法一采取的策略就是模拟上述过程。用另一个数的每一位依次和另一个数相乘,但是乘的时候要注意位数,比如1与123相乘时,结果应该时1230,所以我们要对每一次乘积进行补零。接着就是对每一次乘的结果相加,这其实就是一个高精度加法,这个加法我们可以在每一次乘的结果就加上,没必要等到最后在处理。
时间复杂度:O(mn(n+m))
空间复杂度:O(m+n)
class Solution
{
public:string _solve(string s, int multiplier, string multiple)// 被乘数,乘数,倍数{string ret;int carry = 0;for (int i = s.size() - 1; i >= 0 || carry; --i){int x = i >= 0 ? s[i] - '0' : 0;carry += x * multiplier;ret += to_string(carry % 10);carry /= 10;}reverse(ret.begin(), ret.end());return ret + multiple; // 补零操作}// 高精度加法string addTwoString(string s, string t){if (!s.size() || !t.size())return !s.size() ? t : s;int i = s.size() - 1, j = t.size() - 1, carry = 0;string ret;while (i >= 0 || j >= 0 || carry){carry += i < s.size() ? s[i--] - '0' : 0;carry += j < t.size() ? t[j--] - '0' : 0;ret += to_string(carry % 10);carry /= 10;}reverse(ret.begin(), ret.end());return ret;}string multiply(string s, string t) {if (s[0] == '0' || t[0] == '0')return "0";// 依次取出s的每一位 与 t相乘string multiple;int tmp = 0;string ret;for (int i = s.size() - 1; i >= 0; --i){tmp = (s[i] - '0');ret = addTwoString(ret, _solve(t, tmp, multiple));multiple += '0';}return ret;}
};解法2:模拟无进位相乘后相加
做法就是我们直接模拟竖式相乘,但是不管进位,直接存储下来,且对应位置的还应该加在一起,最后统一处理进位,让每个位置只保留一个数。下面模拟一个示例:
根据示例,我们需要存储下对应位置的乘积的和,而且这些乘积的位置是由规律的,逆序相乘,下标从0开始,那么两个数乘积的位置就在i+j处。所以我们创建一个vector用来存储对应位置的乘积的和,最后在对vector里面的数进行进位处理。进位处理时同时要考虑carry!=0的情况。
因为我们是逆序进行操作的,vector里面也是逆序存储的,按照上面的例子来说应该是72 87 21,所以最后还需要进行逆序。但是逆序前还得进行一步——处理前导零。因为我们开的vector空间比较大,但是存储时可能存储不完,就可能导致后面多余了0,我们需要将这些0给删除掉,之后再进行逆置。
class Solution
{
public:string multiply(string nums1, string nums2) {if(nums1[0] == '0' || nums2[0] == '0') return "0";// 无进位相乘int n = nums1.size(), m = nums2.size();vector<int> add_no_carry(n+m); reverse(nums1.begin(), nums1.end());reverse(nums2.begin(), nums2.end());for(int i=0; i<n; ++i){for(int j=0; j<m; ++j){// 对应位置相加add_no_carry[i+j] += (nums1[i] - '0') * (nums2[j] - '0');}}// 处理进位string ret;int carry = 0;for(auto e : add_no_carry){carry += e;ret += carry % 10 + '0';carry /= 10;}while(carry){ret += carry % 10 + '0';carry /= 10;}cout << ret << endl;// 处理前导零,因为还没有将结果逆置回来,多余的0堆积在ret尾部while(ret.size() && ret.back() == '0') ret.pop_back();reverse(ret.begin(), ret.end());return ret;}
};