成都金牛网站建设公司打开浏览器直接进入网站

Mamaba3–RNN、状态方程、勒让德多项式

一、简单回顾

在Mamba1和Mamba2中分别介绍了RNN和状态方程。
下面从两个图和两个公式出发，对RNN和状态方程做简单的回顾：
$RNN:s_t=W{s}_{t-1}+U{x}_t；O_t=V{s}_t$
$状态方程：\widehat{x_t}=A{x}_{t-1}+B{u}_t；y=C{x}_t$


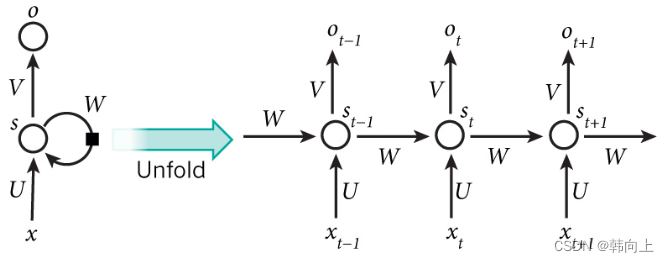
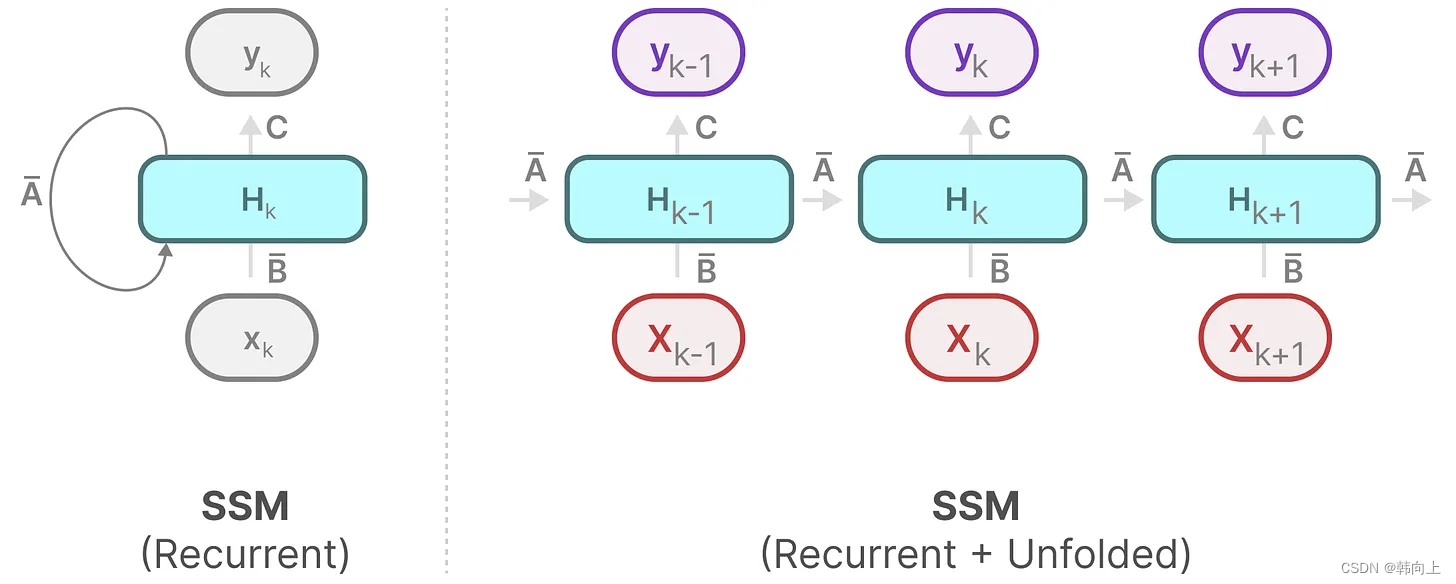
可以看到RNN的本质表达是一个状态方程。
再重复一遍状态变量、状态方程和输出方程的定义，加深理解：
状态变量：刻画系统状态的变量称为状态变量（比如机械系统中的速度、位置）。
状态方程：描述系统输入如何影响状态变量变化的方程。
输出方程：描述状态变量与输出变量关系的一组代数方程。

二、勒让德多项式

勒让德多项式可以被理解为一组多项式基函数，和傅里叶级数类似，允许将某个未知信号分解为不同多项式函数的组合。

三、记忆的本质

记忆是通过重新复盘过去发生的事情，且记忆的内容$\hat{f}(t)$ ≠ 事件本身$f(t)$ 。而是拟合逼近的关系.

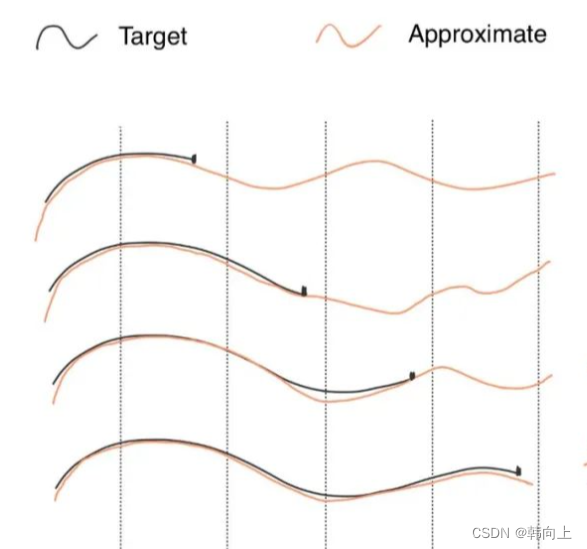
对于一段序列信号，可以被一组基函数(S4中为勒让德多项式)$e_i(t)$进行线性组合来表示。即：
$\hat{f}(t)={\sum }_{i=1}^{\infty }{c}_i{e}_i(t)$

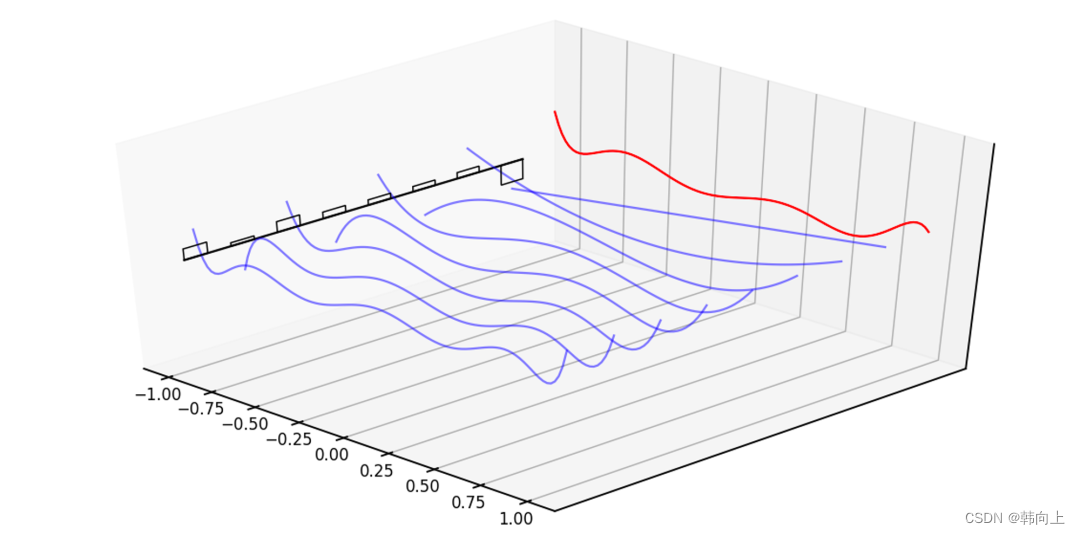
在真实场景中，信号是持续输入的，因此，拟合和逼近也是在持续进行。

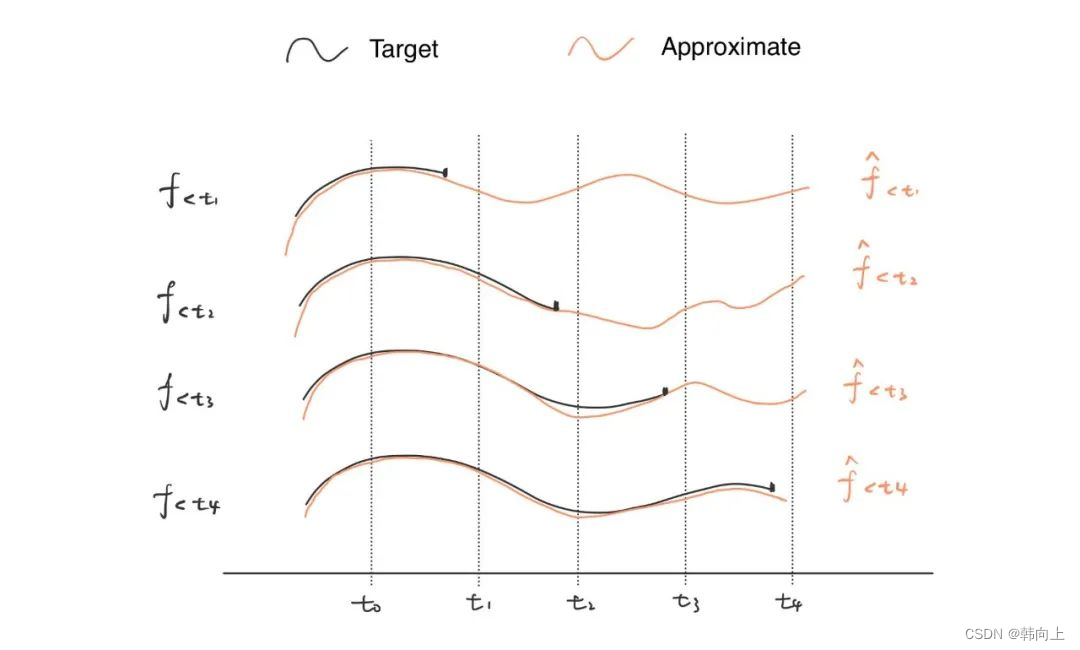
其中$f_{<t}$表示目标函数f在t时刻之前的逼近。即不同时刻对应着不同的拟合系数
$$\begin{gathered} t_1时刻：{\hat{f}}_{<t_1}(t)=\sum _{i=1}^N{c}_{t_1,i}{e}_i(t) \\ {t}_4时刻：{\hat{f}}_{<t_4}(t)=\sum _{i=1}^N{c}_{t_4,i}{e}_i(t) \end{gathered}$$
在上式中，勒让德多项式$e_i(t)$是固定的，$c_i$表示多项式基函数的系数，且随着输入$f(t)$不断更新。 介绍到这里，脑子里有一个想法，前面介绍的状态变量也是随着输入不断的更新！
使用N阶勒让德多项式逼近序列信号，即意味着将信号映射至N维空间中，而$c(t)$是刻画信号的状态变量。

接下来计算$c(t)$。

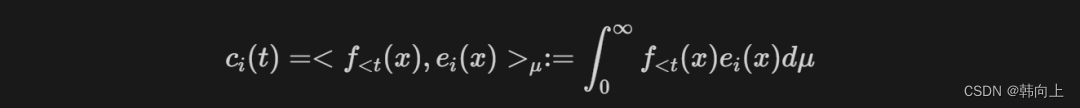
对上面的公式进行微分，并经过数学推理可以得到一个ODE：

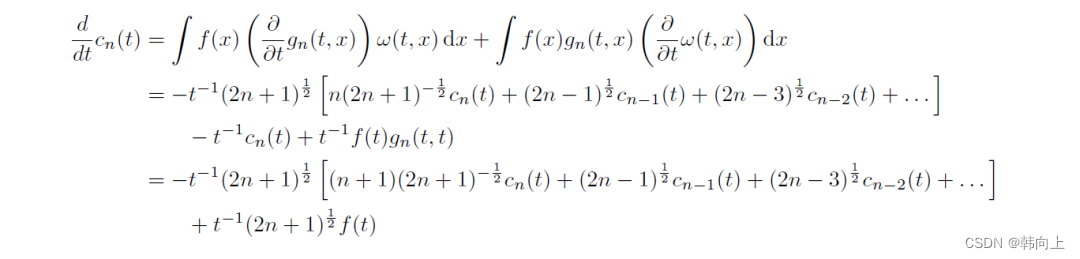
对上式进行整理可得：
$\frac{d}{dt}c(t)=\frac{1}{t}Ac(t)+\frac{1}{t}Bf(t)->\dot{c}(t)=Ac(t)+Bf(t)$
其中，矩阵A（Hippo矩阵）为：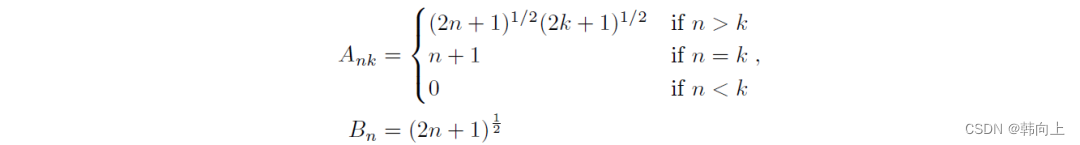

四、总结

本文说明了RNN、SSM与勒让德多项式之间的关系：

• RNN本质上是一个SSM
• S4将序列信号映射至勒让德基函数空间，状态向量即为多项式系数
• S4中将RNN中权重矩阵W替换成Hippo矩阵

额外说明

（PS：Mamba所采用的基本框架仍是S4, Mamba则在S4的基础上引入了若干关键改进，主要可以总结为以下几点：
选择性扫描算法（Selective Scan Algorithm）：Mamba采用了一种硬件感知的并行化算法，称为选择性扫描算法，它能够在加速训练和推理速度的同时，保持对历史上下文的有效利用。与S4相比，Mamba不仅存储整个历史上下文，而且选择性地将部分历史上下文总结为固定上下文，这样既保留了详细的历史信息，又提高了处理效率。
参数化矩阵与Attention效果：Mamba模型通过参数化矩阵对输入信息进行有选择性的处理，类似于注意力机制（Attention），不同输入拥有不同的状态表示，增强了模型对不同token信息的处理能力。
简化的SSM模型：Mamba还可能包含了对SSM（Sparse State Machines或Structured State Machines）的简化，进一步提升了模型的效率和可解释性。）

五、参考文章

[1]一文通透想颠覆Transformer的Mamba：从SSM、HiPPO、S4到Mamba
[2]现代控制理论——状态、状态空间、状态空间描述
[3]Mamba：4 魔幻矩阵A
[4]Mamba：3 记忆殿堂