做网站推广的公司完美日记网络营销策划书
欢迎来到干货小仓库
"普通程序员+Google = 超级程序员"
1、AVL 树的概念
二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。
例如在这种情况下：二叉树的效率退化为(O(N))
通过数学加的研究，对上述情况想到了解决方案：当向二叉搜索树中插入新节点后如果能保证每个节点的左右子树高度之差绝对值不超1(需要对树中的节点进行调整)，即可降低树的高度，从而减少平均搜索长度。
一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：
a、它的左右子树都是AVL树
b、左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
AVL树可以保证其搜索的时间复杂度为
2.AVL树的节点结构定义
template<class T>
struct AVLTreeNode
{AVLTreeNode(const T& data): _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr), _data(data), _bf(0){}AVLTreeNode<T>* _pLeft; // 该节点的左孩子AVLTreeNode<T>* _pRight; // 该节点的右孩子AVLTreeNode<T>* _pParent; // 该节点的双亲T _data;int _bf; // 该节点的平衡因子(控制高度差)
};3.AVL树的插入
AVL树是也是一颗二叉搜索树，只是在二叉搜索树的基础上引入了平衡因子，对每颗子树的高度差不会超过1，从而进行平衡。(高度差：左子树-右子树的绝对值)
AVL 树的插入分为三步
①按照二叉搜索树的放式插入新节点
②调整节点的平衡因子
③对 不符合高度差不超过1 的节点进行旋转
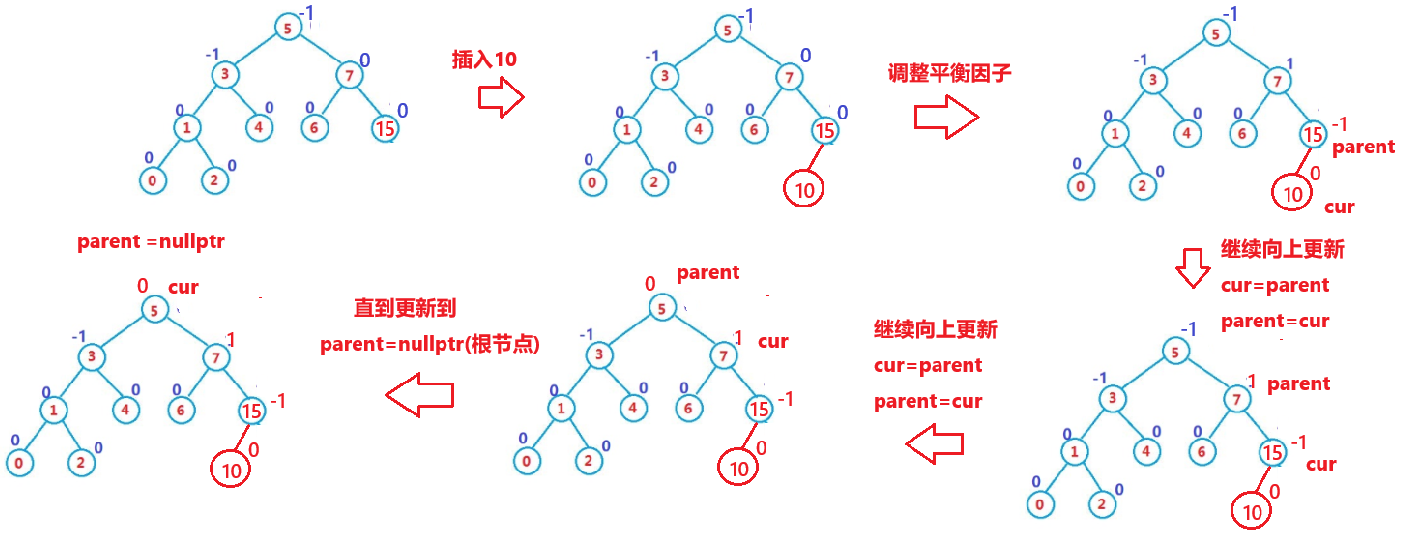
示例：
情况一：一直往上更新
情况二：旋转
3.1更新平衡因子的主要逻辑
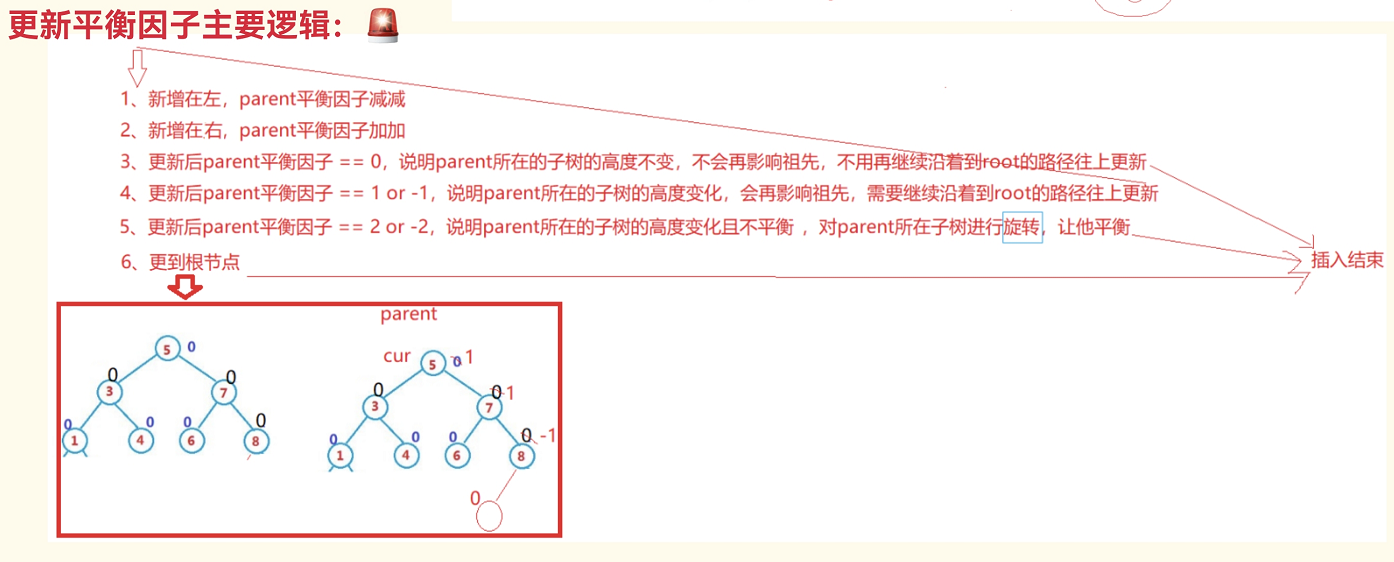
当更新平衡因子时，遇到不满足高度差不超过1时，则进行旋转，降低此树的高度
代码实现：
①找到根据二叉搜索树的插入规则插入相应的节点(此处就不过多展开)
②更新平衡因子
//更新平衡因子while (parent){if (parent->_left == cur)parent->_bf--;elseparent->_bf++;if (parent->_bf == 0)break;else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//根据情况进行旋转//.....return true;}elseassert(false);}
return true;3.2AVL树的旋转规则
①旋转后保持还是搜索树。
②变成平衡树 且 降低这颗子树的高度
3.2.1左单旋
示例：满足(parent的平衡因子为2 && cur的平衡因子为1)条件则进行左单旋
在进行左单旋的时候：其核心操作主要有两步：
parent->right =cur -> left; //将parent的右子树链接到cur的左子树上
cur->left =parent; //cur的左子树指向parent
代码实现：
左单旋
void RotateL(Node* parent)
{Node* cur = parent->_right;Node* curLeft = cur->_left;parent->_right = curLeft;if (curLeft)curLeft->_parent = parent;cur->_left = parent;Node* ppNode = parent->_parent;parent->_parent = cur;//修正cur的父亲if (ppNode == nullptr){cur->_parent = nullptr;_root = cur;}else{if (ppNode->_left == parent)ppNode->_left = cur;elseppNode->_right = cur;cur->_parent = ppNode;}//修改旋转后的平衡因子parent->_bf = cur->_bf = 0;
}3.2.2右单旋
示例：
其核心步骤分为两步：
parent->left =cur -> right; //将parent的右子树链接到cur的右子树上
cur->right =parent; //cur的右子树指向parent
代码实现
void RotateR(Node* parent)
{Node* cur = parent->_left;Node* curRight = cur->_right;parent->_left = curRight;if (curRight)curRight->_parent = parent;cur->_right = parent;Node* ppNode = parent->_parent;parent->_parent = cur;//更新cur的父亲if (ppNode == nullptr){cur->_parent = nullptr;_root = cur;}else{if (ppNode->_left == parent)ppNode->_left = cur;elseppNode->_right = cur;cur->_parent = ppNode;}parent->_bf = cur->_bf = 0;
}3.3.3左右双旋
代码实现
void RotateLR(Node* parent)
{Node* cur = parent->_left;Node* curRight = cur->_right;int bf = curRight->_bf;RotateL(parent->_left);RotateR(parent);// 10// 7// 9if (bf == 0){cur->_bf = 0;curRight->_bf = 0;parent->_bf = 0;}// 13// 7 15// 5 9// 10else if (bf == 1){cur->_bf = -1;curRight->_bf = 0;parent->_bf = 0;}// 13// 7 15// 5 9// 8else if (bf == -1){cur->_bf = 0;curRight->_bf = 0;parent->_bf = 1;}elseassert(false);
}3.3.4右左双旋
满足：parent的平衡因子为2 && cur 的平衡因子为-1 ------>右左双旋
代码实现：
void RotateRL(Node* parent)
{Node* cur = parent->_right;Node* curLeft = cur->_left;int bf = curLeft->_bf;RotateR(parent->_right);RotateL(parent);//修正双旋后的平衡因子if (bf == 0){cur->_bf = 0;curLeft->_bf = 0;parent->_bf = 0;}else if (bf == 1){cur->_bf = 0;curLeft->_bf = 0;parent->_bf = -1;}else if (bf == -1){cur->_bf = 1;curLeft->_bf = 0;parent->_bf = 0;}elseassert(false);
}3.3整体代码实现
bool insert(const pair<K, V>& kv)
{if (_root == nullptr){Node* newNode = new Node(kv);_root = newNode;return true;}//按二叉树搜索树插入逻辑进行插入Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}elsereturn false;}cur = new Node(kv);if (parent->_kv.first > cur->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//更新平衡因子while (parent){if (parent->_left == cur)parent->_bf--;elseparent->_bf++;if (parent->_bf == 0)break;else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//旋转if (parent->_bf == 2 && cur->_bf == 1){//左旋RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent); //右旋}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent); //右左双旋}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent); //左右双旋}elseassert(false);return true;}elseassert(false);}
return true;
}觉得不错的可以点赞+收藏咯！
谢谢大家