做俄语网站建设新的数据新闻
一、说明
描述一个概率模型,有密度函数很好描述。如果写不出密度函数,退而用分布函数也能完整刻画,因此,分布函数表示比密度函数表示更加宽泛普适。本片讲述经验分布拟合分布函数的基础概念。
二、经验分布直观解释
在统计学中,经验分布函数(又称经验累积分布函数,eCDF )是与样本的经验测度相关的分布函数。该累积分布函数是一个阶跃函数,在n 个数据点处,其值在每个数据点上都以1/ n 的幅度跃升。对于任何指定的测量变量值,其值是该测量变量观测值中小于或等于该指定值的比率。

绿色曲线渐近地接近0和1的高度,但未达到这两个高度,它是标准正态分布的真实累积分布函数。
灰色线段表示从该分布中抽取的特定样本的观测值,蓝色阶跃函数的水平阶跃(包括每一步的最左侧点,但不包括最右侧点)构成了该样本的经验分布函数。(单击此处加载新图表。)
经验分布函数是生成样本点的累积分布函数的估计值。根据格利文科-坎泰利定理,它以概率 1 收敛到该基础分布。目前有许多结果可以量化经验分布函数向基础累积分布函数的 收敛速度。
三、经验分布解析表述
设( X 1 , …, X n )为独立同分布的实随机变量,具有共同的累积分布函数 F ( t )。则经验分布函数定义为[

在这里 1 A 1_A 1A是事件A的指标,对于给定的t,指标 1 X i ≤ t {\displaystyle \mathbf {1} _{X_{i}\leq t}} 1Xi≤t是参数为 p = F ( t ) p = F ( t ) p=F(t)的伯努利随机变量;因此
n F ^ n ( t ) {\displaystyle n{\widehat {F}}_{n}(t)} nF n(t)是一个二项式随机变量,均值为 n F ( t ) nF ( t ) nF(t),方差为 n F ( t ) ( 1 − F ( t ) ) nF ( t )(1 − F ( t )) nF(t)(1−F(t))。这意味着 F ^ n ( t ) {\displaystyle {\widehat {F}}_{n}(t)} F n(t)是F ( t )的无偏估计量。
然而,在一些教科书中,其定义如下

四、渐进性质
由于当 n n n趋向无穷大时,比率 ( n + 1 ) / n ( n + 1)/ n (n+1)/n趋近于 1 ,因此上面给出的两个定义的渐近性质是相同的。
根据强大数定律,估计量
F ^ n ( t ) {\displaystyle \scriptstyle {\widehat {F}}_{n}(t)} F n(t)对于t的每一个值,当n → ∞时几乎肯定收敛于F ( t ):

因此估计量 F ^ n ( t ) {\displaystyle \scriptstyle {\widehat {F}}_{n}(t)} F n(t)是一致的。该表达式断言了经验分布函数逐点收敛于真实的累积分布函数。有一个更强的结论,称为格利文科-坎泰利定理,它指出收敛实际上在t上均匀发生:

这个表达式中的 sup-norm 称为Kolmogorov–Smirnov 统计量,用于检验经验分布之间的拟合优度
F ^ n ( t ) {\displaystyle \scriptstyle {\widehat {F}}_{n}(t)} F n(t)以及假设的真实累积分布函数F。这里可以合理地使用其他范数函数来代替 sup 范数。例如,L2范数可以推导出Cramér–von Mises 统计量。
渐近分布可以用几种不同的方式进一步刻画。首先, 中心极限定理指出,逐点 F ^ n ( t ) {\displaystyle \scriptstyle {\widehat {F}}_{n}(t)} F n(t)具有渐近正态分布,标准 n {\displaystyle {\sqrt {n}}} n收敛速度:
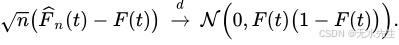
这个结果由Donkser定理扩展。该定理断言经验过程 n ( F ^ n − F ) {\displaystyle \scriptstyle {\sqrt {n}}({\widehat {F}}_{n}-F)} n(F n−F),被视为一个函数,索引为 t ∈ R {\displaystyle \scriptstyle t\in \mathbb {R} } t∈R,在Skorokhod 空间中分布收敛 D [ − ∞ , + ∞ ] {\displaystyle \scriptstyle D[-\infty ,+\infty ]} D[−∞,+∞]均值零高斯过程格 G F = B ∘ F {\displaystyle \scriptstyle G_{F}=B\circ F} GF=B∘F其中B是标准布朗桥。
