怎么做网站动图成都网络运营推广

        前缀和与差分的核⼼思想是预处理，可以在暴⼒枚举的过程中，快速给出查询的结果，从⽽优化时间 复杂度。

        是经典的⽤空间替换时间的做法。

一、⼀维前缀和

题⽬来源：⽜客⽹

题⽬链接：【模板】前缀和

难度系数：★

1. 题目描述 

2. 算法原理

解法一：暴力解法-->模拟（时间复杂度过大，超时）

通过for循环模拟相加，最多 n * q 次

解法二：前缀和-->快速求出数组中模拟区间的和

1. 创建前缀和数组： f [i] = f [i − 1] + a[i]

     2.查询[l, r]区间和：f [r] − f [l − 1]

注意：使用前缀和数组时，建议数组遍历从数组下标位 1 的位置开始，不会出现a[-1]，处理边界情况。

3. 参考代码

#include <iostream>using namespace std;typedef long long LL;const int N = 1e5 + 10;int n, q;
LL a[N];
LL f[N]; // 前缀和数组int main()
{cin >> n >> q;for(int i = 1; i <= n; i++) cin >> a[i];// 处理前缀和数组for(int i = 1; i <= n; i++){f[i] = f[i - 1] + a[i];}// 处理 q 次询问while(q--){int l, r; cin >> l >> r;cout << f[r] - f[l - 1] << endl;}return 0;
}

二、最大子段和

题⽬来源：⽜客⽹

题⽬链接：P1115 最大子段和 - 洛谷

难度系数：★

1. 题目描述 

2. 算法原理

考虑以 i 位置的元素 a[i]「为结尾」的最⼤⼦段和：

• 在求「区间和」时，相当于是⽤ f[i] 减去 i 位置前⾯的某⼀个 f[x]
• 如果想要「最⼤⼦段和」，也就是「最⼤区间和」，那么⽤ f[i] 减掉⼀个「前驱最⼩值」即可。

f[i] 的值是确定的，只要减去前面最小的前驱 prevmin  就能得到最大字段和 ret

        因此，我们可以创建 a 数组的「前缀和」数组，然后在遍历前缀和数组的过程中，⼀边「更新前驱最 ⼩值」，⼀边「更新当前位置为结尾的最⼤⼦段和」。

3. 参考代码

#include <iostream>using namespace std;typedef long long LL;const int N = 2e5 + 10;int n;
LL f[N]; // 前缀和数组int main()
{cin >> n;for(int i = 1; i <= n; i++){LL x; cin >> x;f[i] = f[i - 1] + x;}LL ret = -1e20;LL prevmin = 0;for(int i = 1; i <= n; i++){//当前情况，当前最大值减去前驱最小值 ret = max(ret, f[i] - prevmin);//更新下一个位置的前驱最小值prevmin = min(prevmin, f[i]);}cout << ret << endl;return 0;
}

三、⼆维前缀和

题⽬来源：⽜客⽹

题⽬链接：【模板】二维前缀和

难度系数：★

1. 题目描述

2. 算法原理

解法一：暴力解法-->模拟

使用for循环遍历相加，时间复杂度过大

解法二：二维前缀和-->快速查询二维数组中某一个子矩阵中所有的元素和

        ⼆维前缀和模板题，直接套⽤「公式」创建前缀和矩阵，然后利⽤前缀和矩阵的「性质」处理 次询 问。

1. 创建前缀和矩阵： f [i][j] = f [i − 1][j] + f [i][j − 1] − f [i − 1][j − 1] + a[i][j]

 

1. 查询以(x1 , y1 )为左上⻆ ,(x2 , y2 )为右下⻆的⼦矩阵的和

 

3. 参考代码

#include <iostream>using namespace std;typedef long long LL;const int N = 1010;int n, m, q;
LL f[N][N];int main()
{cin >> n >> m >> q;// 预处理前缀和矩阵for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){LL x; cin >> x;f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + x;}}// 处理 q 次查询while(q--){int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;cout << f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1] << endl;}return 0;
}

四、激光炸弹

题⽬来源：洛⾕

题⽬链接：P2280 [HNOI2003] 激光炸弹 - 洛谷

难度系数：★★

1. 题目描述 

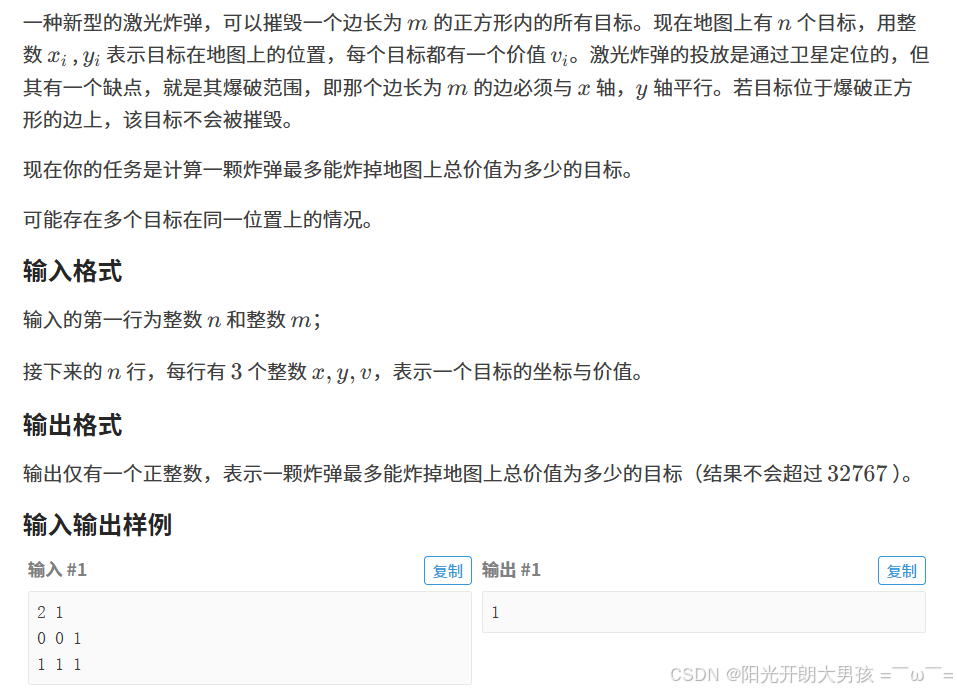
2. 算法原理 

        可以⽤⼀个⼆维矩阵将所有⽬标的价值存起来，其中 a[i][j] 就表⽰ [i, j] 位置的⽬标价值之和。⼀颗炸弹能够获得的价值正好是⼀个 R × R ⼤⼩的⼀个正⽅形内所有⽬标的价值总和，那么我们可以求出  a 可。矩阵的前缀和矩阵，然后枚举所有边⻓为 R 的⼦正⽅形的价值之和，求出⾥⾯的最⼤值即可。

如何枚举边⻓为 R 的所有正⽅形：

• 仅需枚举右下⻆[x2 , y2 ] (R + 1 ≤ x2≤ 5000, R + 1 ≤ y2≤ 5000) ，那么结合边⻓ R 就可算出左上⻆[x2 − R + 1, y2 − R + 1] 。
• 代⼊前缀和矩阵中，就可以快速求出这个正⽅形内所有⽬标的总价值。

细节问题：

• 题⽬中某⼀个位置会「重复」出现，因此 a[i][j]+ = w ；

• 半径 R 可能「超过5000 」 ，此时炸弹可以摧毁所有⽬标，也就是整个矩阵的⽬标价值之和。

3. 参考代码

#include <iostream>
using namespace std;
const int N = 5010;
int n, m;
int a[N][N];
int f[N][N]; // 前缀和矩阵int main()
{cin >> n >> m;while (n--){int x, y, v; cin >> x >> y >> v;x++, y++; // 下标从1开始计数a[x][y] += v; // 同⼀个位置有可能有多个⽬标}n = 5001;// 预处理前缀和矩阵for (int i = 1; i <= n; i++){for (int j = 1; j <= n; j++){f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + a[i][j];}}int ret = 0;m = min(m, n); // 如果m很⼤，相当于就是把整个区域全部摧毁// 枚举所有边⻓为m的正⽅形for (int x2 = m; x2 <= n; x2++){for (int y2 = m; y2 <= n; y2++){int x1 = x2 - m + 1, y1 = y2 - m + 1;ret = max(ret, f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 -1][y1 - 1]);}}cout << ret << endl;return 0;
}