数据结构与算法：算法分析

 遇到的问题，都有解决方案，希望我的博客能为您提供一点帮助。

本篇参考《Data Structures and Algorithm Analysis in C++》 

“在程序设计中，不仅要写出能工作的程序，更要关注程序在大数据集上的运行时间。”

• 本章讨论要点：本篇将探讨：估计程序运行时间、优化运行时间、分析盲目递归后果、讲解求幂和求最大公因数的高效算法。

一、数学基础 

1. 分析原理的数学思想

分析目标：通过比较函数的相对增长率，分析算法的资源消耗（如时间、空间复杂度）。
分析关键点：忽略常数因子和低阶项，关注输入规模 N, N→∞时的主导项。

• ​核心问题：直接比较两个函数在具体点的值（如 f(N)<g(N)）没有意义，因为可能存在交叉点。
• ​关键方法：比较函数的渐近增长率​（即当 N→∞ 时的增长速度），忽略常数因子和低阶项。
• ​转折点（Breakpoint）​：
  例如，1000N 和 N2 的转折点是 N=1000。当 N>1000 时，N2 的增长速度超过 1000N。

2. 渐进符号的定义

(1) 大O符号（O(f(N))）——上界

• ​定义：若存在正常数 c 和 n0​，使得当 N≥n0​ 时，T(N)≤c⋅f(N)，则记 T(N)=O(f(N))。
• ​直观含义：描述函数 T(N) 的增长率不超过 f(N) 的增长率。
• ​例子：
  1000N=O(N2)，因为当 N≥1000 时，1000N≤1⋅N2。
  尽管 1000N 系数较大，但 N2 的增长率更高，最终会超过 1000N。

(2) Ω符号（Ω(g(N))）——下界

• ​定义：若存在正常数 c 和 n0​，使得当 N≥n0​ 时，T(N)≥c⋅g(N)，则记 T(N)=Ω(g(N))。
• ​直观含义：描述函数 T(N) 的增长率不低于g(N) 的增长率。
• ​例子：
  N2=Ω(1000N)，因为当 N≥1，N2≥1000N 总成立（需适当选择 c 和 n0​）。

(3) Θ符号（Θ(h(N))）——紧确界

• ​定义：T(N)=Θ(h(N)) 当且仅当 T(N)=O(h(N)) 且 T(N)=Ω(h(N))。
• ​直观含义：描述函数 T(N) 的增长率与 h(N) 的增长率相等​（即上下界一致）。
• ​例子：    因为其增长率完全由  主导。

(4) o符号（o(p(N))）——严格上界

• ​定义：若对任意正常数 c，存在 n0​，使得当 N≥n0​ 时，T(N)<c⋅p(N)，则记 T(N)=o(p(N))。
• ​直观含义：描述函数 T(N) 的增长率严格小于 p(N) 的增长率。
• ​例子：
  ，因为无论 c 多小（如 c=0.1），当 N 足够大时，。

• Big-O vs 小o:
  Big-O 允许“等于”，如 ；
  小o 严格排除“等于”，如，但 。

3. 作用与用法

(1) 算法效率比较

• 核心用途：通过渐进符号比较不同算法的增长率，判断哪个更高效。

• 用 O 描述算法的最坏时间复杂度​（上界），如快速排序的最坏情况为 。
• 用 Ω 描述算法的最好时间复杂度​（下界），如快速排序的最好情况为 Ω(NlogN)。
• 用 Θ 描述算法的精确时间复杂度，如归并排序的时间复杂度为 Θ(NlogN)。

• 例子：O(Nlog⁡N) 的排序算法（如归并排序）比  的算法（如冒泡排序）更适合大规模数据。

(2) 设计优化方向

• 上界分析（大O）：确保算法在最坏情况下仍可接受。

• 下界分析（Ω）：证明问题的固有复杂度（如排序问题的下界为 Ω(NlogN)）。

• 紧确界（Θ）：精确描述算法的平均性能。

(3) 实际应用技巧

• 忽略常数项：1000N和 0.1N均视为 O(N)。

• 关注最高阶项：对于 ，只需关注。

• 避免误区：大O表示上界，不一定是精确增长率（Θ才是精确描述）。

 小结

• 核心思想：通过渐进符号抽象出算法的增长率，指导工程师选择高效算法。

• ​符号关系：
  O 是上界，Ω 是下界，Θ 是紧确界，o 是严格上界。

• 关键原则：

  • 小规模数据中常数项可能重要，但大规模数据中增长率主导性能。

  • O 用于最坏情况分析，Ω 用于最优情况，Θ 用于平均情况。

  • 严格区分 O 与 o（如 N=o(Nlog⁡N)）。

4. 重要法则与数学工具

​4.1.加法法则

• ​规则：若 T1​(N)=O(f(N))，T2​(N)=O(g(N))，则 T1​(N)+T2​(N)=O(max(f(N),g(N)))。
• ​例子：（保留最高阶项）。

4.2.​乘法法则

• ​规则：若 T1​(N)=O(f(N))，T2​(N)=O(g(N))，则 T1​(N)*T2​(N)=O(f(N)⋅g(N))。
• ​例子：。

4.3.多项式复杂度规则

• 规则：若 T(N)是 k 次多项式，则 。
  例子：。
  作用：快速判断多项式算法的最高阶项。

4.4.​对数增长规则(底为2）

• ​关键结论：对任意常数 k，。
• ​意义：对数函数（如 logN、）的增长率远低于线性函数 N，因此含对数的算法复杂度（如 O(NlogN)）通常优于纯多项式复杂度（如 ）。

5. 相对增长率的判定方法

 

(1) 极限法

通过计算极限  ​ 判断相对增长率：

• 极限为0：f(N)=o(g(N))（如 ）。

• 极限为常数 c≠0：f(N)=Θ(g(N))（如 ）。

• 极限为∞：g(N)=o(f(N))（如 2Nvs N!）。

(2) 洛必达法则

• 适用条件：当 均为 ∞。

• 规则：。
  例子：比较 f(N)=log⁡N和 g(N)=N,，导数为  vs 1，极限为0，故 log⁡N=o(N)。

二、计算模型

1、需要分析的问题主要是运行时间

       影响运行时间因素：程序运行时间受编译器、计算机、算法及输入等因素影响，编译器和计算机超出理论模型范畴，重点讨论算法和输入因素 。运行时间函数定义：定义平均运行时间函数 Tavg​(N) 和最坏情况运行时间函数 Tworst​(N) ，且 Tavg​(N)≤Tworst​(N) ，输入多样时函数可能有多个变量 。不同情形性能分析：最好情形性能分析意义不大，平均情形反映典型行为，最坏情形为性能保障 。强调本书分析算法而非程序，程序实现细节一般不影响大 O 结果，低效实现可能导致程序慢 。选择最坏情况分析原因：默认分析最坏情况运行时间，因其为所有输入提供界限，且平均情况界计算困难，“平均” 定义可能影响分析结果 。

 我们来看看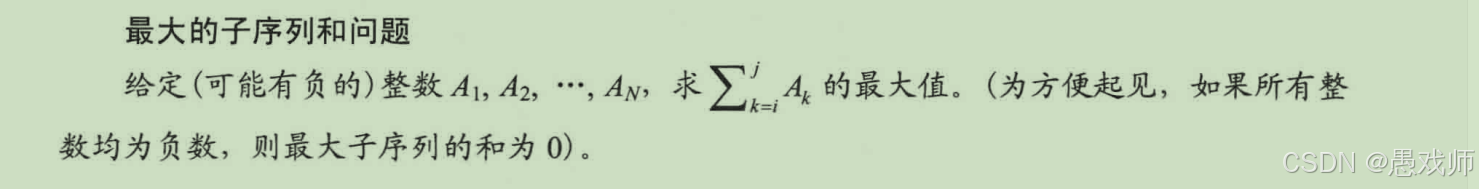

目前不理解没有关系，这个例子的目的是为了展示不同算法运行时间的差异

#include <iostream>
#include <vector>
#include <chrono>
#include <algorithm>
#include <climits>
#include <cstdlib>

using namespace std;
using namespace chrono;

// 1. 暴力解法 O(n³)
int maxSubArrayBruteForceCubic(vector<int>& nums) {
    int max_sum = 0;
    int n = nums.size();
    for (int i = 0; i < n; ++i) {
        for (int j = i; j < n; ++j) {
            int current_sum = 0;
            for (int k = i; k <= j; ++k) {
                current_sum += nums[k];
            }
            max_sum = max(max_sum, current_sum);
        }
    }
    return max_sum;
}

// 2. 优化暴力解法 O(n²)
int maxSubArrayBruteForce(vector<int>& nums) {
    int max_sum = 0;
    int n = nums.size();
    for (int i = 0; i < n; ++i) {
        int current_sum = 0;
        for (int j = i; j < n; ++j) {
            current_sum += nums[j];
            max_sum = max(max_sum, current_sum);
        }
    }
    return max_sum;
}

// 3. 分治法 O(n log n)
int maxCrossingSum(vector<int>& nums, int l, int m, int h) {
    int sum = 0, left_sum = INT_MIN;
    for (int i = m; i >= l; --i) {
        sum += nums[i];
        left_sum = max(left_sum, sum);
    }
    
    sum = 0;
    int right_sum = INT_MIN;
    for (int i = m+1; i <= h; ++i) {
        sum += nums[i];
        right_sum = max(right_sum, sum);
    }
    
    return max({left_sum + right_sum, 0});
}

int maxSubArrayDivideAndConquerHelper(vector<int>& nums, int l, int h) {
    if (l == h) return max(0, nums[l]);
    
    int m = l + (h - l)/2;
    return max({
        maxSubArrayDivideAndConquerHelper(nums, l, m),
        maxSubArrayDivideAndConquerHelper(nums, m+1, h),
        maxCrossingSum(nums, l, m, h)
    });
}

int maxSubArrayDivideAndConquer(vector<int>& nums) {
    if (nums.empty()) return 0;
    return maxSubArrayDivideAndConquerHelper(nums, 0, nums.size()-1);
}

// 4. Kadane算法 O(n)
int maxSubArrayKadane(vector<int>& nums) {
    int max_current = 0, max_global = 0;
    for (int num : nums) {
        max_current = max(num, max_current + num);
        max_global = max(max_global, max_current);
    }
    return max_global;
}

// 生成测试数据
vector<int> generateTestData(int size) {
    vector<int> data;
    srand(time(nullptr));
    for (int i = 0; i < size; ++i) {
        data.push_back(rand() % 200 - 100); // 生成-100到99的随机数
    }
    return data;
}

int main() {
    vector<int> test = generateTestData(100); // 生成100个元素的测试数据
    
    // 运行测试并计时
    auto start = high_resolution_clock::now();
    int result1 = maxSubArrayBruteForceCubic(test);
    auto end = high_resolution_clock::now();
    auto time1 = duration_cast<microseconds>(end - start).count();
    
    start = high_resolution_clock::now();
    int result2 = maxSubArrayBruteForce(test);
    end = high_resolution_clock::now();
    auto time2 = duration_cast<microseconds>(end - start).count();
    
    start = high_resolution_clock::now();
    int result3 = maxSubArrayDivideAndConquer(test);
    end = high_resolution_clock::now();
    auto time3 = duration_cast<microseconds>(end - start).count();
    
    start = high_resolution_clock::now();
    int result4 = maxSubArrayKadane(test);
    end = high_resolution_clock::now();
    auto time4 = duration_cast<microseconds>(end - start).count();

    // 输出结果表格
    cout << "算法\t\t\t时间复杂度\t运行时间(μs)\t结果" << endl;
    cout << "暴力解法\t\tO(n³)\t\t" << time1 << "\t\t" << result1 << endl;
    cout << "优化暴力解法\tO(n²)\t\t" << time2 << "\t\t" << result2 << endl;
    cout << "分治法\t\t\tO(n log n)\t" << time3 << "\t\t" << result3 << endl;
    cout << "Kadane算法\t\tO(n)\t\t" << time4 << "\t\t" << result4 << endl;

    return 0;
}

2、运行时间的计算 

2.1.基本法则

---

2.1.1.法则1：For循环的时间计算

​核心规则

• ​运行时间 = 循环内部语句运行时间 × 迭代次数。
• ​忽略常数项：循环初始化、条件判断等操作的常数时间可忽略（属于低阶项）。

​示例代码

for (i = 0; i < n; ++i) {
    a[i] = 0;  // 单次操作时间为 O(1)
}

• ​分析：
  循环内部语句时间为 O(1)，迭代次数为 n。
  总时间 = O(1)×n=O(n)。

​常见场景

• 遍历数组、链表等线性结构的时间复杂度通常为 O(n)。

---

​2.1.2.法则2：嵌套循环的时间计算

​核心规则

• ​运行时间 = 最内层语句运行时间 × 所有外层循环次数的乘积。
• ​从内向外分析：逐层计算每层循环的迭代次数，最终相乘。

​示例代码

for (i = 0; i < n; ++i) {          // 外层循环：n次
    for (j = 0; j < n; ++j) {      // 内层循环：n次
        a[i] += a[j] + i + j;      // 单次操作时间为 O(1)
    }
}

• ​分析：
  最内层语句时间为 O(1)，总迭代次数为 。
  总时间 = 。

​常见场景

• 双重嵌套循环常见于矩阵操作、暴力搜索等，时间复杂度为 O(n2)。

---

​2.1.3.法则3：顺序语句的时间计算

​核心规则

• ​运行时间 = 各语句运行时间的总和，但最终取最大值（主导项）。
• ​关键原则：仅保留最高阶项，忽略低阶项和常数。

​示例代码

// 第一个循环：O(n)
for (i = 0; i < n; ++i) {
    a[i] = 0;
}

// 第二个循环：O(n^2)
for (i = 0; i < n; ++i) {
    for (j = 0; j < n; ++j) {
        a[i] += a[j] + i + j;
    }
}

• ​分析：
  第一个循环时间为 O(n)，第二个循环时间为 O(n2)。
  总时间 = （取最大值）。

​常见场景

• 若算法包含多个独立步骤，时间复杂度由最耗时的步骤决定。

---

​2.1.4.法则4：If/Else语句的时间计算

​核心规则

• ​运行时间 = 条件判断时间 + max(S1运行时间, S2运行时间)。
• ​保守估计：无论条件是否满足，取两个分支中时间较长者。

​示例代码

if (condition) {        // 条件判断时间为 O(1)
    // S1：O(n^2)
    for (i = 0; i < n; ++i) {
        for (j = 0; j < n; ++j) {
            // ...
        }
    }
} else {
    // S2：O(n)
    for (i = 0; i < n; ++i) {
        // ...
    }
}

• ​分析：
  条件判断时间为 O(1)，S1时间为 O(n^2)，S2时间为 O(n)。
  总时间 = O(1)+max(O(n^2),O(n))=O(n^2)。

​常见场景

• 条件分支中的时间复杂度由最坏情况分支决定。

---

2.1.5.综合应用示例

​代码片段

void example(int n) {
    // 步骤1：O(n)
    for (int i = 0; i < n; ++i) {
        // ...
    }

    // 步骤2：O(n^2)
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            // ...
        }
    }

    // 步骤3：条件判断 + 分支
    if (condition) {     // O(1)
        // S1：O(n)
        for (int k = 0; k < n; ++k) {
            // ...
        }
    } else {
        // S2：O(1)
        // ...
    }
}

​时间复杂度分析

1. ​步骤1：O(n)
2. ​步骤2：O(n^2)
3. ​步骤3：O(1)+max(O(n),O(1))=O(n)
4. ​总时间：O(n)+O(n^2)+O(n)=O(n^2)

 3、最坏情况下分析的局限性

3.​1. 核心问题：高估实际运行时间

• ​现象：最坏情形分析（Worst-Case Analysis）可能给出过于悲观的时间复杂度，导致理论结果远大于实际需求。
• ​原因：
  • 最坏情形对应的输入在实际中极少出现​（例如恶意构造的输入）。
  • 算法的平均性能（Average-Case）可能显著优于最坏情形，但平均分析复杂度高或尚未解决。

3.​2. 解决方向

• ​收紧分析（Tighten the Analysis）​：
  通过更精细的观察（如利用输入的特殊性质或算法隐藏的优化逻辑），缩小理论与实际的差距。

  • ​示例：快速排序的最坏时间复杂度为 O(N^2)，但实际中通过随机化选择枢轴，可达到平均 O(NlogN)。

• ​接受局限性：
  若无法改进分析，需明确最坏情形是已知的最佳理论结果，尽管它可能不够精确。

3.​3. 复杂算法的分析挑战

• ​案例1：希尔排序（Shellsort）​

  • 代码量仅约20行，但其时间复杂度分析至今未完全解决。
  • 已知某些增量序列的最坏情形为 O(N^3/2)，但精确分析仍开放。

• ​案例2：不相交集算法（Union-Find）​

  • 同样简短（约20行代码），但其时间复杂度的严格证明曾耗费数十年，最终借助均摊分析（Amortized Analysis）才得以解决。