【GNN】第五章：图神经网络架构中的基础设施——GCN、GAT、GraphSAGE、TopKPooling、GAP、GMP

【GNN】第五章：图神经网络架构中的基础设施———GCN、GAT、GraphSAGE、TopKPooling、GAP、GMP

第四章讲GCN层时，就已经给大家梳理过：一个图神经网络模型 = 基本的层结构+巧妙的架构设计，并且给大家详细讲解了一种图卷积层GCN。本篇讲图神经网络中的其他各种层，下一个篇章讲GNN领域中的一些经典架构设计。

一、图神经网络层概述

1、一个图神经网络通常是由多种层组成的多层神经网络架构。一般会包含图卷积层、池化层、线性层、激活层、归一化层、dropout层等这些DL领域的基本层结构。其中：

图卷积层是图神经网络架构中最最最核心的层。就类似于图像处理领域中的卷积层之于卷积网络架构一样。
其主要功能是重构节点或边的特征表征。就是节点或边的特征向量在图卷积层的消息传递操作中，每个特征向量接收其邻居节点的特征向量的信息，并将这些信息聚合成一个新的特征向量表示，所以说图卷积层的本质就是重构特征。

池化层是图神经网络架构中经常和图卷积层搭配的层。就类似于图像处理领域中的pooling层和conv层经常搭档一样，比如VGG的卷积+池化的经典架构设计。只是图神经网络中池化层和CNN中的池化层是有一些区别的。因为二者面对的数据结构就差异很大嘛，有区别是肯定的了。
其主要功能是降维。在池化操作中，节点表示被合并为整个图的特征表示，那我们就可以进行图级任务的预测了。

本部分主要讲图卷积层和池化层，其他层就略过了，对其他层不熟悉的同学就从0开始学吧。

二、GCN层、GAT层、GraphSAGE层

图卷积层的工作原理指的就是它的消息传递机制。最原始的图卷积层是SUM求和的传递机制；后来发展的图卷积网络GCN(上一篇章讲的)，使用了节点的度信息，用度矩阵左乘右乘邻接矩阵，就相当于是一个加权的SUM；再到后面又出现了图注意力网络GAT，在消息传递过程中引入了注意力机制；目前的SOTA模型研究也都专注在消息传递机制的研究。

所以我们学习各种变异的图卷积层，就是学这些层的消息传递机制。

1、GCN
详见【GNN】第四章：图卷积层GCN_gcn图卷积网络左乘-CSDN博客

2、GAT
（1）论文下载地址： https://arxiv.org/pdf/1710.10903
（2）GAT，图注意力网络，很多博文都叫你类比Transformer中的attention机制：【NLP】第五章：注意力机制Attention_qkt公式-CSDN博客 但是我想说二者区别非常大，所以就各学各的吧，越类比越糊涂。

（3）先说结论：GAT的attention核心思想是重构图的邻接矩阵的，但不是重构图的拓扑结构，而是寻找邻居节点之间的注意力分值的，你可以理解为学习图中的边的权重的。这个权重就是attention coefficient,也就是注意力分数。然后把这个注意力分数矩阵当作图的邻接矩阵，走普通的聚合计算就完事了。

（4）GAT原理：

市面上所有资料都是对着这个计算公式长篇大论，但就没有一个人用一个小例子具体展示一下整个流程，所以当你根据它的长篇大论自己coding去实现的时候，就非常尴尬，就怎么算都和pytorch_gometirc的计算结果不一样！！！

但从公式上看，其实也没啥，hi,hj就表示节点i的特征向量和节点j的特征向量，然后通过参数w对hi和hj进行线性变换，然后拼接concatanate线性变换后的hi和hj，然后再用一个参数a再线性变换，然后再LeakyReLU，然后再softmax，就得到节点i和节点j之间的注意力分值aij了。
但是，这里面坑非常多，有些中间环节很诡异，而且市面上凡是自己coding出来的，都是基于自己的理解coding的，所以是各说各的，大家也都不和pytorch_geometirc对答案，所以也没人追究到底对不对。

我个人认为GAT的难点不是计算公式，而是作者把公式和代码实现混在一起说，讲公式的时候一直强调代码是怎么实现的，这样写代码可以并行处理、怎么怎么地高效，反而不知道在计算啥了。就是中间有太多的代码实现技巧，导致它的计算目的谜之神秘。我也是反反复复修改了好几种coding实现方式才和pytorch_geometric的运行结果一样，下面展示一下我的计算过程。

（5）GAT的实现过程：
下面我先调用pytorch_geometirc的GAT层，用调包的方式计算一下结果。然后再根据自己对上面公式的理解，手动算一下，看二者是否一样。
第一步：创建数据：

第二步：调包实现一下：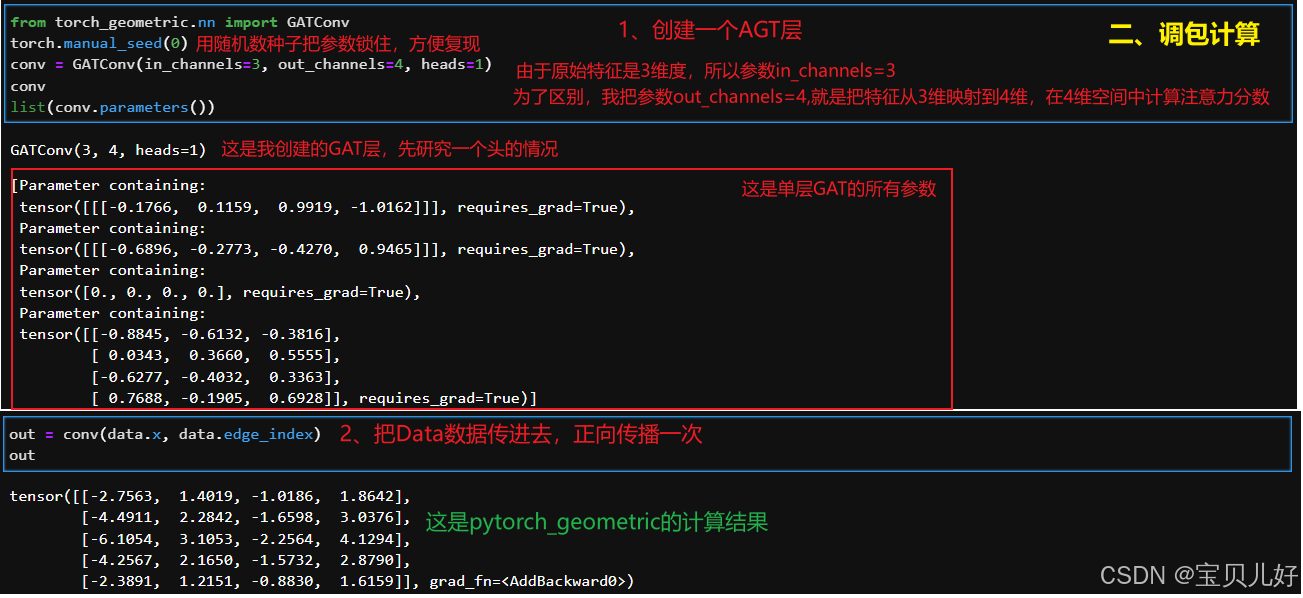

第三步：我手动计算一下，看和pytorch_geometirc的计算结果是否一致：

上面手动计算过程中，最难理解的就是第五步！现在我们再回头品味第五步，我的理解是：

这么一解读，也真是大道至简，没有什么玄乎的地方。但是这个算法就是耗费了我很多很多时间。因为所有市面上的资料都是计算流程和代码实现混着讲，让人老是摸不着头脑。比如上图中的两次repeat，一个repeat后还转置，一个不转置！很多资料一直强调就是这么做的，也没说为啥这样做？也没说这样做是干啥的？所以很多人看完云里雾里，要么干脆不追究了，要么直接照抄别人的代码，也没勇气改任何地方。还有的人直接就不是这种实现方式！是它自己理解的方法实现的，是先通过邻接矩阵，把所有有边的节点对儿取出来，然后根据节点对儿，concat两个节点的特征向量，然后在线性变换成一个注意力值，然后再leakyReLU->mask->softmax，我一开始也是照着这个思路coding的，但是死活和pytorch_geometric的结果不一致，就开始怀疑各个环节，甚至怀疑是不是参数没有xavier初始化，又跑去源码找pytorch是怎么初始化的，然后又找不到pytorch的初始化参数，真是搞得晕头转向的。源码是看得头晕眼花，因为包装太多层了。论文也是云里雾里，因为论文中老是原理和代码实现混搭着绕圈，功力尚浅的我实在没get到啥灵感。我一般都是已经通过别的渠道对一个算法已经有了一个非常深刻的理解了，再回头看论文看源码，来印证我的理解，而不是一知半解就能从论文或源码中看出名堂来。

牢骚就抱怨这么多吧，最后再展示一个多头的例子就结束这个话题：

GCN是频域GNN的代表，GAT是空域GNN的代表。
GAT是Bengio大佬团队出品，发表在ICLR2018，模型性能达到state-of-the-art：
一是，更具有可解释性。从我对第五步的拆解中，你就可以看到每个注意力分值都是有含义的。
二是，GAT的计算复杂度更低。
三是，计算权重时，不需要事先得到整个图拓扑结构或所有顶点的特征(只需访问目标节点的领接节点)。
四是，GCN使用度矩阵来衡量邻居节点之间的权重，这种做法虽然可以节省很多参数，但是一方面是无法适用有向图，但GAT就不存在这个问题；另一方面是也不能用于动图，比如某个图在不同时刻可能会多或者少俩节点，多或者少俩连接，这样特征向量就会发生改变，频域GCN不太能很好适应。但是GAT就可以完美应对动态图！多几个节点少几个节点，或者多几条边少几条边都无所谓，所以模型可以用于inductive learning，即使graph完全看不到completely unseen，也可以运行训练。

3、GraphSAGE
论文下载地址：https://arxiv.org/pdf/1706.02216

GraphSAGE适用于大规模图数据的嵌入学习问题，就是适用于在超大图上进行节点表征学习。

GraphSAGE的全称是Graph Sample and Aggregate，采样和聚合，所以其核心步骤就是这两步：采样（sample）与聚合（aggregate）。

（1）GraphSAGE相对于其他类型的图卷积层，有何与众不同？
GraphSAGE和其他图卷积层(比如GCN、GAT)一样，都是重构特征的，当然这个特征可以是节点的特征也可以是边的特征。

但是，比如GCN、GAT，它们有两个致命硬伤：

一是，大规模图的训练实现困难。比如数据流经一个GCN层或者GAT层，就是一张图中的所有节点的邻接矩阵和所有节点的特征向量之间的矩阵乘。如果一张数百万节点的图，岂不是无法承受的计算之痛，常规操作几乎无法实现。

二是，GCN在引入新的节点或者需要迁移到完全新的图上，则必须对整个图进行重新训练。！因为引入新节点或者迁移到新图上，就意味着邻接矩阵、度矩阵都跟着发生相应的改变，在新的聚合结果下，原来的模型参数未必就是损失最小的那组参数，所以就得重新开始训练模型。

这种局限在动态图、快速扩展的大规模图场景中难以满足实际需求。

这两大问题凸显了GCN、GAT等这些卷积层在大规模图数据上的局限性和在动态图、快速扩展的大规模图场景中难以有效，于是GraphSAGE就带着解决这两个问题的使命诞生了。

GraphSAGE提出了一种面向大规模图数据的归纳式表示学习框架。就是通过从节点的局部邻域中采样和聚合特征来学习一个生成嵌入的通用函数。这样我想生成哪个节点的嵌入我就可以通过这个函数生成了。而不是GCN那样，一次性把所有节点的嵌入都生成。

GraphSAGE的通用框架也叫：采样和聚合归纳节点嵌入。就是将随机采样和聚合操作嵌入到模型训练中，模型学的就是一个归纳框架。模型不只是对已见过的节点进行嵌入学习，而是学习一个从节点特征及邻域结构到节点嵌入的通用映射函数。这样，当有新节点加入或者切换新数据集时，无需重新训练整体模型，只需将新节点的特征和局部邻域信息输入该映射函数，即可快速得到该节点的表示，为动态场景和实时决策提供灵活而高效的解决方案。

GraphSAGE 的思想可以概括为三个步骤：采样（Sample）→ 聚合（Aggregate）→ 更新（Update）。

采样（Sample）：对于目标节点 ( v )，从其邻居集中随机采样一定数量的邻居节点（可多阶采样，如一阶邻居、二阶邻居等）。采样是关键，因为对大规模图进行全邻域计算不仅昂贵，而且不利于并行和分批（mini-batch）训练。

聚合（Aggregate）：对采样到的邻居节点嵌入进行聚合。此处的聚合函数（Aggregator）非常灵活，可以是简单的均值，也可以是更复杂的池化（Pooling）或者基于 LSTM 的聚合操作。

更新（Update）：将目标节点自身的特征向量与聚合后的邻居信息通过某种形式（如拼接后通过全连接层，或与邻域表示进行非线性变换）加权组合，从而获得目标节点新的嵌入表示。通过多层迭代，可获取更高阶邻域信息的整合，从而丰富节点的语义表示。

（2）GraphSAGE计算原理

从公式上看非常简单，其实实现起来非常复杂，有很多很多细节要考虑，其中最重要的是采用策略和聚合函数的设计和选择。
下面这篇博文讲得非常通俗，建议大家直接跳转查看，我这里就不写了：
https://blog.csdn.net/weixin_45636780/article/details/127729633?ops_request_misc=&request_id=&biz_id=102&utm_term=GraphSAGE&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-4-127729633.142^v102^pc_search_result_base7&spm=1018.2226.3001.4187

（3）GraphSAGE在PyG中的实现

数据流的计算过程我就无法复现了，因为要先找出每个节点的邻接，然后还得随机选择n个，不够n个的就有放回的随机选，然后计算n个邻居的均值，然后计算这n个邻居的邻居，重复上面的random choice，然后mean，最后再w2线性变换。然后再和当前节点w1线性变换后相加。非常麻烦，而且很多环节都有随机性，所以复现的难度比较大。

三、池化层

池化的本质就是降维，但有的地方也叫剪枝操作，anyway，怎么叫不重要，重要的是看清它的本质。

图神经网络中的池化层的核心功能就是通过降采样来捕捉更全局的信息，然后通过全连接层、激活层进行特征融合和分类。

池化层在图级别的分类任务中非常常见。为什么？对深度学习熟悉的同学不用说就能悟了。图神经网络中正向传播的是节点或边的特征向量，如果你的任务是图级别分类任务，那可不得不断聚合所有节点和边到图的类别个数个，才能分类么。这就和图片分类任务一样，做图片分类的架构中是不是都有pooling层？！道理是一样的。

所以，根据不同的场景需求，池化层也有好多种类型，其中最常见的池化层就是：TopKPooling、global_mean_pool(GAP)、global_max_pool(GMP)

1、TopKPooling池化层
topk，从字面上就能猜到，就是把不重要的节点剔除掉，然后前K个重要节点重新组合成一个新的图，具体计算过程：
 从官网的公式上看非常得晦涩，网上很多资料都是根据上面右图的小例子来解释的，直观清晰。右图的小例子是原论文中的例子。
（1）A表示有4个节点，每个节点是一个5维的特征向量。B自然就是节点的邻接矩阵了，4x4的一个邻接矩阵。
（2）TopKPooling的目的就是把A变成A'',这样是不是就降维了，或者说剪枝了，或者说裁剪了。那A变成了A''，那A对应的邻接矩阵B也相应的变成了B''了。是不是就完美降维了。

（3）那么，A如何变成A''? B如何变成B''?
TopKPooling层其实就是一个可训练的线性层，就是上图的C，线性层的参数矩阵是5x1的形状，A经过C就被映射乘4x1了，就是D，你可以把D理解成得分，那再根据D排序得到前K个最大得分对应的节点的索引，比如上图的E处，得到的就是Top2个最大得分的索引号0和2。意思就是我们只要索引号是0、2的节点，索引是1、3的节点就丢掉了，就是剪枝剪掉了。那我们把索引是0和2的两个节点特征取出来就是F。对应的把邻接矩阵B中的那两个节点也拿出来就是B'。

但是TopKPooling层不是直接输出节点0和节点2的原始特征向量，而是先将top2的E进行sigmoid映射一下，这样分值大的就愈大，分值小的就愈小，然后根据E'的大小让节点0和节点2的原始特征放缩一下输出A'',这个A''就是TopKPooling的结果。
B'到B''就是根据索引拿出来即可。

这样我们就把节点A变成了A''，对应的邻接矩阵从B变成了B'',就实现了TopKPooling的剪枝操作了。也所以TopKPooling层的输入是一张图的所有节点和邻接矩阵，输出是这张图的ratio比例个节点和对应的邻接矩阵。一般情况下，我们都是指定ratio是0.8、0.6、0.4等，这样一点减少。

试想，当我们一层层TopKPooling后，一张图的所有原始节点就被一次次ratio比例个裁剪掉了。如果最终如果能被剪成一个节点时，那这个节点的特征就代表了它所在的图的特征。那我们就能拿着这个特征来对图进行分类或回归了。

说明：上图左边的计算公式是用tanh函数映射节点分值的，右边流程图上却是用sigmoid函数来映射的。说明这个操作是我们自己可以选择的，你就可以根据你自己数据的效果来选择你的映射函数。

2、global_mean_pool(GAP)和global_max_pool(GMP)
GAP叫全局平均池化，GMP叫全局最大池化。

为什么会有这两个池化操作？显然上面的TopKPooling是在卷积的过程中使用的，当被卷积了好几次后，最终我们是希望得到一个特征向量来表示图的，ratio肯定是用着不方便，我们一般都是在最后一个图卷积层后面接一个GAP或者GMP就完事了。这和图片卷积的思路一模一样的，比如VGG，都是这个套路。
所以这两个层非常非常容易理解：

此时就可以高枕无忧地再往后面串联线性层进行图分类或图回归了。

小结：
图卷积层是用于重构节点特征的。节点经过一个卷积层，其特征就根据邻居节点(或者说网络的拓扑结构)重构了一次。
每种类型的图卷积层(GCN\GAT\GraphSAGE)都有自己的算法和适用的地方，但它们之间并不是互不相干或者互相排斥的。在实际应用中，我们要根据图的分布、特征信息以及任务需求，来选最合适的卷积层，这样才能更有效地学习图结构数据。

TopKPooling一般跟在图卷积层后面，用于剪掉不重要的节点。所以在图神经网络架构中一般都是串联n个(图卷积+TopKPooling)这样的子架构。你就和经典架构VGG类比就好了。
global_mean_pool或者global_max_pool(GMP)一般都是串联在最后一个图卷积层的后面的**，用于生成图级特征的。

图级特征生成后，后面一般都是再串联 一到两个线性层，用于图分类或图回归的。

这也是自建图神经网络的基本思路。