蓝桥杯备赛(搜索)
·DFS基础&回溯
回溯法简介
回溯法一般使用DFS(深度优先搜索)实现,DFS是一种遍历或搜索图、树或图像等数据结
构的算法,当然这个图、树未必要存储下来(隐式处理就是回溯法),常见的是通过某种关系构造出的搜索树,搜索树一般是排列型搜索树(总节点个数一般为n!级别)和子集型搜索树(总节点个数一般为2^n级别)。
排列型就是每次枚举选哪个,子集型就是对于每一个元素选或不选(结果与顺序无关)。
DFS从起始节点开始,沿着一条路径尽可能深入地搜索(一条路走到黑),直到无法继续为
止,然后回溯到前一个节点,继续探索其他路径,直到遍历完整个图或树。
DFS使用栈或递归来管理节点的遍历顺序,一般使用递归。
很多时候DFS和回溯法不必过度区分。
排列树图解

子集树图解

回溯法模板

这是一个排列型搜索树,实际上的回溯法比较灵活,需要根据题意要求来具体分析。
vis[i]表示数字i是否使用过,也经常被用于表示某个元素是否使用过。
a[]存放结果,当dep深度=n+1时说明n层都已经算完了,直接输出结果。
子集型搜索树模板结构类似,就是在往下走时候只有两条边,表示“选或不选当前这个元素”。
例题讲解
(1)

首先可以肯定的是,每一行必然有且仅有一个皇后(因为不可能出现两个皇后在同一行),于是就通过枚举每一层皇后的位置来搜索所有可能解即可。
每放置一个皇后就将对应的米字型区域设置为“禁区”,后面的皇后就不能放在“禁区”里,回溯的时候将禁区取消掉。为了正确维护“禁区”,不能使用bool数组来表示禁区,需要使用int数组,表示这个位置被“多少个皇后占用了”,当占用数为0时表示“禁区解除”。
层数到n+1时表示找到了一个解,不可行的解都到不了第n+1层。
代码如下:
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int n = 15;
int n, ans;
int vis[N][N];//表示被多少个皇后占用
void dfs(int dep)
{
if(dep == n + 1)
{
ans ++;
return;
}
for(int i = 1; i <= n; ++ i)
{
if(vis[dep][i])continue;
for(int _i = 1; _i <= n; ++ _i)vis[_i][i] ++;
for(int _i = dep; _j = i; _i >= 1 && _j >= 1; -- _i, -- _j)vis[_i][_j] ++;
for(int _i = dep; _j = i; _i <= n && _j >= 1; ++ _i, -- _j)vis[_i][_j] ++;
for(int _i = dep; _j = i; _i >= 1 && _j <= n; -- _i, ++ _j)vis[_i][_j] ++;
for(int _i = dep; _j = i; _i <= n && _j <= n; ++ _i, ++ _j)vis[_i][_j] ++;
dfs(dep + 1);
for(int _i = 1; _i <= n; ++ _i)vis[_i][i] --;
for(int _i = dep; _j = i; _i >= 1 && _j >= 1; -- _i, -- _j)vis[_i][_j] --;
for(int _i = dep; _j = i; _i <= n && _j >= 1; ++ _i, -- _j)vis[_i][_j] --;
for(int _i = dep; _j = i; _i >= 1 && _j <= n; -- _i, ++ _j)vis[_i][_j] --;
for(int _i = dep; _j = i; _i <= n && _j <= n; ++ _i, ++ _j)vis[_i][_j] --;
int main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin >> n;
dfs(1);
cout << ans << '\n';
return 0;
}(2)
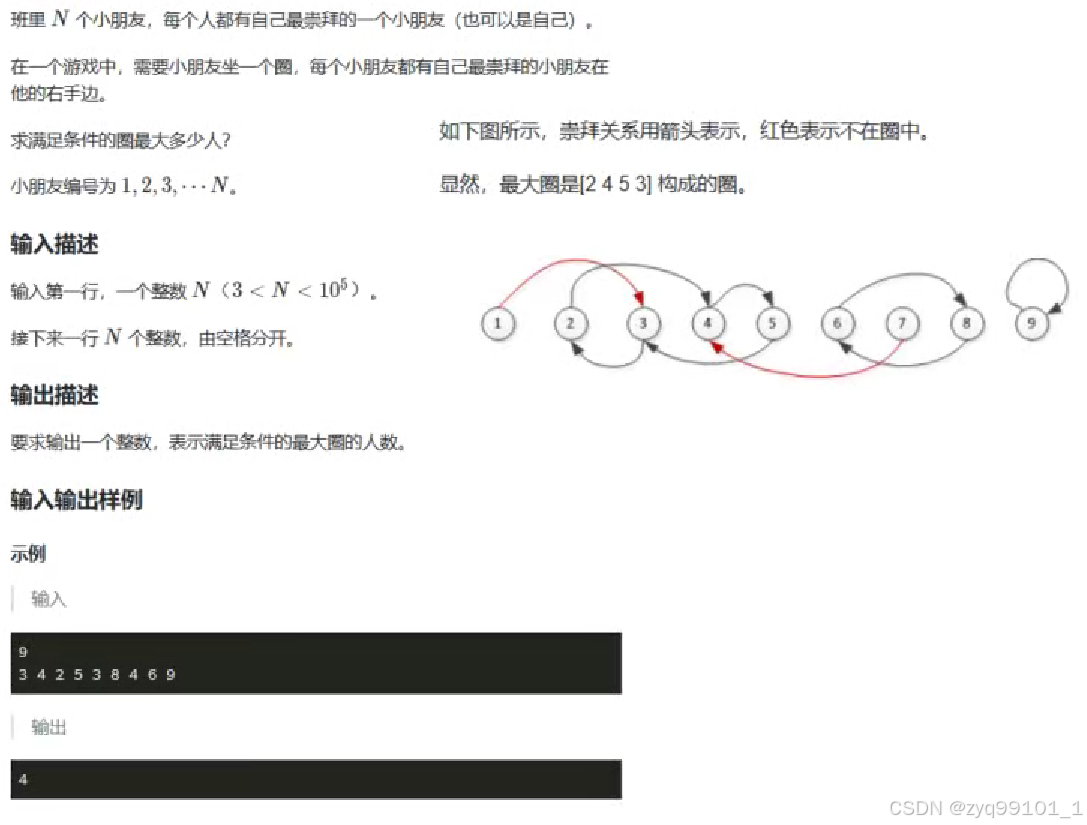
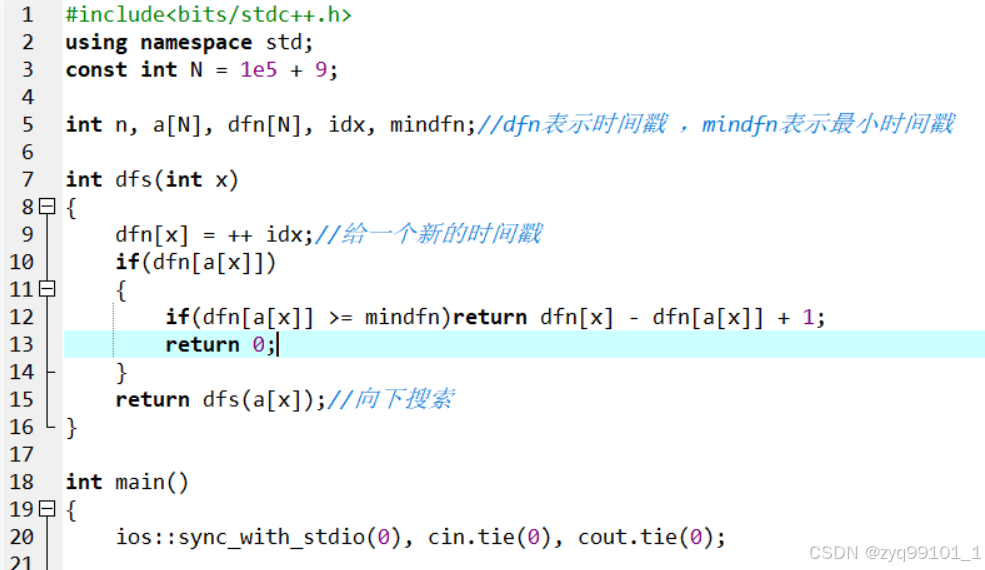
跑dfs求最大的环,可以用时间戳 ( dfn ) ,将走过的地方标记一个时间戳(即第几步走到的)。
后续搜索中,每次开始时更新最小时间戳 ( mindfn ) ,如果走到已经走过的点就必须停下,然后根据时间戳的合法性来更新最大值。
代码如下:

(3)



先用dfs将不同的岛屿染上不同的颜色,然后计算最后剩下的岛屿的颜色有多少和原先总岛屿数(即颜色数)减去剩余颜色数,得到的就是淹没的岛屿数量。需要考虑的细节较多,自己多加理解
代码如下:




·剪枝
所谓剪枝
其实就是将搜索过程当中一些不必要的部分直接剔除掉,因为搜索过程构成了一棵树,刷除不必要的部分,就像是在树上将树枝剪掉,故名剪枝。
剪枝是回测法的一种重要优化手段,方法往往先写一个暴力搜索,然后找到某些特殊的数学关系,或者逻辑关系,通过它们的约束让搜索树尽可能浅而小,从而达到降低时间复杂度的目的。
一般来说,剪枝的复杂度难以计算。
例题
lanqiao OJ 2942数字王国之军训排队

因为n比较小,所以我们可以从小到大枚举“最少队伍的数量”,然后再判断在这个队伍数量的情况下,是否可以成功分组。
这个判断合法性的函数就用搜索来实现,具体地来说,就是确定总队伍数量,然后对于每一个人,枚举他所属的队伍,用回溯法解决。
剪枝策略是,当某个人进入队伍时直接检查是否存在信系,如果存在就直接跳过。
错误展示(未剪枝):



正确代码修正:

lanqiao OJ 3008特殊的多边形


不妨规定我们构造出的3元组是递增的,那么在搜索过程中我们就可以通过计算得到当前这个位置的上限(剪枝的关键)。dfs过程中记录乘积,因为乘得越多数字越大,当乘积mul>1e6时直接返回(乘积很容易就超过1e5,数字较大时层数就两三层)。
同时还能记录一下 n - 1 条边的长度和sum,最后一条边必须小于sum。
最后用前缀和快速进行区间查询。
代码示例:

lanqiao OJ 3075特殊的多边形

不妨规定我们构造出的n元组是递增的,那么在搜索过程中我们就可以通过计算得到当前这个位置的上限(剪枝的关键)。dfs过程中记录乘积,因为乘得越多数字越大,当乘积mul>1e5时直接返回(乘积很容易就超过1e5,数字较大时层数就两三层)。
同时还能记录一下n-1条边的长度和sum,最后一条边必须小于sum。
最后用前缀和快速进行区间查询。
代码示例:


·记忆化
所谓记忆化
就是将搜索过程中会重复计算且结果相同的部分保存下来,作为一个状态,下次访问到这个状态时直接将这个子搜索的结果返回,而不需要再重新算一遍。
通常会使用数组或map来进行记忆化,下标一般和dfs的参数表对应。
注意使用记忆化需要保证重复计算的结果是相同的,否则可能产生数据失真。
斐波那契数列

如果直接采用递归来做,时间复杂度将接近O(2^n),但是我们会发现有大部分的重复计算,比如F[n-2]在求F[n]的时候算过,在求F[n-1]的时候又被算了一次,而F[1]计算次数更多了,但它们在重复计算的时候的结果是相同的,所以可以采用记忆化(也叫带备忘录的搜索)。
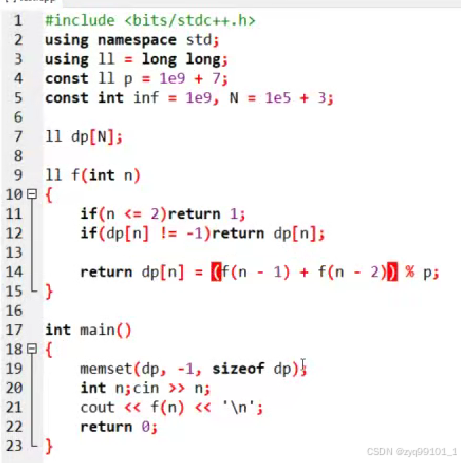
第19行对dp进行初始化,初始化为-1,指这个状态还没有被算过;当dp[n]不是-1时说明之前已经被算过,可以返回 dp[n]
lanqiao OJ 3820 混境之地5




错误代码示例(没用记忆):



正确代码示例:


lanqiao OJ 216 地宫取宝


直接写搜索是会超时的,因为这个地图其实也不小了。首先进行一个条件转换:格子中的宝贝价值比手中任意宝贝价值都大=>格子中的宝贝价值大于手中宝贝价值的最大值。
我们记录这个最大值为mx,手中宝贝个数为cnt,于是就可以设置状态dp[x][y][mx][cnt]表示走到(x,y),手中有cnt个宝贝,且最大值为mx的方案数。



