整除分块 (+例题变形K-取模 2022年天梯赛（GPLT）上海理工大学校内选拔赛)

整除分块

K-取模 2022年中国高校计算机大赛-团队程序设计天梯赛（GPLT）上海理工大学校内选拔赛

这本是一道取模的题目，运用数学公式转换，便可以用整除分块解决。

---

先介绍一下整除分块

以20为例，一共出现了多少个i的倍数？

$i$	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
$\frac{n}{i}$	20	10	6	5	4	3	2	2	2	2	1	1	1	1	1	1	1	1	1	1

可以发现在连续的一段区间内是相同的，那么就启发我们是否可以将其分为若干块分别进行计算呢?

这就是整除分块的核心思想了。

n/i 表示n里面出现了几个 i 的倍数。
也就是在n个里面，每i个为一组，可以分n/i 组，每组里有一个i的倍数

当然会有剩余的。

如果再用 n 除以 n/i ，便是如果分为 n/i 组，那么每组应该有 n/(n/i) =x 个
注意：每次都是向下取整

即x个数字为一组，会有 n/i组（当然也有剩余），也就是这x个都至少有 n/i个倍数

那么区间【i，x】，倍数皆为 n/i

总结：

利用除法的性质，将问题分解为若干个块，每个块内的值相同，从而减少计算量。整除分块在解决一些数学问题时非常有效，特别是当问题涉及到大量除法操作时，它可以大大减少计算时间。

题意

计算${\sum }_{i=1}^n(n\%i)$

因为答案可能很大，因此只需要输出答案需要对998244353取模后的结果

思路

赛时一直从规律入手，打表，废了太长时间。应该从变化数学公式、整除分块入手。

且看以下推导（懒得用latex）：

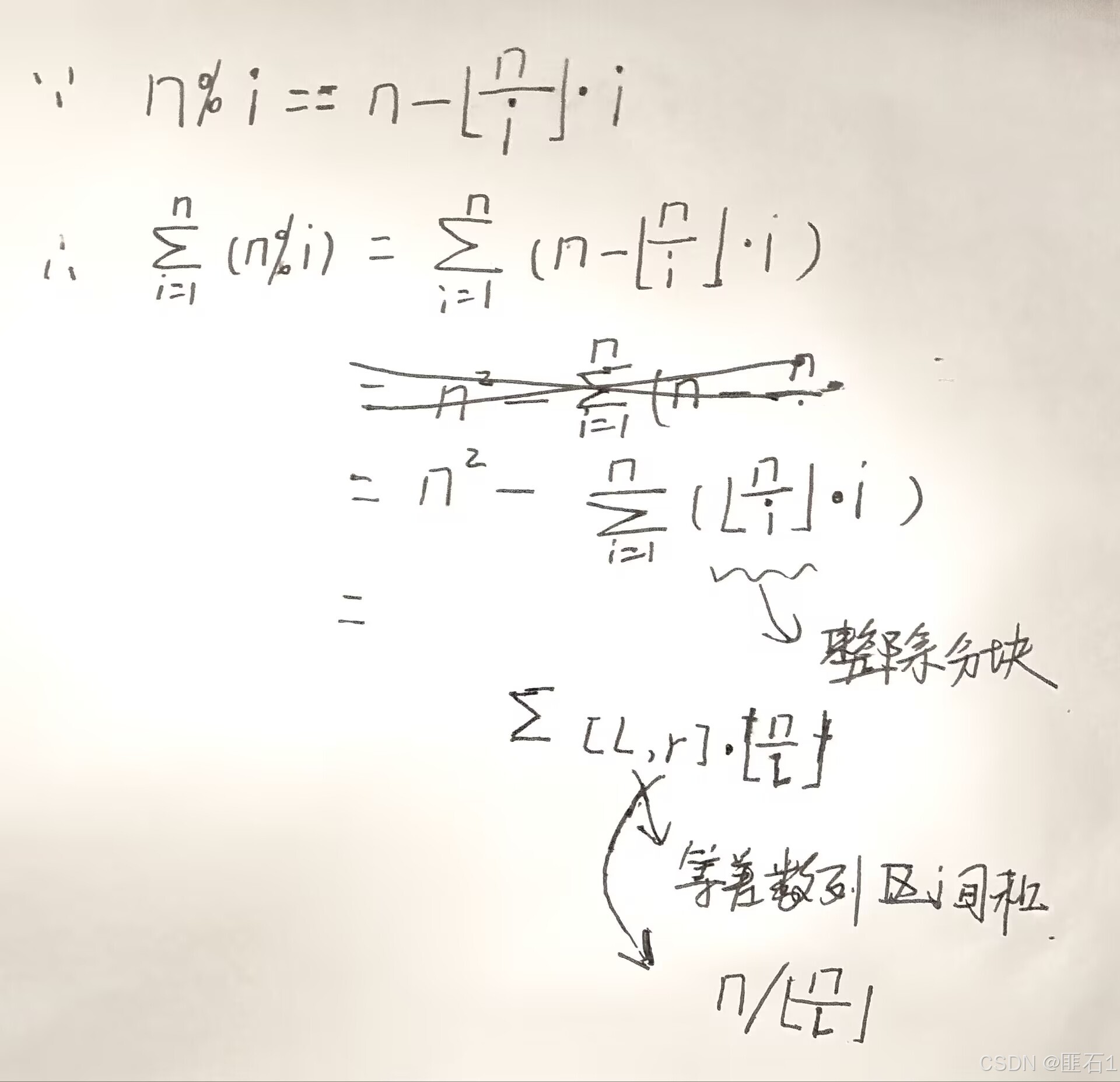
代码

void solve()
{
    int n,ans=0;
    cin>>n;
    ans=(n%mod)*(n%mod)%mod;//n^2
    __int128 i=1,j=1;//区间和会超longlong,int128最大值最高位2^127-1，不会溢出
    while(i<=n)
    {
        j=min ((__int128)n,n/(n/i));
        ans=(ans-((i+j)*(j-i+1)/2%mod*((n/i)%mod)%mod)+mod)%mod;//多取模
        i=j+1;
    }
    cout<<ans<<'\n';
}

感谢亓boyan的整除分块启蒙