Diffie-Hellman协议简单介绍
文章目录
- 1. 介绍
- 2. 数学背景介绍
- 2.1 幂模运算
- 2.2 幂模的结合律
- 3. DHKE协议过程
- 4. 中间人攻击
- 原文
- UPD
1. 介绍
Diffie-Hellman协议是一种公钥协议,用于对称密钥的分发问题。
2. 数学背景介绍
2.1 幂模运算
就是一个数的多少次幂对另一个数取模
c
=
b
e
m
o
d
m
c = b^{e} \bmod m
c=bemodm
c
c
c就叫作
b
b
b的
e
e
e次方对整数
m
m
m的模。
公钥体系一般都基于计算简单的单向性;
什么意思呢? 就是如果你知道 b b b和 e e e求 c c c是容易的,而如果你知道 b b b和 c c c反过来求 e e e则是很困难的。
因此我们就可以利用这个特性来实现公钥体系。
2.2 幂模的结合律
( c b m o d p ) a ≡ c a b ≡ c b a ≡ ( c a m o d p ) b ( m o d p ) (c^b\ \bmod\ p)^a \equiv c^{a^b} \equiv c^{b^a}\equiv (c^{a} \bmod p)^b \quad (\ \bmod\ p) (cb mod p)a≡cab≡cba≡(camodp)b( mod p)
3. DHKE协议过程
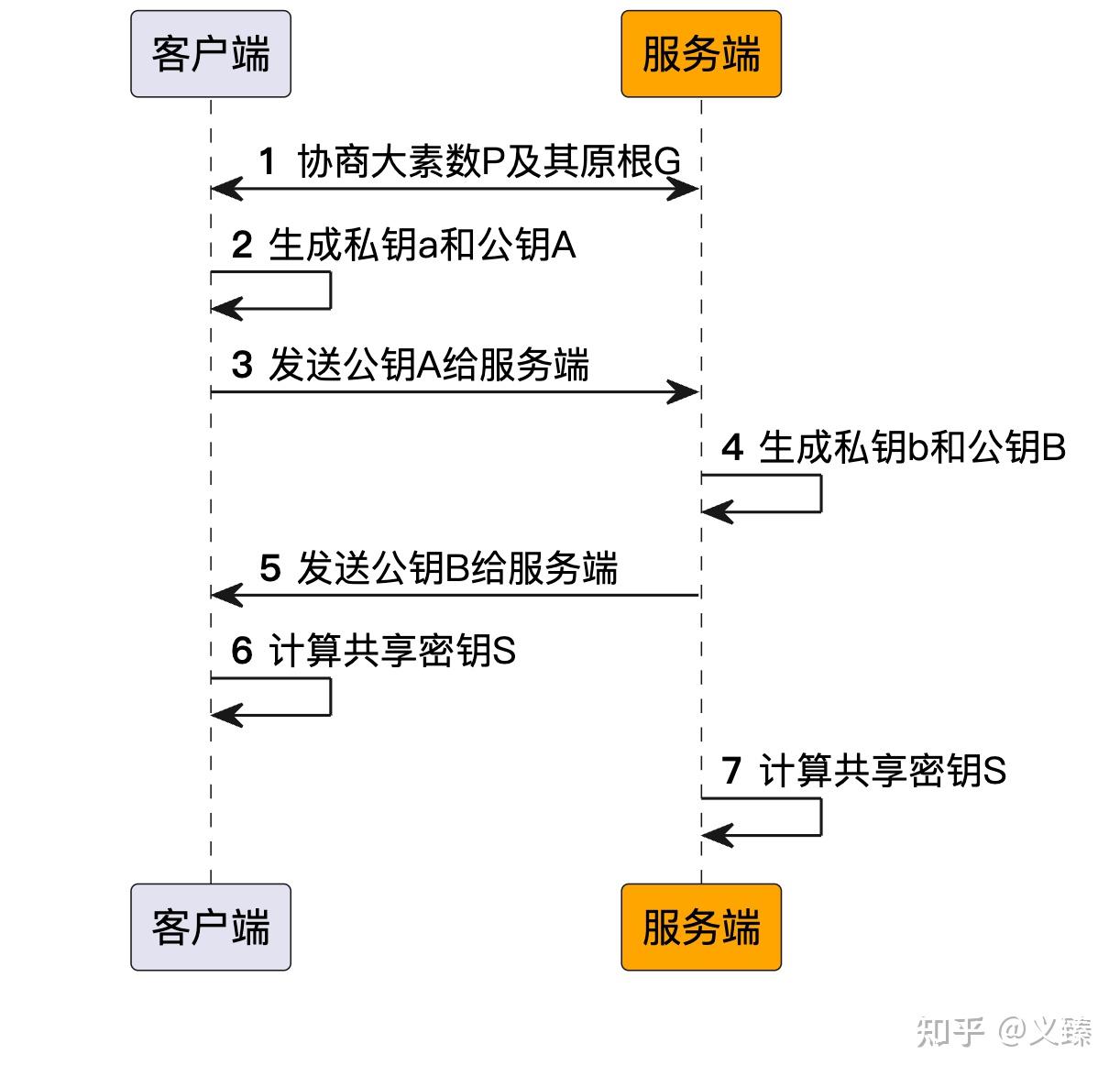
- 协商大素数 P P P和原根 G G G
- 客户端生成私钥
a
a
a和公钥
A
A
A
- A = G a m o d p A=G^a\ \bmod\ p A=Ga mod p
- 服务端生成私钥
b
b
b和公钥
B
B
B
- B = G b m o d p B=G^b\ \bmod\ p B=Gb mod p
- 客户端发送自己的公钥 A A A
- 服务端发送自己的公钥 B B B
- 客户端根据自己私钥
a
a
a和服务端公钥
B
B
B计算共享密钥
S 1 = B a m o d P S1=B^a\ \bmod P S1=Ba modP - 服务端根据自己私钥
b
b
b和客户端公钥
A
A
A计算共享密钥
S 2 = A b m o d P S2=A^b\ \bmod P S2=Ab modP
根据上面的幂模性质,我们可以知道 S 1 = S = S 2 S1=S=S2 S1=S=S2,由此共享密钥也被计算出来。
4. 中间人攻击
公钥体系并不能完全保证安全,因为可能存在一个中间人截获了大素数
P
P
P和原根
G
G
G,
再分发两把公钥,和两个人分别建立通信。

原文
zhihu-yizhen
UPD
证明幂模性质待补充
