求递增子序列LIS的两种方法

---

前言

提示：这里可以添加本文要记录的大概内容：

在开始讲解算法之前，我们先明确LIS的定义。

子序列：从一个序列中挑选一些元素（不要求连续），但必须保持原始相对顺序。例如，对于序列 [10, 9, 2, 5]，[10, 2] 和 [9, 5] 都是子序列。
严格递增：子序列中的每个元素必须比前一个元素严格大。例如，[1, 3, 5] 是严格递增的，但 [1, 3, 3] 不是（因为有相等的情况）。
LIS问题：给定一个序列，找出其中最长的严格递增子序列的长度。
示例：

输入序列：[10, 9, 2, 5, 3, 7, 101, 18]
可能的递增子序列：
[10, 101]（长度 2）
[2, 5, 7, 101]（长度 4）
[2, 3, 7, 18]（长度 4）
答案：最长递增子序列的长度为 4。
接下来，我们将详细介绍两种方法来解决这个问题
并且给出多道例题进行讲解

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、普通动态规划（DP）求解LIS

1.DP思路

动态规划（DP）是一种通过将大问题分解为小问题来求解的方法。对于LIS，我们可以用DP逐步计算出每个位置的最优解，最终得到全局最优解。核心思想是：对于每个元素，考虑它能接在哪些之前的元素后面，形成更长的递增子序列

2.DP的状态定义与转移方程

状态定义：
定义 dp[i] 表示以 第 i 个元素 nums[i] 结尾的最长递增子序列的长度。
例如，dp[0] 表示以 nums[0] 结尾的LIS长度，dp[1] 表示以 nums[1] 结尾的LIS长度。

状态转移方程：
对于位置 i，我们需要检查它之前的所有位置 j（0 ≤ j < i）：
如果 nums[j] < nums[i]，说明 nums[i] 可以接在 nums[j] 后面，形成一个更长的递增子序列。此时，dp[i] 可以更新为 dp[j] + 1。
为了确保 dp[i] 是最大的，我们需要从所有满足条件的 j 中挑选 dp[j] 最大的值，然后加 1

dp[i] = max(dp[j] + 1) 对于所有 j < i 且 nums[j] < nums[i]  这里遍历所有可能的j情况取最大的那一种就行

如果没有满足条件的 j（即 nums[i] 比之前所有元素都小），则 dp[i] = 1，因为它自身就是一个长度为 1 的子序列。
初始化：
每个 dp[i] 初始值为 1，因为最短的递增子序列就是元素本身。
最终答案：
遍历整个 dp 数组，找到最大的 dp[i]，这就是整个序列的LIS长度

3.DP的时间与空间复杂度

时间复杂度：O(n²)！！！
外层循环遍历每个位置 i（n 次），内层循环遍历 0 到 i-1（平均 n/2 次），总复杂度为 O(n²)。

空间复杂度：O(n)
只需一个长度为 n 的 dp 数组存储状态

4.DP代码实现

#include <iostream>
#include <vector>
#include <algorithm> 

using namespace std;

int lengthOfLIS(vector<int>& nums) {
    int n = nums.size();
    if (n == 0) return 0; // 空序列返回 0
    
    vector<int> dp(n, 1); // 初始化 dp 数组，每个位置至少为 1
    int maxLen = 1;// 记录全局最大 LIS 长度
    
    for (int i = 0; i < n; i++) {以第i个元素为结尾 dp[i]
        for (int j = 0; j < i; j++) {//遍历结尾元素i前面的元素
            if (nums[j] < nums[i]) {
                dp[i] = max(dp[i], dp[j] + 1); // 更新 dp[i]
            }
        }
        maxLen = max(maxLen, dp[i]); // 更新全局最大值
    }
    return maxLen;
}

int main() {
    vector<int> nums = {10, 9, 2, 5, 3, 7, 101, 18};
    cout << "最长递增子序列长度: " << lengthOfLIS(nums) << endl; // 输出 4
    return 0;
}

5.DP的图文示例

结果总结
最终 dp 数组：[1, 1, 1, 2, 2, 3, 4, 4]
LIS 长度：4
表格字段说明
索引 i：当前处理元素的下标。
nums[i]：序列中第 i 个元素的值。
dp[i]：以 nums[i] 结尾的最长递增子序列的长度。
计算过程：描述 dp[i] 是如何从前面的 dp[j]（j < i）计算得到的。
可能的子序列示例：一个以 nums[i] 结尾的递增子序列，仅为示例，不一定是全局最优解

二、贪心 + 二分查找求解LIS

1.思路分析

普通动态规划（DP）求 LIS 的时间复杂度是 O(n²)，因为它需要比较每个元素与之前所有元素的关系。而“贪心 + 二分查找”方法通过一种更高效的方式，将复杂度降到 O(n log n)。其核心在于：

1.目标：维护一个“最优”的递增子序列（不一定是最终的 LIS），确保每个长度的子序列末尾元素尽可能小。这样，后续元素就更容易接在这个子序列后面，从而最大化 LIS 的长度。
2.工具：使用一个数组 d，其中 tails[i] 表示长度为 i+1 的递增子序列的末尾元素的最小值。
3.操作规则：！！！！！！！！！！！！！！！！！！！！！！！！！！

如果当前元素大于 tails 的最后一个元素，直接将它追加到 tails 末尾，延长子序列。
如果当前元素小于等于 tails 的最后一个元素，用二分查找找到 tails 中第一个大于等于当前元素的位置，并替换它，优化某个长度的子序列末尾
。
重要说明：d数组本身不一定是最终的 LIS，但它的长度一定等于 LIS 的长度

这是算法竞赛入门到进阶这门书的原话解释，请大家仔细理解

关键点！！！
虽然 d 的长度是正确的，但它的元素只是用来维护这个长度的工具，不一定能直接对应原始序列中的一个实际递增子序列
但长度一定是最长的递增子序列的长度！！！！！！！！！！！！！

2.贪心 + 二分的时间与空间复杂度

时间复杂度：O(n log n)
遍历序列 n 次，每次二分查找复杂度为 O(log n)。

空间复杂度：O(n)
用于存储d 数组

三. 模板题讲解

1.洛谷B3637 最长上升子序列

题目不用分析，因为题意说的很清除了，现在我给出dp和贪心+二分的两种写法

1.dp写法

#include <iostream>
#include <algorithm>
using namespace std;
int n, arr[5005];
int dp[5005] ; // 以第i个数结尾的序列长度为dp[i];
int maxlen = 1;
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> arr[i];
        dp[i] = 1;//初始化长度都为1 因为就是自己
    }

    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j < i; j++)//遍历i之前的元素
        {
            if (arr[j] < arr[i])
                dp[i] = max(dp[i], dp[j] + 1);
        }
    }

    int maxa = 0;
    for (int i = 1; i <= n; i++)
    {
        maxa = max(maxa, dp[i]);//找最大值
    }
    cout << maxa;
    return 0;
}

这样也能过，因为数据很小，n的范围我圈出来了，大家看上面的图

2.贪心+二分写法

#include <iostream>
using namespace std;
typedef long long ll;
const ll M = 1e5 + 5;
ll n, a[M], d[M], len;

void slove()
{
  cin>>n;
  for (int i = 0;i<n;i++)
  {
    cin >> a[i];
  }

  d[0]=a[0];
  len = 0;//长度为i+1 因为从0开始
  for (int i = 1;i<n;i++)//这里从1开始 因为0位置我们初始化了
  {
    if(a[i]>d[len])//直接放入即可
    {
      len++;//这个别忘记
      d[len] = a[i];
    }
    else if(a[i]<d[len])
    {
      //查找第一个大于或等于a[i]的元素
      ll pos = lower_bound(d, d + len + 1, a[i]) - d;
      d[pos] = a[i];//其实没找到也没啥 因为没找到会返回数组last的位置 
      所以这里不判断也没事 长度又没更新
    }
  }

  cout << len + 1; // 别忘记加1 因为从0开始
}

signed main()
{
  //关流 加速输入输出
  ios::sync_with_stdio(0);
  cin.tie(0);
  cout.tie(0);
  slove();
  return 0;
}

2.洛谷P3902 递增

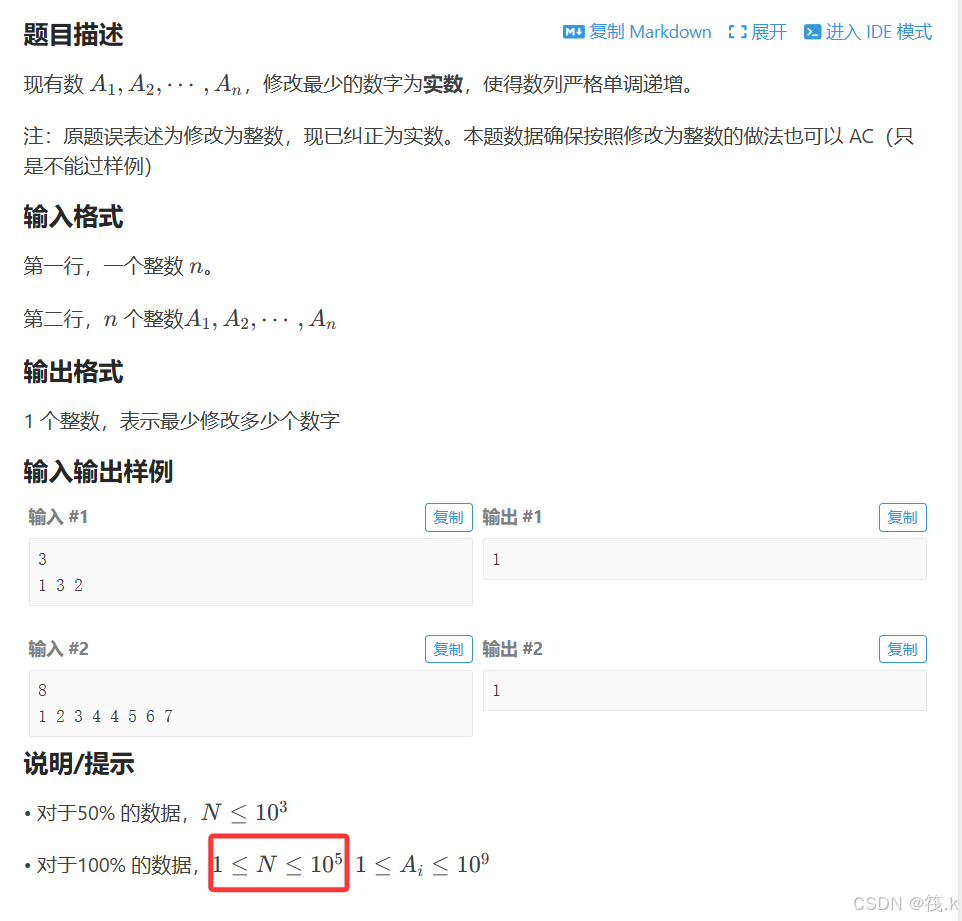
大家仔细看n最大可以到1e5，那么就不能再用dp的双重循环了
如果有网友不信邪，可以自己试试哦哈哈哈
那么这里我直接给一份贪心+二分代码

1.贪心+二分写法

#include <iostream>
using namespace std;
typedef long long ll;
const ll M = 1e5 + 5;
ll n, a[M], d[M], len;

void slove()
{
  cin>>n;
  for (int i = 0;i<n;i++)
  {
    cin >> a[i];
  }

  d[0]=a[0];
  len = 0;//长度为i+1 因为从0开始
  for (int i = 1;i<n;i++)//这里从1开始 因为0位置我们初始化了
  {
    if(a[i]>d[len])//直接放入即可
    {
      len++;//这个别忘记
      d[len] = a[i];
    }
    else if(a[i]<d[len])
    {
      //查找第一个大于或等于a[i]的元素
      ll pos = lower_bound(d, d + len + 1, a[i]) - d;
      d[pos] = a[i];//其实没找到也没啥 因为没找到会返回数组last的位置 
      所以这里不判断也没事 长度又没更新
    }
  }

  cout << n-(len + 1); // 别忘记加1 因为从0开始
}

signed main()
{
  //关流 加速输入输出
  ios::sync_with_stdio(0);
  cin.tie(0);
  cout.tie(0);
  slove();
  return 0;
}

四.练习题

1.洛谷P1091 [NOIP 2004 提高组] 合唱队形

1.思路分析

题目意思我们可以翻译为从数组中找一个点p，然后从前到这个点找一个递增子序列，从后到这个点找一个递增子序列，使得两个子序列和最大就行

全部代码我放在GitHub上了，可以点击此处进入，记得挂梯子哦

2.洛谷P1020 [NOIP 1999 提高组] 导弹拦截

1.思路分析

第一个输出很常规，就是从后往前找一个最长递增子序列，因为题目说的是找递减的，因为后面的不能比前面的大，那我们反过来求就行
但第二个输出是一个关键点！！！！！！！
问题的本质
这个问题实际上是在问：如何用最少的严格递增子序列来覆盖整个序列。根据组合数学中的一个重要定理——Dilworth 定理（在偏序集上），我们可以得出以下结论

一个序列能被划分成的最少严格递增子序列的数量，等于该序列中最长的严格递减子序列！！！

换句话说，要解决这个问题，我们需要：

1.计算序列中最长的严格递减子序列的长度。
2.这个长度就是答案

那么我们一开始说了，这道题中我们从后往前求出来的就是递增子序列，所以显而易见，求递减子序列，我们只要从前往后就行

全部代码我放在GitHub上了，可以点击此处进入，记得挂梯子哦

总结

大家可以发现 稍微难一点的都会卡n的范围，故意设置到1e5，所以这个LIS的贪心+二分的方法很有必要学习
还有就是练习题第2道的求最少多少个 递增！ 子序列可以覆盖全部数组数据的这个定理请牢记！
数组的最长严格 递减 ！子序列的长度即为数量