变分自编码器（VAE）的原理方法（二）

前文连接

说明

无论是概率人工智能爱好者、深度学习专家，还是现代人工智能领域的先驱，变分自编码器VAE 都对他们极具吸引力。它的应用范围涵盖数据生成、异常检测以及表征学习等，涉及图像、音频、文本和信号处理等多个领域。基于 VAE 的论文也经常出现在如今的 NeurIPS 会议上。在深入学习 VAE 之前，让我们先来了解一下密度估计。

七、重新审视VAE设计——数学视角

我们最后再回顾一遍，这次从最大似然估计（MLE）的角度来分析这个问题。这里会略微重复一些概念，考虑到这是一个非常复杂的话题，我觉得这样做是必要的。我们还会简单介绍一些数学知识。如果只是想了解个大概，可以跳过这部分。

让我们从头开始，也就是说，我们不要默认采用“自编码器”类型的设计。相反，让我们用数学方法逐步创建设计：

• 设输入数据集为$D=x_1,x_2\dots x_n$。我们的目标是最大化$p(x)$的对数似然值。为了最大化$log(p(x))$的总和，我们只需最大化每个单独的$log(p(x_i))$，其中i从1到n变化，$x_i$代表一个单独的观测值。有些论文在符号中使用$x_i$（和$z_i$），而另一些论文则直接使用x和z。这些都不会对计算结果产生任何影响。
• 直接处理p(x)很困难。我们使用潜在变量z来辅助处理。一旦我们知道z，就可以通过对所有z进行边缘化来获得p(x)，即对p(x|z)p(z)dz进行积分。如果z的维度较低，估计p(x)的一个简单方法是采集多个样本z _i，然后取它们的p(x|z _i )值的平均值。遗憾的是，这种方法在高维情况下行不通。因此，我们使用权重为θ 的神经网络来近似p(x|z)。我们可以将其写成p = θ (x|z)。是的，这对应于解码器。
• 所以我们需要一个z和一个θ。我们可以训练上述神经网络来获得最佳的θ。为此，我们需要一个输入、一个标签和一个损失函数。标签是原始图像x。损失函数可以通过最大似然估计 (MLE) 得到，即找到logp(x)的argmax θ，我们将在下一节中进行这部分。但是输入 z 的获取有点挑战性。对于给定的x，我们希望生成一个潜在分布p(给定x 的 z)，然后从该分布中采样以获得一个z样本作为神经网络的输入。但是p(z|x)很难生成！
• 一种方法是生成一个分布q i (z) ，该分布近似于给定第 i张图像x i 时z的分布。但是，为每张图像生成单独的q分布会变得非常复杂，因为我们的数据集非常庞大！
  相反，我们不妨创建一个新的神经网络，用参数ϕ来参数化q _i (z)的近似值，即对于所有图像， q _ϕ (z|x) ≈ q _i (z)。没错——这就是我们的编码器。我们需要它来获得一个近似分布，以便抽取样本并输入到下游解码器。因此，解码器的输入是编码器的采样输出。解码器的输出是重建的图像。标签是原始图像。
  好了，我们现在有了大致的架构。接下来我们需要做的就是通过最大化log p(x)来找到损失函数。我们通常从最大化以下函数开始：
  
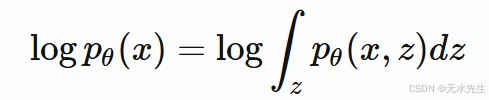
  然后我们乘以并除以 qϕ(z|x)，这使我们能够表示涉及期望的上述方程。更具体地说，我们得到：
  $$logp\theta (x)=logE[something]$$
  但我们暂且放弃这种方法，转而采用一种更简单、更直观的方法。首先，我们来计算qφ (z|x)和p(z|x)之间的差异。我们希望这个差异尽可能小。Kullback -Leibler散度 ( D _kl) 可以衡量任意两个分布之间的差异。让我们从qφ (z | x)和p(z|x)之间的D _kl的定义开始，并采取以下几个简单的步骤！
  
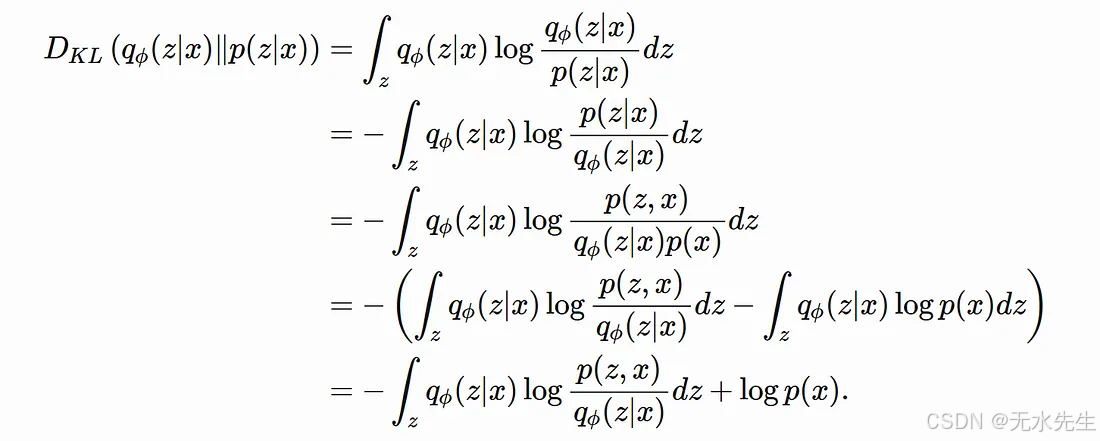
  因为对给定x的潜在z的概率分布在所有可能的z上进行积分等于 1，而对于logp(x)，它在积分中就像一个常数。

注意上面等式右侧复杂的第一项。嘿，这不就是同一个家伙吗——我们的 ELBO L。稍微调整一下，我们就得到了：

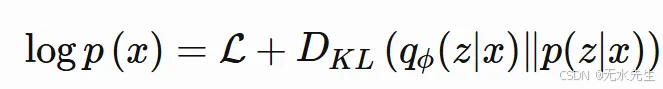
好的，所以我们需要最大化上面的方程。根据定义，任何 KL 差都是非负的。因此，L是log p(x)的自然下界，即log p(x)始终≥ L。为了最大化log p(x)，我们只需要最大化L。最大化第二项在直觉上没有意义，因为根据设计，我们的近似后验概率q(z|x)应该尽可能接近p(z|x)。因此，它们之间的 KL 差应该尽可能小。我们唯一的希望是最大化L。其他的一切都不在我们的掌控之中。让我们专注于L。

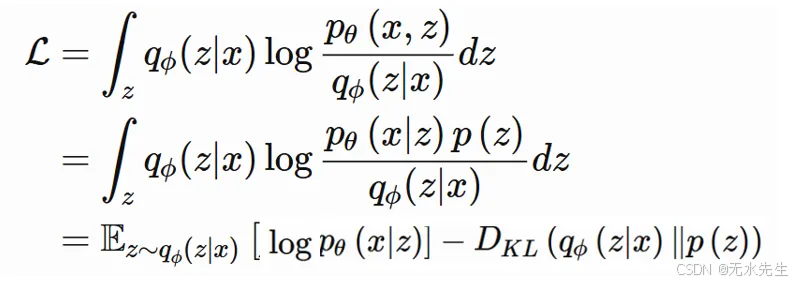
在步骤 3 中，我们将log(a*b/c)展开为loga+logb/c，再展开为loga-logc/b 。然后利用期望和D kl的定义重写方程。最终得到两项，这两项都不包含p(z|x)。这简化了我们的工作，因为p(z|x)一直难以捉摸。现在我们需要最大化上述两项关于θ和φ 的值！

第一项是我们熟悉的重构项。数学上，我们需要最大化pθ (x|z)对数似然的期望，其中pθ(x|z)是解码器的输出。对于高斯分布，这等价于最小化x和x’之间的均方误差 (MSE ) 。实现起来可能有点棘手。我们可以使用蒙特卡洛( MC ) 估计来近似这个期望。简单来说，我们从编码器的输出分布中抽取若干样本，并对这些样本的损失取平均值。第一项完成！
第二项最小化了（近似）后验分布q φ (z|x)与先验分布p θ (z)之间的 KL 散度。等等，这个p θ (z)是什么？我们之前没有讨论过它。我们讨论过p(z)，它是一个单位高斯先验。VAE论文的作者 Kingma 等人将其称为p θ (z)而不是p(z)。关于原因，请参见附录 1。简而言之，数学原理建议我们使编码器的输出尽可能接近紧凑的单位高斯分布，这样潜在画布就不会有任何间隙。

• 我们在前几节中通过理论直觉做出的推断，现在已由最大似然估计（MLE）得到证实。
• 请注意，损失函数就是 ELBO 的负值。
• 尽管我们选择p(z)和p(x|z)为简单的 Gaussian 分布，但z与神经网络最终输出之间的非线性映射导致边缘分布p(x)变得复杂，并有可能产生创造性的输出。请记住，神经网络包含像 ReLU 这样的非线性层。
• 由于真实后验分布近似呈高斯形式，因此变分近似后验分布为q φ (z|x ) = N(z; u, o² * I)，其中均值/方差组合为u和o² ，这些是权重为φ的编码器的输出。更具体地说，它们是输入x i 和变分参数φ的非线性函数。
• 让我们来看编码器的输出。它是q(z|x) = N (z; u, o²I)。这里u是编码器输出的均值，等于W2·h+b2，log(o²)是输出var的对数，等于W3·h+b3。h是什么呢？它是隐藏层的输出，等于tanh(W1·x+b1)，其中x是我们的输入。所有这些权重{W1-W3 和偏置 b1-b3}都属于φ——编码器的权重。同样地，对于解码器，所涉及的权重统称为变分参数θ。如果你和我一样好奇为什么神经网络预测的是log(var)而不是var，我猜测这是因为 log(var) 在训练过程中具有更好的数值稳定性。
• 我们可以自由选择潜在变量所需的结构。通过选择p(z)和qφ (z|x)服从高斯分布，上述损失函数中的 KL 项可以很容易地求解，从而得到闭式解！
  呼，现在只剩下计算φ和θ了——编码器和解码器的权重。我们需要对φ和θ求导并优化下界L。我们已经有了输入/输出/损失函数。可惜的是，还有一个问题需要解决——梯度下降法不起作用！

如果你还记得，我们从编码器的输出中采样Z并将其发送到解码器。Z 是采样得到的，因此是一个随机变量。不幸的是，神经网络是确定性的，如果我们向它们输入随机数据，它们在训练过程中将无法正常工作。权重无法调整，因为梯度无法通过出现这种随机性的节点。如果没有反向传播，我们就束手无策了！Kingma 的论文提供了一种确保梯度估计器可靠性的解决方案。他们通过一种重参数化技巧来实现这一点！这个技巧虽然由来已久，但在论文发表后才广为人知。详情请参见附录 2。

八、VAE推理——模型训练完成后会发生什么

通过从潜在空间（即从N(0,I)中采样）进行采样，我们可以直接将解码器 用作生成模型，从而创建与训练期间观察到的数据概念上相似的全新数据。或者，我们可以通过以下方式生成现有图像x的变体：将其传递给编码器并创建潜在分布，然后从该潜在分布中采样，并将该样本传递给解码器进行重建。

为了更精准地生成人脸，我们可以利用条件信息。例如，如果我们训练了一个基于人脸的变分自编码器（VAE），我们可以通过反复试验，在潜在空间中观察到哪些区域能够生成戴眼镜的人脸。然后，我们可以从这些区域中采样点来生成新的戴眼镜的人脸。这通常需要在已知的潜在向量之间进行插值，或者需要手动探索。稍后我们会用代码来演示一些有趣的操作。
在条件变分自编码器（Conditional VAE）中，生成过程取决于特定信息，例如类别标签、文本描述等。DALL-E 使用离散自编码器（而非连续自编码器）将图像x转换为潜在空间Z。它包含一个 Transformer 组件，用于学习“语言”与Z之间的相关性。其最终目标是学习给定文本提示的图像条件分布，即p(x|y) ，其中x是图像，y是文本提示。结合一些矢量量化和反向传播技巧，我们便得到了世界上最复杂的生成人工智能算法之一。
先从一些有趣的教程开始，比如这个、这个或者这个。
这里有一些稍微高级的变体（使用变分自编码器生成情绪面孔），或者这个变体，它实际上打开了稳定扩散管道的引擎盖，展示了其内部运作机制。
这是一个使用 VAE 作为降噪器的简单示例——例如，我们可以用它来清理和修复非数码时代的老家庭照片。

九、简化VAE设计的两个实用假设

现在让我们再次回顾一下VAE的设计，以解决一些实际问题。当我们谈到多元高斯分布的“方差”时，实际上指的是“协方差矩阵”。为了简化神经网络的计算，我们假设协方差矩阵仅在对角线上有非零值（各向同性高斯分布）。因此，编码器只需为每个潜在维度生成一个方差（以及一个均值）。可以说，这是一个合理的假设。

我们接下来的实际决策是让解码器只生成均值，而不是方差。相反，方差被作为一个超参数来处理。不仅如此，大多数实现还假设所有像素的方差相同 （此外还假设所有协方差均为 0）。从这个意义上讲，解码器的输出p(x|z)在理论上是一个有效的正态分布——每个像素都有一个均值和一个方差！大多数 VAE 博客都忽略了这些细节。我很想看到更多关于为什么方差不由解码器生成以及这一决策的影响的理论解释。更多内容请参见附录 3。

十、VAE在LLM时代的重要性

长期以来，VAE 与另一种名为 GAN 的架构在图像生成任务上展开竞争。即使在参数量高达万亿的模型时代，VAE 仍然保持着其重要性。例如，VAE 是图像生成中使用的稳定扩散模型的关键组成部分。潜在扩散的基本概念大致如下：首先，训练一个 VAE 将图像转换为紧凑的潜在表示。然后，将该潜在表示与基于训练图像的潜在表示进行训练的扩散模型相结合。我们在此处对扩散模型进行了深入讨论。

视频生成也运用了相同的概念。例如，OpenAI 的 SORA 就是利用 VAE 构建的潜在空间进行训练的。有趣的是，视频模型从零开始训练非常困难，因此它们通常使用预训练的稳定扩散 VAE 模型的权重进行初始化。由于这种方法基于图像，因此可以很好地进行“空间”压缩，但无法进行“时间”压缩。时间压缩是指基于时间的压缩。如何改进潜在压缩以更好地捕捉帧间运动是一个活跃的研究领域。

基因组编码着基因网络，这些基因网络无缝相互作用，共同维持生命体的生命活动。细菌基因组组成建模是一个热门的研究课题。为此，我们构建了基因组的简化表示。然后，我们训练了一个去噪变分自编码器（VAE），使其能够接收（故意）损坏的基因组向量并重建原始基因组。最终得到的模型DeepGenomeVector能够有效地捕捉基因组网络中复杂的依赖关系。

事实上，我们不妨看看最近一次NeurIPS大会上使用的VAE模型。没有什么比这更能体现VAE的实用性了，对吧？

P-VAE：一种具有泊松分布潜在空间的变分自编码器，展现出类似大脑的结构和功能。之所以使用泊松分布而非连续的高斯分布潜在空间，是因为大脑将输入编码为离散的脉冲计数。
LiteVAE 针对潜在扩散模型的设计利用了“二维离散小波变换”的概念来提取特征，并帮助编码器构建更好的潜在空间表示。这种方法通过促进学习更有意义的特征，简化了编码器的任务。
QVAE-Mole：为了使用量子计算生成三维形式的分子（是的！参见此处，量子计算现在已成为主流），选择 VAE 作为生成器，因为它简单且具有一次性生成能力，与经典的扩散模型相比，它更“量子友好”。
抗菌肽（AMP ）能够对抗细菌感染！然而，天然AMP的来源有限。那么，如何利用基于变分自编码器（VAE）的模型来生成AMP呢？例如，这里就使用了一种简洁的基于VAE的去噪模型，该模型以所需的理化性质为指导来生成AMP。这些理化性质（单独嵌入）指导着VAE编码器的训练过程，将具有所需性质的AMP的分布转换为标准的高斯分布！这些理化性质也被用于训练VAE的解码器，从而可以从标准的高斯分布中随机抽取样本来生成具有所需性质的AMP！VAE的概念正被用于对抗细菌！
Kingma 的论文大量使用了pθ (x)、pθ ( z)、pθ ( x,z)、pθ ( x|z) 等术语。这是否意味着所有这些分布都具有相同的参数集？显然不是！一个合理的解释是，这里使用的θ是所讨论分布的相应参数集的通用符号。

或者——这是否意味着解码器的权重θ被用来输出所有这些不同的参数？很可能不是。但这并非牵强的假设。受限玻尔兹曼机使用伯努利潜在变量，其参数在训练过程中学习得到。

第三种解释如下：Kingma 假设解码器权重θ足以生成p(x)、p(z)、p(x,z) 和 p(x|z)的参数。这是如何实现的呢？他们做了一个简单的假设：p(z)服从单位高斯分布，即为常数。因此，权重为θ 的编码器无需生成该分布的参数，因为我们知道对于单位高斯分布，θ 的均值为0，方差为 1。它只需要生成pθ (x|z)即可。此外，如果我们假设z服从单位高斯分布，那么p(x,z) 的参数就只包含x。而且，如果p(x|z)由权重为θ 的解码器参数化，那么这些权重也负责给出边缘分布p(x) 。从这个意义上讲，使用pθ (x)是可以接受的。因此p θ (x)、p θ (z)、p θ (x,z)和p θ (x|z)是合理的。

无论金马的本意是什么，这种约定俗成的做法令人困惑。

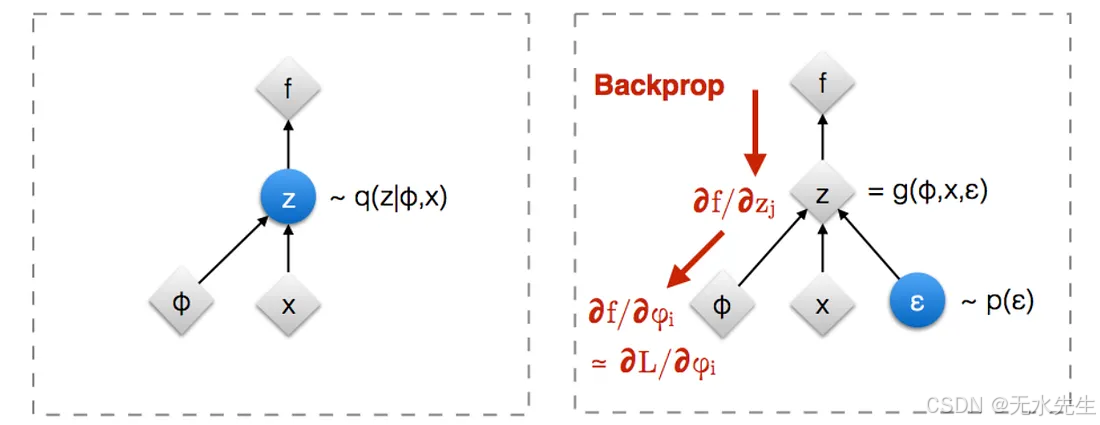
如前所述，我们的损失函数包含一个与随机变量期望值相关的项。采样并非确定性函数，因此没有导数。反向传播算法在发生采样的节点处会直接拒绝反向传播。我们该怎么办？

我们知道高斯分布有一个有趣的性质：N(Mu, Var) = Mu + Var * N(0,1)。基本上，从分布N(Mu, Var)中抽取的样本等于Mu + Var *从单位高斯分布中抽取的样本。这里，单位高斯分布就是我们进行抽样的对象。因此， Mu和Var不再是随机的。太棒了！这就是重参数化技巧，它能得到一个低方差的梯度估计器。

让我们将此应用于损失项：E z~qφ(z|x)的log p θ (x|z)。解码器的输入是来自近似后验分布z~q φ (z|x) 的随机样本。与其说z是从q φ (z|x)中采样得到的，我们可以说z是一个“函数” ，它接受 (1)单位高斯分布的样本ϵ、 (2) 均值 ( Mu ) 和(3)方差 ( Var)。该函数将ϵ的值平移（潜在分布的均值） Mu，并乘以（潜在分布的方差）Var 。该函数的输出是一个看起来像是来自z ~ q φ (z|x)的样本。Mu和Var来自编码器的上游，而ϵ来自单位高斯分布。现在，梯度反向传播的路径清晰可见！现在我们可以进行“梯度下降”来获得调整后的Mu和Var值（无需反向传播通过单位高斯样本ϵ，因为这条路径无关紧要）。详情请参见此处。

• 变分法是指一类通过将推断问题转化为优化问题来规避难以处理的积分（例如p(z|x)）的方法。“变分”一词源于“变分法”，而变分法正是处理优化问题的学科。
• VAE可能会出现后验崩溃。当编码器学习到的分布与先验分布（单位高斯分布）过于相似时，就会发生这种情况，导致潜在变量丢失关于输入的有效信息。结果，解码器主要依赖先验分布来生成图像，从而降低了模型的性能。当然，罪魁祸首是我们——我们在损失函数中添加了KL散度项，从而促使潜在空间分布与单位高斯分布相匹配。缓解后验崩溃的一个简单方法是引入超参数β，用于缩放KL散度项。这就是β-VAE。
• VQ-VAE（矢量量化）模型通过编码器学习离散的潜在变量，因为离散表示更适合语言、语音、推理等问题。矢量量化是一种将多维向量映射到有限“代码”向量集的方法。
• 我曾在某处读到，编码器输出log(var)而不是直接输出var的真正原因是为了确保神经网络不会学习到负值。由于方差是标准差的平方，它不可能为负。我们通常让网络学习log(var)，然后对这个值取指数来得到实际的方差。
  在某些情况下，变分参数是针对每个观测值单独学习的。因此，你会得到类似q φ1 (z1|x1)、q φ2 (z2|x2)等的参数——每个图像对应一个。在整个数据集上共享参数φ可以减少计算量，这被称为摊销变分推断。
• 如果像素是二值（黑白），则假设服从伯努利分布，损失函数为二值交叉熵，而不是均方误差。
• 通常，logp θ (x|z)会被原始图像像素与重建像素（解码器输出的均值）之间的均方误差 (MSE) 所取代。这等价于将所有图像的协方差矩阵设置为单位矩阵。显然，原始的数学公式在处理连续数据和高斯假设时存在一些问题。为了确保重建误差为零，最大似然估计 (MLE) 会将估计方差推向零以最大化似然值。似然值会趋于无穷大，KL 正则化器也因此失效。这可能与 β-VAE 有关。总之，这种接近于零的方差会导致过拟合，我们无法获得良好的生成模型，并且 VAE 的行为更像是一个确定性自编码器。解决方案似乎是将方差生成排除在解码器的作用域之外，并将其设置为单位矩阵或超参数。这在一定程度上缓解了数学问题，并使我们得到合理的结果。
  参考文献：