当前位置：首页 > news >正文

工作室装修网站源码wordpress 提请审批

news 2025/11/16 19:31:31

工作室装修网站源码,wordpress 提请审批,苏州小程序开发企业,优秀展示空间设计在机器学习领域，线性回归是最基础且应用广泛的预测模型之一。它通过构建属性的线性组合来拟合数据，核心目标是最小化预测值与真实值之间的误差，适用于房价预测、销量预估等多种回归问题。本文将从线性回归的基本原理出发，逐步深入…

在机器学习领域，线性回归是最基础且应用广泛的预测模型之一。它通过构建属性的线性组合来拟合数据，核心目标是最小化预测值与真实值之间的误差，适用于房价预测、销量预估等多种回归问题。本文将从线性回归的基本原理出发，逐步深入到数学推导、评估指标，并结合 Python 实战案例，帮助读者全面掌握这一经典算法。

一、线性回归简介：核心思想与模型形式

线性回归的本质是通过属性的线性组合构建预测函数，找到一条直线（二维）、平面（三维）或更高维的超平面，使该模型对数据的拟合效果最优（即预测误差最小）。

1.1 线性模型的数学形式

对于一个由d个属性描述的样本x = (x₁; x₂; ⋅⋅⋅; x_d)（其中x_i是样本在第i个属性上的取值），线性回归的预测函数可表示为：

一般形式：f(x) = w₁x₁ + w₂x₂ + ... + w_dx_d + b
向量形式：f(x) = wᵀx + b

其中：

w = (w₁; w₂; ⋅⋅⋅; w_d) 是权重向量，代表每个属性对预测结果的影响程度；
b 是偏置项（截距），用于调整模型在没有任何属性输入时的基础预测值；
wᵀ 表示w的转置，向量形式更简洁，也便于后续矩阵运算（尤其适用于多元线性回归）。

1.2 单变量与多变量线性回归

根据样本属性的数量，线性回归可分为两类：

单变量线性回归：仅含 1 个属性，模型表现为二维平面中的一条直线，例如通过 “房屋大小” 预测 “房价”，公式为 f(x) = w₀ + w₁x（w₀即b，x为房屋大小）。
多元线性回归：含 2 个及以上属性，模型表现为高维空间中的超平面，例如通过 “房屋大小、房间数、地段” 预测 “房价”，公式为 f(x) = w₀ + w₁x₁ + w₂x₂ + ... + w_nx_n。

二、模型求解：最小二乘法

线性回归的核心是找到最优的w和b，使预测值与真实值的误差最小。最常用的方法是最小二乘法，其本质是最小化 “均方误差”（对应欧氏距离）。

2.1 误差定义：均方误差

对于m个训练样本 {(x₁,y₁), (x₂,y₂), ..., (x_m,y_m)}，模型的预测值为 f(x_i) = wᵀx_i + b，真实值为y_i。
均方误差（MSE）定义为：
E(w,b) = (1/m) * Σ（从i=1到m）[y_i - f(x_i)]²

最小二乘法的目标是找到w*和b*，使E(w,b)最小化，即：
(w*, b*) = argmin（w,b）E(w,b)

2.2 数学推导：求最优参数

通过对E(w,b)求偏导并令导数为 0，可解出w和b的最优解（以单变量为例）：

对b求偏导并令其为 0，得偏置项b的最优解：
b* = ȳ - w*x̄
其中x̄ = (1/m)Σx_i（样本属性均值），ȳ = (1/m)Σy_i（样本标签均值）。
对w求偏导并令其为 0，得权重w的最优解：
w* = [Σ（从i=1到m）(x_i - x̄)(y_i - ȳ)] / [Σ（从i=1到m）(x_i - x̄)²]

对于多元线性回归，可通过矩阵运算简化求解（需满足XᵀX可逆），最终最优解为：
w* = (XᵀX)⁻¹Xᵀy
其中X是m×(d+1)的设计矩阵（每行前d列为属性值，最后 1 列为 1，用于融合偏置项b），y是m×1的标签向量。

三、模型评估：常用指标

模型训练完成后，需要通过评估指标判断拟合效果。线性回归中最核心的 3 个指标如下：

3.1 误差平方和（SSE/RSS）

定义：所有样本预测值与真实值差值的平方和，反映总误差大小。
SSE = Σ（从i=1到m）[y_i - ŷ_i]²（ŷ_i为预测值）
解读：SSE 越小，说明模型对样本的拟合误差越小，但受样本数量影响较大（样本越多，SSE 可能越大）。

3.2 均方误差（MSE）

定义：SSE 的平均值，消除了样本数量的影响，更适合跨数据集对比。
MSE = (1/m) * Σ（从i=1到m）[y_i - ŷ_i]²
解读：MSE 越小，模型泛化能力可能越强（需结合验证集判断，避免过拟合）。

3.3 决定系数（R²）

定义：衡量模型解释标签变异的能力，取值范围为(-∞, 1]。
R² = 1 - [SSE / SST]
其中SST = Σ（从i=1到m）[y_i - ȳ]²（总平方和，反映标签本身的变异程度）。
解读：
- R² = 1：模型完全拟合所有样本，预测无误差；
- R² = 0：模型预测效果等同于直接使用标签均值（无实际意义）；
- R² < 0：模型预测效果差于均值（通常是数据不符合线性假设）。
  实际应用中，R²越接近 1，模型拟合效果越好。

四、实战：用 LinearRegression 实现波士顿房价预测

波士顿房价数据集是经典的回归任务数据集，包含 506 个样本和 13 个特征（如犯罪率、平均房间数等），目标是预测房屋中位数价格。代码如下：

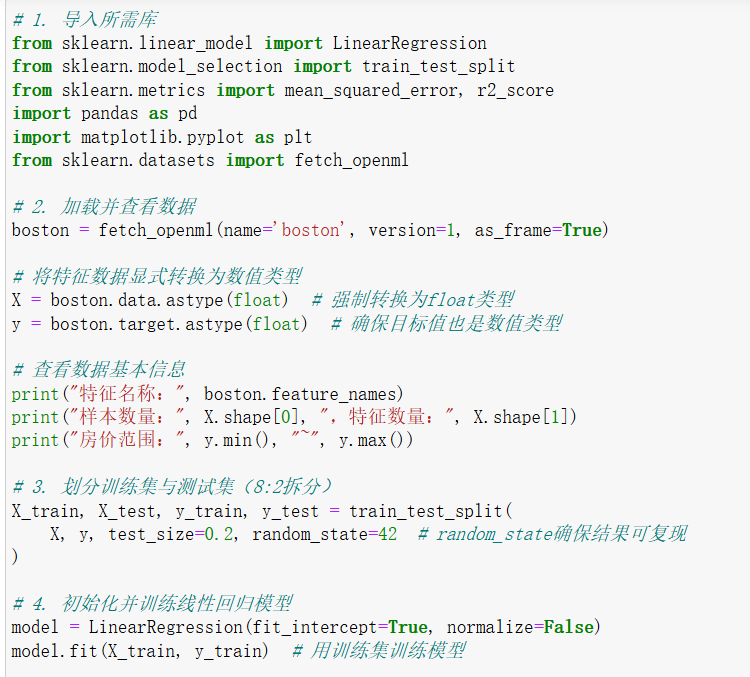
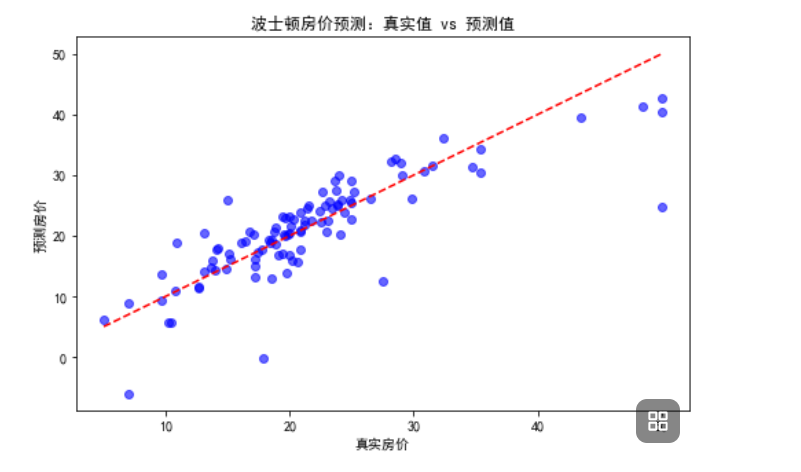
五、注意事项与拓展

数据预处理：
- 线性回归对异常值敏感，需先通过箱线图、Z-score 等方法处理异常值；
- 若特征量纲差异大（如 “房屋大小” 单位为㎡，“房间数” 为个），需先归一化（StandardScaler）或标准化（MinMaxScaler），避免权重被量纲主导。
线性假设验证：
- 需先通过散点图、相关性分析（Pearson 相关系数）验证特征与标签的线性关系；若非线性，可尝试特征工程（如平方、对数变换）或改用非线性模型（如多项式回归、决策树）。
多重共线性：
- 多元线性回归中，若特征间高度相关（如 “房屋总面积” 与 “卧室面积”），会导致XᵀX不可逆、权重不稳定，需通过 VIF（方差膨胀因子）检测并删除冗余特征。
拓展模型：
- 当数据线性关系较弱时，可使用多项式回归（通过PolynomialFeatures构建高次特征）；
- 当特征维度高时，可使用岭回归（Ridge） 或Lasso 回归（通过 L2/L1 正则化抑制过拟合）。