完全平方数(二)
解决方案
方法一:暴力枚举法 [超出时间限制]
这个问题要求我们找出由完全平方数组合成给定数字的最小个数。我们将问题重新表述成:
给定一个完全平方数列表和正整数 n,求出完全平方数组合成 n 的组合,要求组合中的解拥有完全平方数的最小个数。
注:可以重复使用列表中的完全平方数。
从上面对这个问题的叙述来看,它似乎是一个组合问题,对于这个问题,一个直观的解决方案是使用暴力枚举法,我们枚举所有可能的组合,并找到完全平方数的个数最小的一个。

我们可以用下面的公式来表述这个问题:
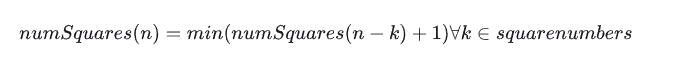
从上面的公式中,我们可以将其转换为递归解决方案。这里有一个例子。
算法:
Python 实现
class Solution(object):def numSquares(self, n):square_nums = [i**2 for i in range(1, int(math.sqrt(n))+1)]def minNumSquares(k):""" recursive solution """# bottom cases: find a square numberif k in square_nums:return 1min_num = float('inf')# Find the minimal value among all possible solutionsfor square in square_nums:if k < square:breaknew_num = minNumSquares(k-square) + 1min_num = min(min_num, new_num)return min_numreturn minNumSquares(n)上面的解决方案可以适用于较小的正整数 n。然而,会发现对于中等大小的数字(例如 55),我们也会很快遇到超出时间限制的问题。
简单的说,可能会由于过度递归,产生堆栈溢出。
