二叉树的拓展：平衡二叉树（定义，朴素c语言实现增删改查，平衡因子判断）通俗易懂

前情提要： 朴素c语言实现二叉树的概念和二叉搜索树（遍历，查找，删除，插入，更改）_c语言,删除二叉树(后序遍历)-CSDN博客

平衡二叉查找树（AVL）（平衡二叉树）定义

在二叉查找树中，有一种情况，就是当插入查找树的数据已经呈现一种有序的顺序，比如说一个已经排序好的数组array[10] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}，把这个数组中的元素依次插入到查找树中，就会造成一个现象，就是每插入的一个新的元素都在旧的元素的右边，这样一直插入下去，就给树插成一个链表了，这个树的效率就退化成O(n)了，为了避免这种情况，所以使用–平衡二叉查找树

参考文献：【平衡二叉树(AVL树)】 出错啦! - bilibili.com

平衡二叉查找树的特点就是所有结点的(左子树高度-右子树高度)的绝对值<=1，其中这个左子树高度-右子树高度就是平衡因子

下图就是一颗平衡二叉树

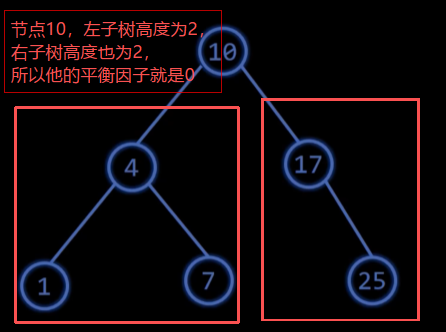
依次类推，节点17，左子树没有，所以左子树高度就是0，右子树高度为1，所以节点17平衡因子就是-1，

由此也可以看出，平衡因子只能是-1，0，1的才是平衡二叉树

平衡二叉树的增删改查和二叉搜索树是一样的，同样参考前文

朴素c语言实现二叉树的概念和二叉搜索树（遍历，查找，删除，插入，更改）_c语言,删除二叉树(后序遍历)-CSDN博客

只是每次插入或者删除某个节点以后，需要多一个判断是否失衡的过程，这个失衡的过程，称为旋转

旋转也分为左旋和右旋，左旋和右旋的方式和区别，会在下面的四种失衡情况种详细介绍

失衡的情况分为4种（图示）

1、LL

因为节点3的插入，导致二叉搜索树的根节点失衡了，平衡因子为2，且根节点的左子树根节点的平衡节点为1，

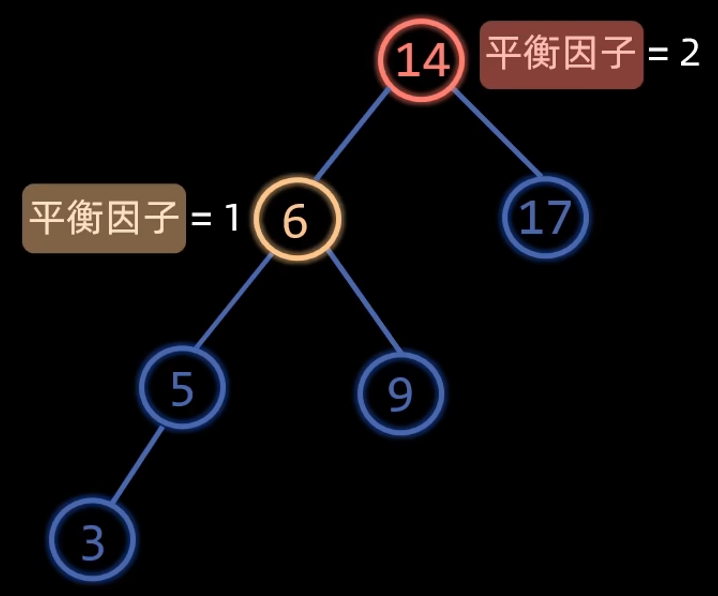
这种情况就是LL型失衡，需要右旋，下图就是右旋的过程

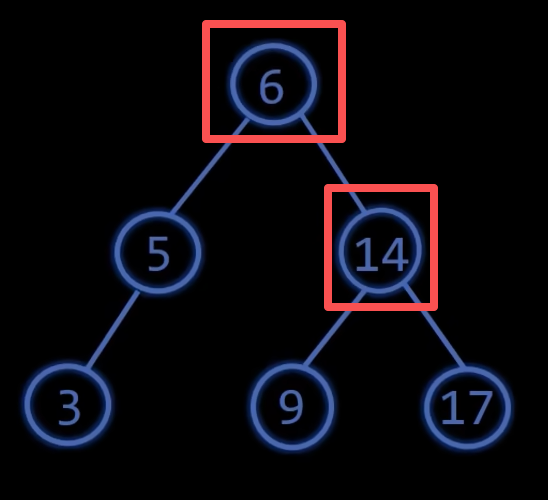
可以看到平衡因子为1的节点6变成了根节点，原来的根节点14变成了节点6的右子节点，节点6原来的右子节点9变成节点14的左节点，这就是网上常说的那句口诀：“冲突的右孩变左孩”。

2、RR

同理可知，因为节点17的插入，导致二叉搜索树根节点失衡了，平衡因子为-2，且根节点的右子树根节点的平衡节点为-1

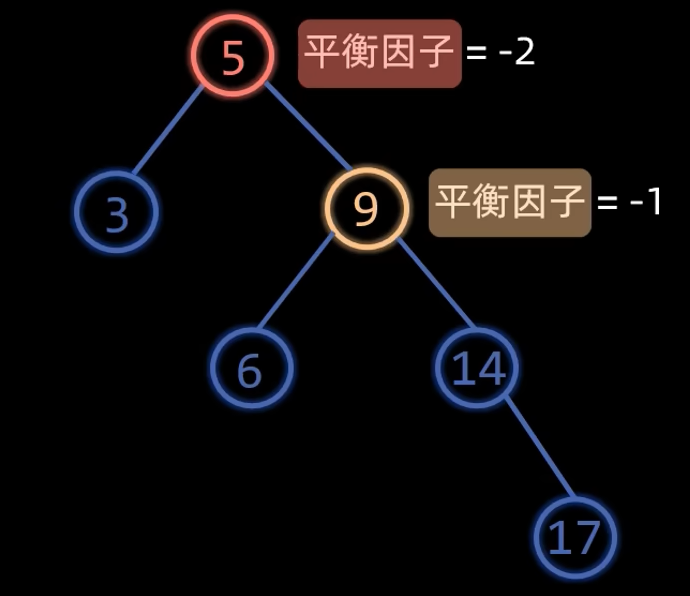
那就左旋，左旋原理跟右旋一样，口诀是：“冲突的左孩变右孩”；应该看的明白，不多赘述

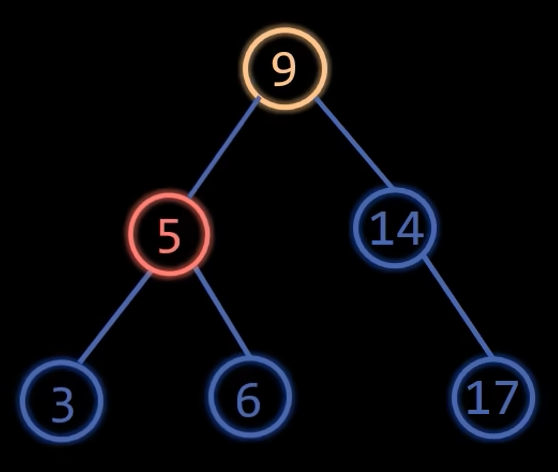
3、LR

LR型就是新插入的节点在左孩子的右子树上，导致根节点失衡了，根节点平衡因子为2，左孩子平衡因子为-1

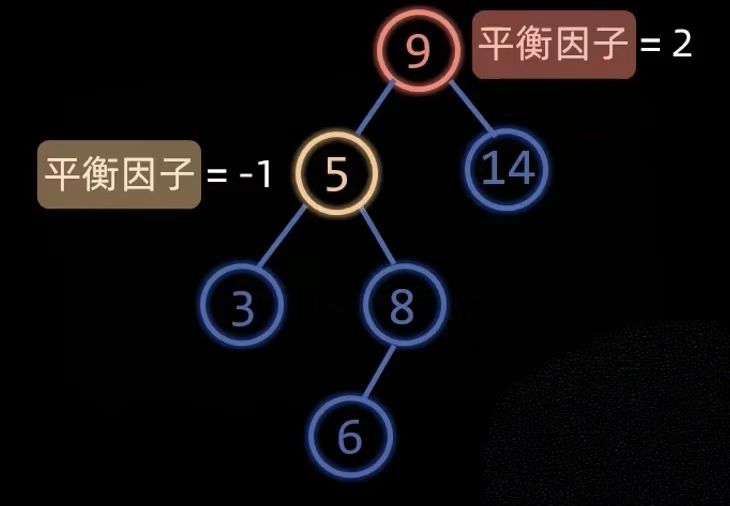
这种情况的话我们先左旋节点9的左孩子节点8，可以看到左旋节点8的过程也符合上文提到的左旋中：“冲突的左孩变右孩”相当于节点8左旋取代原本节点5的位置，然后节点5也左旋变成节点8的左孩子，原本节点8的左孩子就是口诀中提到的这个“冲突的左孩”。

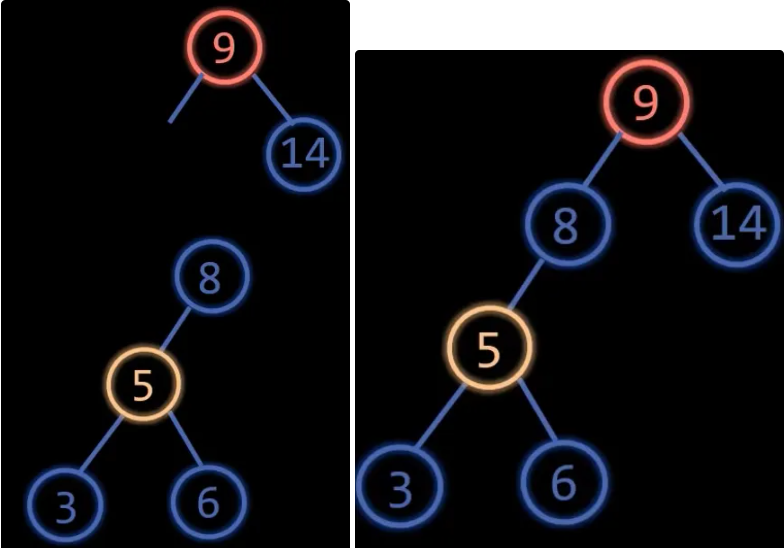
然后再右旋节点9，这一次的右旋没有冲突的节点

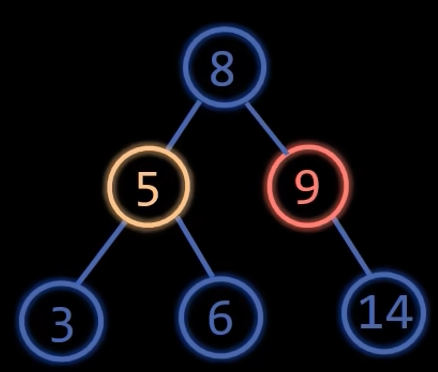
4、RL型

RL型就是新插入的节点在右孩子的左子树上，导致根节点失衡了，根节点平衡因子为-2，右孩子平衡因子为1

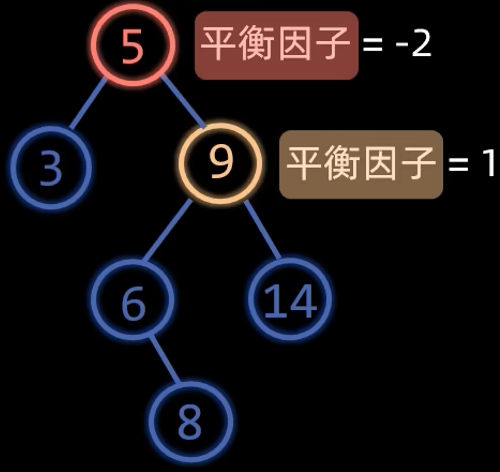
跟LR型原理一样，先右旋失衡节点的右孩子，然后再左旋失衡节点

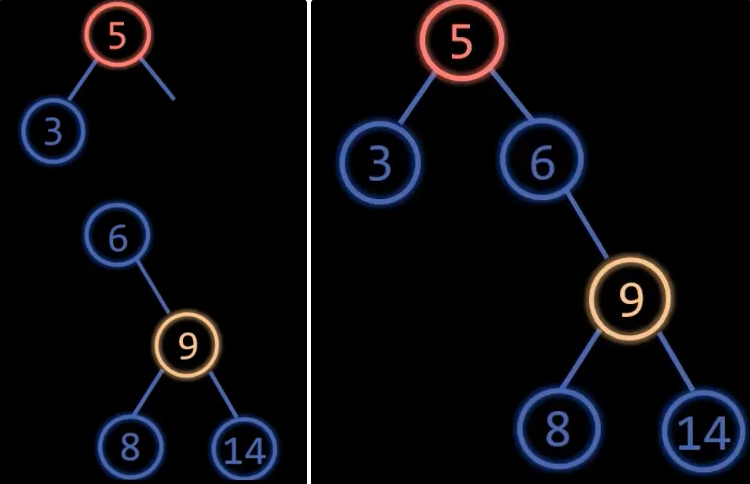
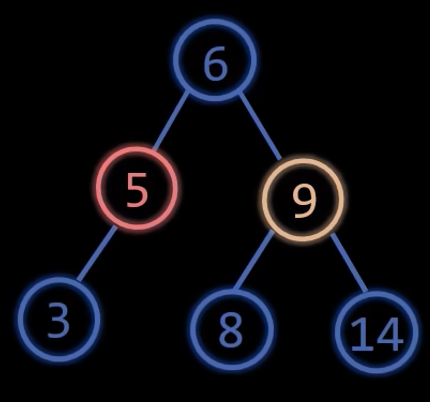
二叉平衡树的插入

由于节点9的插入，导致树出现了两个失衡节点，这个时候只需要调整距离插入节点9最近的失衡节点就可以了

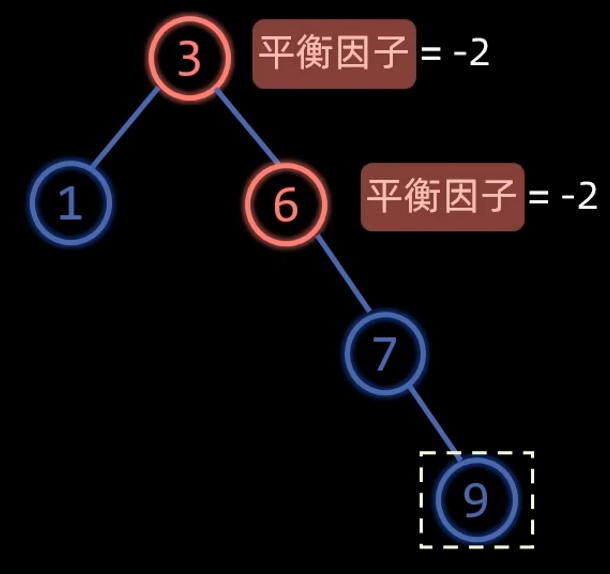
比如说直接左旋失衡节点6，然后就自动平衡了，所以当插入节点导致多个祖先节点失衡时，只需要调整距离插入节点最近的祖先节点即可

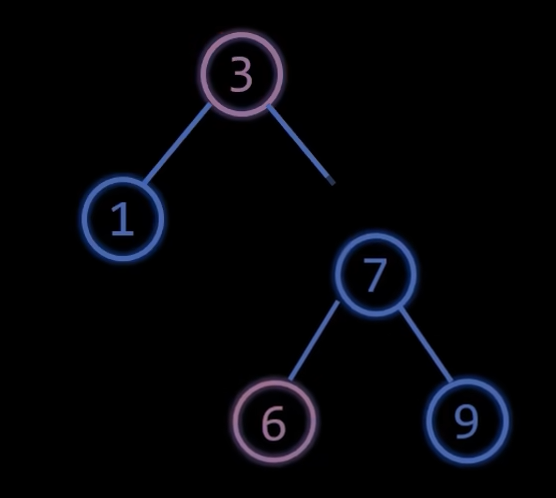
二叉平衡树的删除

删除的时候，跟插入不一样，插入的话只需要旋转距离插入节点最近的失衡节点即可，删除的话也需要先旋转距离插入节点最近的失衡节点，然后依次向上检查每一个祖先节点，因为，删除操作可能需要多次旋转祖先节点以保持平衡

代码实现：

请对照前情提要：二叉搜索树一起看

一、每一个节点需要维护的结构体，在搜索树的基础上增加了属性->高度

typedef struct AVLNode {int data;struct AVLNode* left;struct AVLNode* right;int height;  // 新增：高度
} AVLNode;

二、有关高度的辅助函数

有关高度的辅助函数分为以下三个，十分通俗易懂

// 获取高度
int getHeight(AVLNode* node) {return (node == NULL) ? 0 : node->height;
}// 更新高度
void updateHeight(AVLNode* node) {if (node != NULL) {node->height = 1 + (getHeight(node->left) > getHeight(node->right) ? getHeight(node->left) : getHeight(node->right));}
}// 获取平衡因子BF
int getBF(AVLNode* node) {return (node == NULL) ? 0 : getHeight(node->left) - getHeight(node->right);
}

三、两种旋转情况

1、右旋

    Z                   Y/ \                 / \Y   T4  ->         X   Z/ \                    / \
X   T3                 T3  T4

AVLNode* rightRotate(AVLNode* z) {AVLNode* y = z->left;AVLNode* t3 = y->right;y->right = z;z->left = t3;updateHeight(z);updateHeight(y);return y;
}

2、左旋

    Z                   Y/ \                 / \T1  Y    ->        Z   T4/ \             / \T2  T4          T1  T2

AVLNode* leftRotate(AVLNode* z) {AVLNode* y = z->right;AVLNode* t2 = y->left;y->left = z;z->right = t2;updateHeight(z);updateHeight(y);return y;
}

四、四种旋转情况：恢复平衡

1、LL

插入在左子树的左边。右旋根节点。

// bf是平衡因子
// LL的平衡因子判断条件
if (bf > 1 && data < node->left->data) {return rightRotate(node);
}

2、RR

插入在左子树的右边。先左旋左子树，再右旋根。

if (bf < -1 && data > node->right->data) {return leftRotate(node);
}

3、LR

插入在右子树的右边。左旋根节点。

if (bf > 1 && data > node->left->data) {node->left = leftRotate(node->left);return rightRotate(node);
}

4、RL

插入在右子树的左边。先右旋右子树，再左旋根。

if (bf < -1 && data < node->right->data) {node->right = rightRotate(node->right);return leftRotate(node);
}

五、AVL插入（增加平衡判断版）

AVLNode* insertAVL(AVLNode* node, int data) {if (node == NULL) {return createNode(data);  // 假设createNode现在用AVLNode}if (data < node->data) {node->left = insertAVL(node->left, data);} else if (data > node->data) {node->right = insertAVL(node->right, data);}updateHeight(node);int bf = getBF(node);// LLif (bf > 1 && data < node->left->data) {return rightRotate(node);}// RRif (bf < -1 && data > node->right->data) {return leftRotate(node);}// LRif (bf > 1 && data > node->left->data) {node->left = leftRotate(node->left);return rightRotate(node);}// RLif (bf < -1 && data < node->right->data) {node->right = rightRotate(node->right);return leftRotate(node);}return node;
}

六、AVL删除（增加平衡判断版）

// 先实现deleteNode类似朴素版，但用AVLNode，并返回节点
AVLNode* deleteAVL(AVLNode* root, int data) {// ... (类似deleteNode的核心逻辑，替换Node为AVLNode，并在替换后调用balance)// 假设核心删除后：updateHeight(root);int bf = getBF(root);// 类似insert的四种情况，但检查子树BF（因为删除可能影响多层）if (bf > 1 && getBF(root->left) >= 0) {  // LLreturn rightRotate(root);}if (bf > 1 && getBF(root->left) < 0) {   // LRroot->left = leftRotate(root->left);return rightRotate(root);}if (bf < -1 && getBF(root->right) <= 0) { // RRreturn leftRotate(root);}if (bf < -1 && getBF(root->right) > 0) {  // RLroot->right = rightRotate(root->right);return leftRotate(root);}return root;
}

总结

本篇文章的代码部分主要是以ai结合提示词辅助生成，所有的代码我全都review+编译过，实现过程十分简洁且清晰易懂，而且跟我上一篇写简单二叉树的博客的代码风格完美契合（我之前的文章代码都是手敲设计的，那时候的ai还远远不够先进），符合我的博客撰写通俗易懂的第一要义，也不经让我感叹现阶段ai功能的强大

特此鸣谢：molaGPT/Grok4 Fast

https://chatgpt.wljay.cn/v2/

这是ai回答生成的分享连接，点进去可以直接查看ai的回答，虽然有效期只有30天，不过在此留作纪念吧

Just a moment…

这是根据我之前的文章生成的提示词，虽然网站URL写错了，不过ai还是检索到了我的文章并生成了完美的回答