复变函数与积分变换 第三章——复变函数的积分

参考教程：

https://www.bilibili.com/video/BV1hV411v7KB?spm_id_from=333.788.videopod.episodes&vd_source=8f8a7bd7765d52551c498d7eaed8acd5

一、复变函数积分的概念

1、复变函数积分的定义

（1）有向曲线：

        设C为平面上给定的一条光滑（或按段光滑）曲线，如果选定C的两个可能方向中的一个作为正方向（或正向），那么就把C理解为带有方向的曲线，称其为有向曲线

        如果A到B作为曲线C的正向，那么B到A就是曲线C的负向，记为

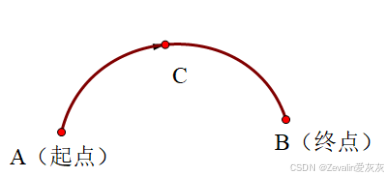
        关于曲线方向的说明：在今后的讨论中，常把两个端点中的一个作为起点，另一个作为终点，除特殊声明外，正方向总是指从起点到终点的方向

（2）简单闭曲线正向的定义：

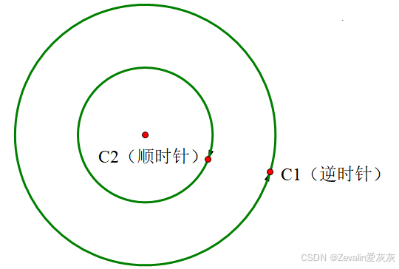
        简单闭曲线C的正向是指当曲线上的点P顺此方向前进时，邻近P点的曲线的内部始终位于P点的左方，与之相反的方向就是曲线的负方向

        如下图所示，曲线C1和曲线C2围成一个封闭区域，C1的逆时针方向为正向，C2的顺时针方向为正向

（3）积分的定义：

2、复变函数积分的性质

        复变函数积分与实变函数积分的定积分有类似的性质：

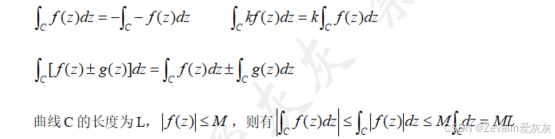
3、积分存在的条件及其计算方法

（1）积分存在的条件：

（2）积分的计算方法：

4、例题

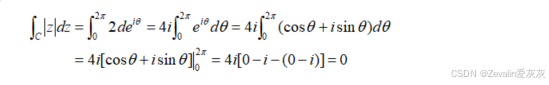
二、柯西-古萨定理

1、问题的提出

（1）对几个有象征性的复变函数做如下分析：

（2）由以上分析可得，积分值与积分路径是否无关，与被积函数是否解析、积分区域是否连通有关。

2、基本定理

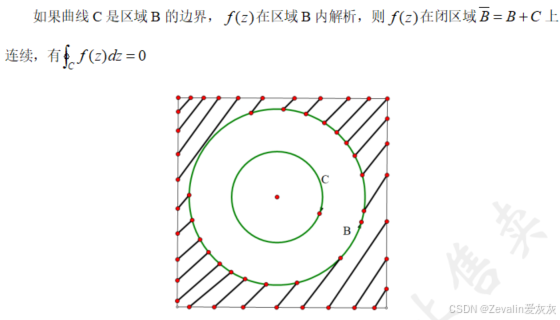
3、例题

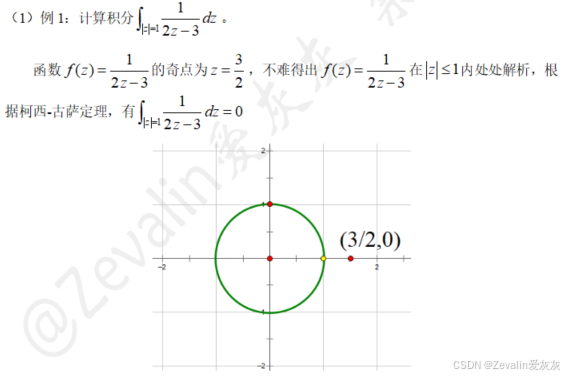
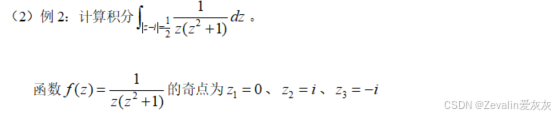
三、复合闭路定理

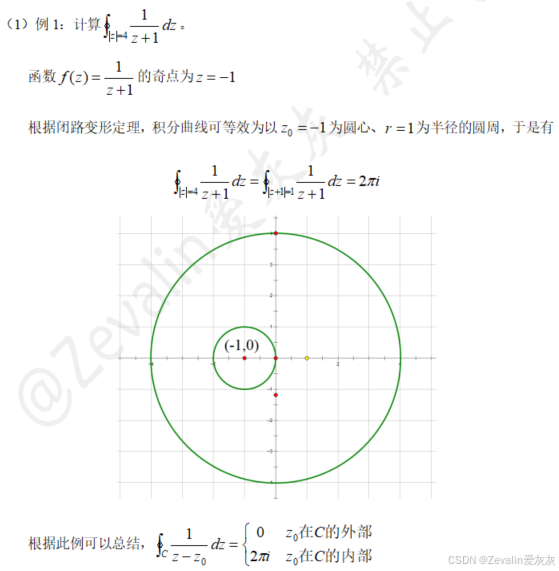
1、闭路变形原理

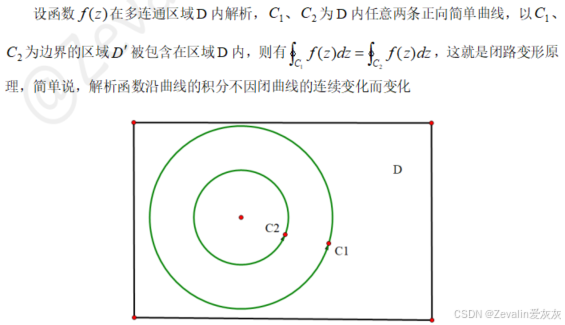
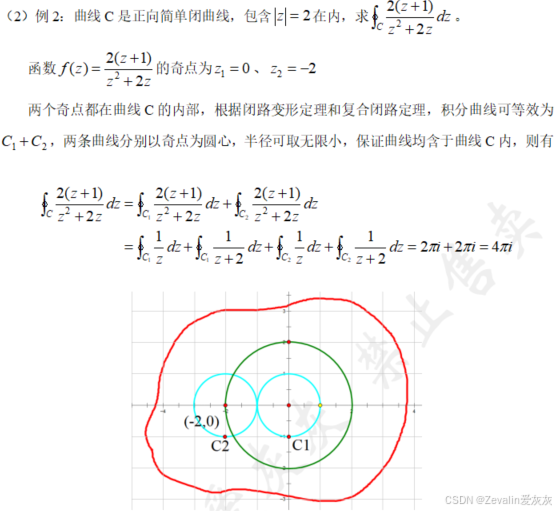
2、复合闭路定理

3、例题

四、原函数与不定积分

1、主要定理和定义

（1）定理1和定理2：

①定理1：

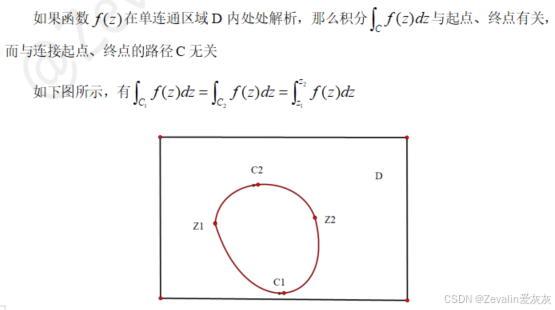
②定理2：

（2）原函数的定义：

（3）不定积分的定义：

（4）定理3：

2、例题

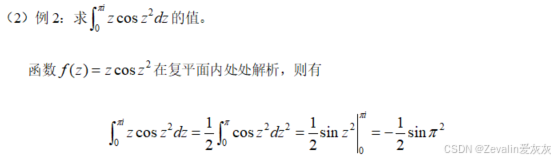
五、柯西积分定理

1、柯西积分公式

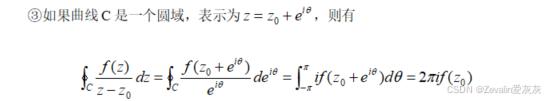
2、例题

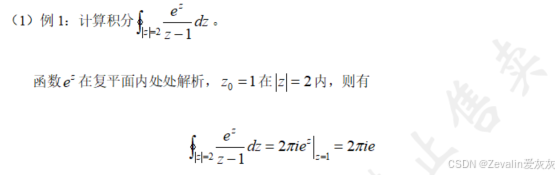
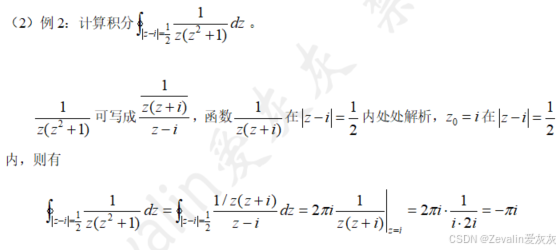
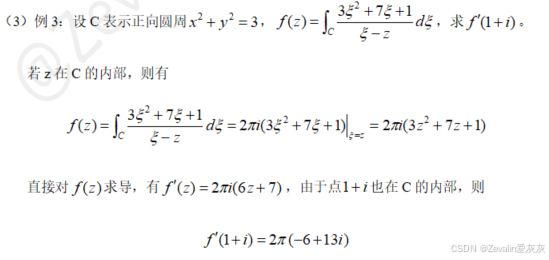
六、解析函数的高阶导数

1、主要定理

2、例题

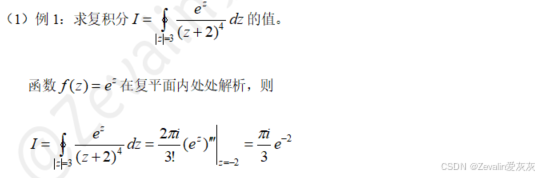
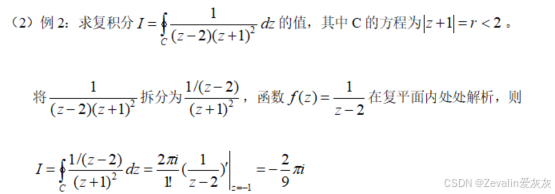
七、解析函数和调和函数的关系

1、调和函数的概念

2、解析函数与调和函数之间的关系

3、共轭调和函数

（1）共轭调和函数的定义：

（2）定理1：

（3）定理2：

（4）定理3：

4、例题