当前位置：首页 > news >正文

复杂系统中的机器学习瓦解与解体早期预警信号

news 2025/11/15 10:56:30

📌 论文基本信息

题目：Machine learning dismantling and early-warning signals of disintegration in complex systems
发表年份：2021年
作者：Marco Grassia, Manlio De Domenico, Giuseppe Mangioni
作者机构：
- 意大利卡塔尼亚大学
- 布鲁诺·凯斯勒基金会 CoMuNe 实验室
期刊：Nature Communications

🎯 研究目的

本研究旨在：

开发一种基于机器学习的网络瓦解方法，用于识别复杂网络中最关键节点，以最小代价实现系统瓦解；
提供一种早期预警指标，用于预测系统崩溃的风险；
超越传统启发式方法，通过数据驱动方式学习网络的高阶拓扑特征，提升瓦解效率与可解释性。

🛠️ 方法

基于机器学习的网络瓦解方法（GDM框架）。

该方法的核心思想是：不依赖人为设计的启发式规则，而是训练一个机器学习模型，让它从数据中自动学习“哪些节点对网络连通性至关重要”的复杂拓扑模式。

其具体方法可以分为以下几个关键步骤：

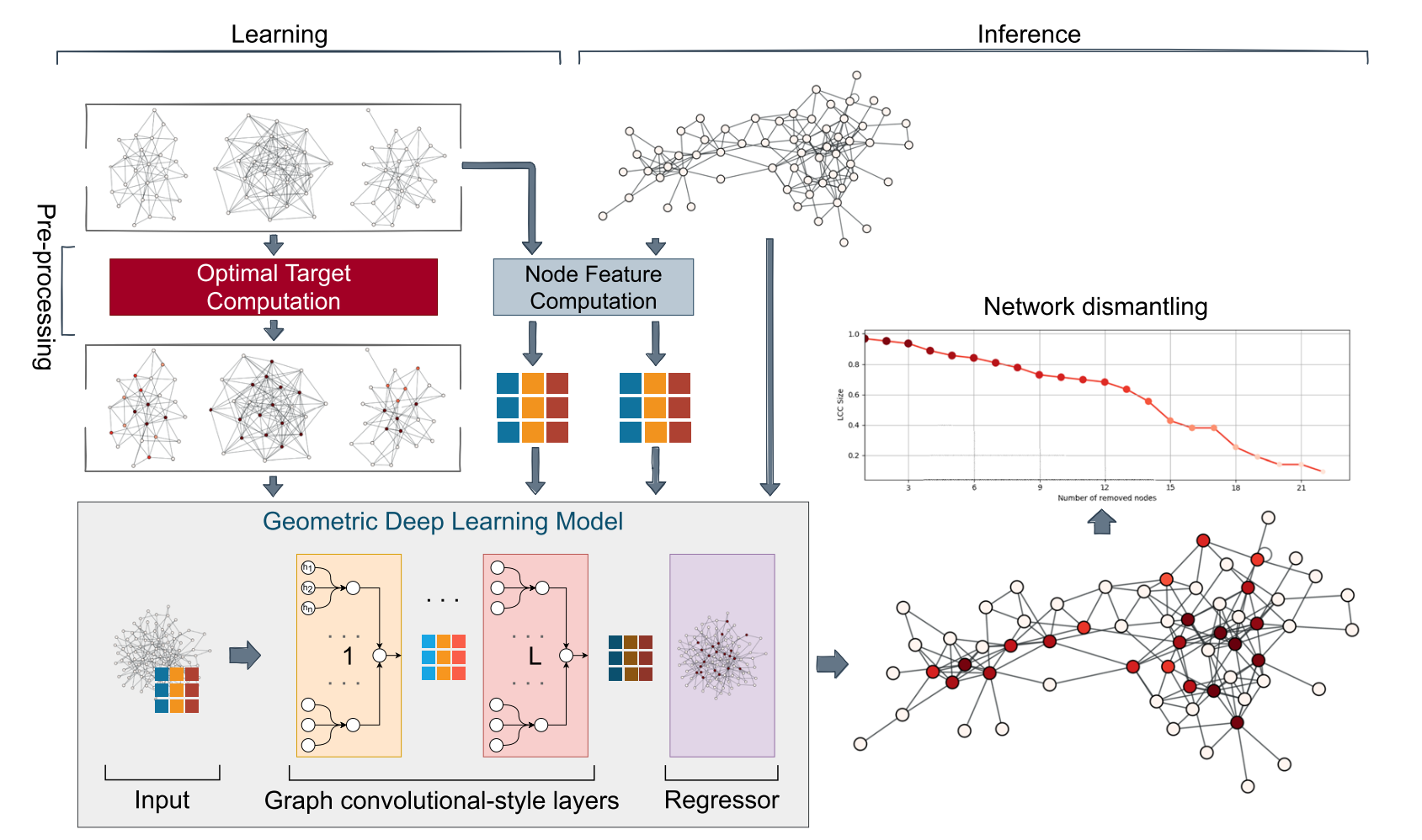
1. 训练数据生成：从小型合成网络中学习

由于大型网络的最优瓦解是NP难问题，无法直接获取标签，作者采用了一种“从小网络学习，向大网络推广”的策略。

网络生成：生成大量小型合成网络（例如25个节点），使用多种经典模型：
- Barabasi-Albert
- Erdős-Rényi
- 静态幂律模型
  这确保了训练数据的多样性，让模型能学习到不同拓扑结构（如均匀随机、无标度）的特征。
生成“真实标签”：对这些小网络，使用暴力搜索 方法找出所有能使其最大连通分量缩小到目标尺寸（如原大小的18%）的最小节点集合。这是可能做到的，因为网络很小。
节点标签分配：为每个节点分配一个介于0到1之间的“重要性”分数作为学习目标：
- 如果一个节点出现在所有最优瓦解集合中，其标签为 1。
- 如果只出现在一部分中，其标签为 0.5。
- 如果从未出现，其标签为 0。
  这样做是为了告诉模型，某些节点比其它节点更关键。

2. 机器学习模型：图注意力网络

模型的核心是一个图神经网络，具体是图注意力网络GAT。

输入：一个网络（图）及其节点的特征向量。
- 节点特征：作者使用了手工设计的特征，包括：
  - 局部特征：节点度数、度数的χ²值（衡量邻居度数的异质性）。
  - 二阶特征：局部聚类系数。
  - 全局特征：k-core值。
- 关键：这些特征是任意的，可以被替换或扩展为更复杂的特征。
模型架构：
- 图注意力层：这是模型的核心。它通过“注意力机制”聚合每个节点及其邻居的信息。这意味着模型不仅考虑邻居是谁，还学习为不同的邻居分配不同的重要性权重。通过堆叠多层GAT层，模型可以捕获节点多跳邻居之外的信息，从而理解网络的高阶拓扑结构。
- 残差连接：在每个GAT层后添加一个线性层，并将其输出与GAT层的输出相加，以稳定深层网络的训练。
- 回归器：最后是一个多层感知机，将GAT提取的高级节点特征映射为一个单一的标量值 p_n。
- 激活函数：使用Sigmoid函数，将 p_n 的值约束在 [0, 1] 区间内。
输出：对于网络中的每个节点 n，模型输出一个值 p_n，可以解释为该节点属于最优瓦解集合的概率。

3. 瓦解过程：静态攻击策略

排序：将目标网络的所有节点按其 p_n 值降序排列。这个排序列表就是模型的攻击序列。
攻击：按照这个序列，依次移除节点（如果该节点仍在最大连通分量中）。
静态性：这是该方法的一个关键特点。整个攻击序列是在瓦解过程开始前一次性计算好的。模型没有在移除节点后重新评估网络结构。这与许多传统方法（动态方法）形成对比，后者在每一步之后都会重新计算节点的重要性。

4. 早期预警信号

该方法的一个重要副产品是早期预警指标 Ω。预警指标 Ω 的设计步骤：

第一步：获取节点的“破坏概率”

这是整个方法的基础。使用训练好的 GDM 模型处理目标网络，为每个节点 n 计算出一个值 p_n。

p_n 的含义：模型认为节点 n 属于最优瓦解集合的概率。p_n 越高，意味着移除该节点对网络连通性的潜在破坏力就越大。

第二步：模拟瓦解并确定“致命一击”的节点集合

模拟攻击：按照 GDM 生成的攻击序列（即按 p_n 降序排列的节点列表），依次虚拟地移除节点。
确定临界点：在模拟过程中，监控最大连通分量的大小。找到那个导致网络发生渗流崩溃的临界点。通常，这定义为 LCC 大小突然急剧下降的时刻（例如，SLCC 出现峰值的时候）。
定义集合 S_0：将从第一个节点直到引发崩溃的那个临界点之前所移除的所有节点，定义为一个集合 S_0。这个集合包含了那些共同作用、将网络推向崩溃边缘的节点。

第三步：计算预警指标 `Ω`

预警指标 Ω 的计算公式非常简单：

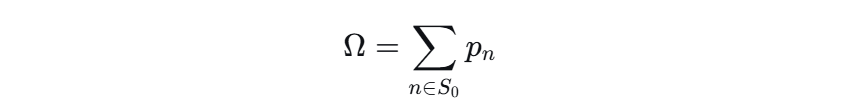
直观理解：

Ω 是导致系统崩溃所需的那一系列攻击的“总破坏概率”之和。
它回答了一个问题：“接下来要进行的这一系列关键攻击，其总体破坏力有多大？”

`Ω` 如何起到预警作用？

Ω 的值在 0 到 1 之间（理论上可以超过1，但意义类似），其动态变化提供了预警：

Ω 值较低时：

表示接下来要攻击的节点，其个体的破坏概率 p_n 都很低。
系统状态：即使移除很多节点，网络也可能只是缓慢退化，不会发生突然的崩溃。系统是安全的。

Ω 值升高并接近 1 时：

表示在未来的攻击序列中，包含了多个高价值目标。这些高 p_n 节点就像一颗颗“炸弹”，它们的连续爆炸将导致系统迅速解体。
系统状态：网络可能看起来还很大（LCC 下降不多），但实际上已经岌岌可危，处于崩溃的边缘。此时 Ω 发出了强烈的早期预警信号。

`Ω‘ 的变化率：

论文还提到了 Ω 的一阶导数 Ω’，它可以看作是 “攻击强度” 的实时指标。当 Ω‘ 出现尖峰时，意味着当前正在攻击一个极其关键的节点。

举例说明：为什么 `Ω` 比 LCC 更好？

想象一个由两个大型紧密团体，仅由少数几条桥梁连接而成的网络（如论文中的图7）。

攻击策略：使用GDM或基于介数的攻击，优先攻击这些桥梁。
LCC 的表现：
- 在移除前几座桥梁时，两个团体依然各自庞大，只是它们之间的连接断了。因此，LCC 的大小几乎保持不变（只是从100%降到略低于50%）。
- 直到最后一座关键桥梁被移除的瞬间，LCC 才会发生断崖式下跌。这时再预警为时已晚。
Ω 的表现：
- 在攻击序列中，这些桥梁节点都具有很高的 p_n 值。
- 因此，当这些桥梁节点陆续进入集合 S_0 时，Ω 值会快速累积并攀升。
- 在最后一座桥梁被移除之前，Ω 可能就已经达到了 0.8 或 0.9，发出了明确的红色警报，而此时 LCC 看起来还很大。

✅ 训练与测试过程

一、训练数据：用于“教会”模型

训练数据全部是人工生成的、小型的合成网络。

来源：计算机生成。
规模：每个网络仅包含 25个节点。这个大小确保了可以通过暴力搜索找到最优解。
生成模型：使用了三种经典的网络生成模型，以确保训练数据的多样性：
1. Barabasi-Albert模型：生成具有无标度特性（存在枢纽节点）的网络。
2. Erdős-Rényi模型：生成随机连接的均匀网络。
3. 静态幂律模型：另一种生成具有幂律度分布网络的方法。
标签：对每个小网络，使用暴力搜索 找出所有可能的最小瓦解集合，并为每个节点计算一个 0到1之间的“重要性”分数（基于它出现在最优集合中的频率）。这个分数就是模型学习的目标。

总结：模型是在小型、多样化的合成网络上，通过学习最优瓦解的精确解来接受训练的。

二、测试与验证数据：用于评估模型性能

为了检验训练好的模型是否有效，作者在两大类数据上进行了广泛的测试：

1. 真实世界网络

这是检验模型泛化能力的核心。作者在 50多个 来自不同领域的真实网络数据集上进行了测试，涵盖了：

社交网络：如 advogato, ego-twitter, slashdot-threads（用户关系网络）
基础设施网络：如 eu-powergrid（欧洲电网）, internet-topology（互联网拓扑）, opsahl-openflights（航空网络）
生物网络：如 dimacs10-celegansneural（线虫神经网络）, foodweb-baydry（食物网）
信息/技术网络：如 web-EPA（网页链接网络）, p2p-Gnutella（文件共享网络）, linux（软件依赖网络）
合作/引用网络：如 dbip-cite（引用网络）, wikipedia_link_kn（维基百科链接网络）
交通网络：如 moreno_train（火车网络）
经济与犯罪网络：如 corruption（巴西腐败网络）, econ-wm1（经济网络）