双种群自适应差分进化算法 L-NTADE

Dual-Population Adaptive Differential Evolution Algorithm L-NTADE

摘要（Abstract）

差分进化（DE）是一种高效且流行的启发式优化方法。然而，像大多数进化算法一样，它的性能对其参数设置很敏感。近年来，许多研究致力于为DE开发参数自适应技术，其中大多数研究都基于使用单个种群和贪婪选择策略的经典算法框架。在本研究中，我们提出了一种新颖的双种群DE算法，称为L-NTADE（采用线性种群规模缩减的新解与顶部解自适应差分进化）。该算法受到无界差分进化（UDE）思想的启发，但与之不同，它使用两个大小受限的种群：一个称为“新解”种群，持续用新生成的解进行更新；另一个称为“顶部解”种群，保留在整个搜索过程中找到的最佳解。我们为所提出的算法考虑了不同的变异策略，这些策略以特定方式利用两个种群中的个体。L-NTADE采用了来自现代DE变体（如SHADE）的参数自适应技术，并引入了线性种群规模缩减（LPSR）机制。所提出的方法在CEC 2017和CEC 2022单目标边界约束数值优化基准测试集上进行了测试。实验结果表明，L-NTADE在求解复杂多模态问题时表现出色，并且与当前最先进的算法相比具有竞争力。此外，我们还对算法行为进行了分析，揭示了两个种群在搜索过程中的不同角色。

关键词： 差分进化；参数控制；自适应；双种群；全局优化

---

1. 引言（Introduction）

当前，进化算法（EA）领域正与计算智能（CI）的其他方法，如神经网络（NN）和模糊逻辑系统（FL），一同快速发展。在EA和群体智能（SI）框架内提出的启发式优化方法，旨在找到能够解决复杂全局优化问题的最佳算法方案[1]。针对约束优化、多目标优化、超多目标优化、布尔优化、整数优化和双层优化等特定问题，已经开发了相应的算法版本[2]。然而，针对单目标数值问题提出的算法通常作为其他研究方向的基础，并常被用于解决复杂的工程问题[3,4]。

近年来，差分进化（DE）[5] 吸引了众多研究人员的关注，因为与其他EA和群体智能方法（如遗传算法（GA）[6]、进化策略（ES）[7]、粒子群优化（PSO）[8] 以及许多其他方法[9,10]）不同，它具有高效性和实现简单性的特点。这在近期优化竞赛（如IEEE进化计算大会（CEC））的参与情况中得到了体现，其中提交的大多数算法和获胜者都是基于DE的方法[11]。

关于差分进化的研究主要集中于参数自适应问题，因为已知DE对三个主要参数（即缩放因子、交叉率和种群大小）高度敏感[12,13]。各种自适应方案被提出，从SaDE [14] 算法开始，其中缩放因子采用正态分布采样，而交叉率则基于经验学习。其他方法，如[15,16,17]，使用了预定义的参数值池。一种相对简单的参数值随机化方法已被证明表现良好，正如jDE [18] 所展示的那样，随后出现了类似的方法。随着使用记忆单元存储成功参数值的JADE算法[19]的发展，出现了最流行的SHADE [20] 以及采用种群规模缩减的L-SHADE [21]，还有许多其他算法，例如[22]。近期关于差分进化的研究催生了许多方法，例如TVDE（具有时变策略）[23]、CSDE（具有组合变异策略）[24]、qIDE（具有基于Q学习的参数调整策略）[25]、MPPCEDE（具有多种群和多策略）[26] 和RL-HPSDE（基于强化学习的自适应）[27]。也有研究尝试使用遗传编程[28]和神经进化[29]来实现DE参数自适应的自动设计。

然而，DE的主要算法框架仍然保持不变。在大多数研究中，它拥有单个种群和一个可选的外部存档，并且仅当后代优于父代时才进行替换。在一些研究中，研究者尝试偏离主流方案，例如在HARD-DE [30]中引入了分层存档，在j21 [31]中引入了大小种群，在类DE的ACSK [32]中引入了初级和高级个体，以及在GRDE [33]中引入了全局替换。最近，文献[34]提出了无界DE（UDE），其中种群可以无限增长，并应用特定的选择机制来驱动搜索。

在本研究中，我们进一步发展了UDE的思想，提出了一种双种群DE算法，第一个种群称为新解种群（new），第二个种群称为顶级种群（top）。新解种群具有特定的更新规则，保留最近发现的优良解，而顶级种群则保留在整个搜索过程中找到的最佳解。由此产生的L-NTADE算法（采用线性种群规模缩减的新解与顶部解自适应差分进化）考虑了具有多种变异策略的若干种改进版本。该算法在CEC 2017 [35] 和 CEC 2022 [36] 基准测试集上进行了测试，并在部分测试函数上展现了高效率和特定优势。本研究的主要特点可概括如下：

1. 采用新版current-to-pbest变异策略的新型双种群差分进化方案，其策略将顶级种群个体作为前p%最佳个体之一使用，性能优于其他策略；
2. 与新解种群配套的新选择（替换）规则，与使用经典选择的情况相比，显著提高了算法性能；
3. 所提出的L-NTADE算法在复杂的多模态测试问题上表现更好。

第2节包含相关工作概述，第3节描述了所提出的方法，第4节包含实验设置和结果，随后对结果进行了讨论，第5节对论文进行了总结。

---

2. 相关工作（Related Work）

2.1 差分进化（Differential Evolution）

差分进化（Differential Evolution）是一种流行的启发式数值优化方法，由 Storn 和 Price 最初提出 [37]。DE 是一种基于种群的方法，因此它首先在搜索范围内随机初始化一组 N 个个体 $x_i=(x_{i,1},x_{i,2},\dots ,x_{i,D})$，$i=1,\dots ,N$：

S={xi∈RD∣xi=(xi,1,xi,2,…,xi,D):xij∈[xlbj,xubj]}(1)S=\{x_{i}\in R^{D}|x_{i}=(x_{i,1},x_{i,2},\ldots,x_{i,D}):x_{ij}\in[x_{lbj},x_{ ubj}]\} \tag{1}S={xi​∈RD∣xi​=(xi,1​,xi,2​,…,xi,D​):xij​∈[xlbj​,xubj​]}(1)

其中 $j=1,\dots ,D$，$D$ 是搜索空间的维度。每个个体使用均匀分布生成：

$$x_{ij}=x_{lbj}+rand\times (x_{ubj}-x_{lbj}).\text{\hspace{1em}(2)}$$

尽管 DE 最初是为数值单目标无约束问题提出的，但它可以通过修改用于其他类型的问题 [12]。DE 的主要特点在于其基于差分的变异算子，这是搜索过程的关键组成部分。存在几种变异策略的变体，包括 rand/1、rand/2、best/1、best/2、current-to-best/1 和 current-to-pbest/1 [13]。原始版本 rand/1 生成新解的方式如下：

$$v_{ij}=x_{r1,j}+F\times (x_{r2,j}-x_{r3,j}),\text{\hspace{1em}(3)}$$

其中 $v_i$ 被称为变异向量或供体向量，$x_{i,j}$ 是第 $i$ 个候选解的第 $j$ 个坐标，索引 $i$、$r1$、$r2$ 和 $r3$ 都互不相同，$F$ 是从 $[0,2]$ 中选择的缩放因子。缩放因子参数是 DE 最重要的参数之一，因为已证明算法对其值高度敏感 [5]。

变异之后，执行交叉步骤，该步骤将生成的供体向量和在变异中作为基线的目标向量（即种群中的第 $i$ 个个体）进行组合。生成的试验向量 $u_i$ 通常使用二项式交叉算子生成：

$$u_{i,j}=\{\begin{array}{ll}{v}_{i,j},& \text{if }rand(0,1)<Cr\text{ or }j=jrand\\ x_{i,j},& \text{otherwise}\end{array}.\text{\hspace{1em}(4)}$$

在这个公式中，$Cr\in [0,1]$ 是交叉率，$jrand$ 是从 $[1,D]$ 中随机选择的索引。需要 $jrand$ 索引是为了确保至少有一个分量是从供体向量继承的。否则，评估一个个体的副本将是计算资源的浪费。最近的一项研究表明，尽管有此修正，DE 中仍可能出现重复个体的问题 [38]。

应用变异算子可能会导致解超出搜索空间的边界。因此，应在 DE 中应用特定的边界约束处理方法（BCHM）。特别地，一种流行的方法称为中点目标法（midpoint-target），其中第 $i$ ($i=1,\dots ,N$) 个向量的第 $j$ ($j=1,\dots ,D$) 个坐标通过以下方式被限制在区间 $[x_{lb,j},x_{ub,j}]$ 内：

$$u_{i,j}=\{\begin{array}{ll}\frac{x_{lb,j}+x_{i,j}}{2},& \text{if }{v}_{i,j}<x_{lb,j}\\ \frac{x_{ub,j}+x_{i,j}}{2},& \text{if }{v}_{i,j}>x_{ub,j}\end{array}.\text{\hspace{1em}(5)}$$

这里，如果变异向量的第 $j$ 个分量大于对应区间 $[x_{lb,j},x_{ub,j}]$ 的上界或小于其下界，则使用其父向量 $x_i$ 来设置该分量的新值。请注意，此步骤可以在变异之后或交叉之后应用。

经典 DE 框架中的最后一步称为选择（selection），但与遗传算法中的选择不同，它扮演着替换算子（replacement operator） 的角色。如果新生成的试验向量 $u_i$ 优于对应的目标向量，则发生替换：

$$x_i=\{\begin{array}{ll}{u}_i,& \text{if }f(u_i)\le f(x_i)\\ x_i,& \text{if }f(u_i)>f(x_i)\end{array}.\text{\hspace{1em}(6)}$$

尽管已知这种选择机制简单有效，但已有一些尝试改进它，例如利用邻域信息 [39]。

2.2 DE 的改进（DE Modifications）

由于 DE 变体在进化计算中的高度普及和大量研究，在此对所有现有方法进行全面综述是不切实际的。因此，建议感兴趣的读者参阅诸如 [12, 13, 40] 的综述，关于特定类型 DE 的专门研究，例如 [22]，或关于算子 [41] 的研究，以及我们之前关于选择压力 [42] 和参数自适应 [43] 的一些研究。尽管如此，这里我们将重点关注一些与当前工作特别相关的研究。

DE 发展的一个重要里程碑是 Zhang 和 Sanderson [44] 提出的 JADE 算法。JADE 引入了最高效的变异策略之一current-to-pbest/1，该策略至今仍在大多数 DE 变体中使用，其描述如下：

$$v_{ij}=x_{ij}+F\times (x_{pbestj}-x_{ij})+F\times (x_{r1j}-x_{r2j}),\text{\hspace{1em}(7)}$$

其中 pbest 是前 $pb\ast 100\%$ 最佳个体中不同于 $i$、$r1$ 和 $r2$ 的某个个体的索引。包含差值的两个括号实现了两个主要特征：通过朝向最佳解之一移动来进行开发（exploitation），以及通过添加两个随机选择的解之间的差分向量来进行探索（exploration）。此外，将 $F$ 增加到 1 意味着生成的解更接近最佳解，同时用第二个差分向量迈出更大的步长，而较小的 $F$ 值意味着在目标向量附近进行探索。JADE 还引入了外部存档（external archive） $A$ 的概念，这是一个在选择过程中被更优解替换掉的解的集合。存档中的解在 current-to-pbest/1 中被用来替代最后一个向量 $x_{r2}$。存档被证明对于提高搜索效率至关重要，并且存档处理技术是一个重要的研究领域 [30, 45]。

JADE 的效率启发了其他研究人员开发其改进版本。特别地，Tanabe 和 Fukunaga [20] 提出的 SHADE 算法通过引入一组 $H$ 个记忆单元 $(M_{F,h},M_{Cr,h})$ 改进了 JADE 的参数自适应，每个单元包含一对 $F$ 和 $Cr$ 值。对于每个变异和交叉算子，参数值按如下方式采样：

$$\{\begin{array}{l}F=randc(M_{F,k},0.1)\\ Cr=randn(M_{Cr,k},0.1)\end{array}.\text{\hspace{1em}(8)}$$

这里，$randc$ 是柯西分布随机值，$randn$ 是正态分布随机数，$k$ 为每个个体从 $[1,H]$ 中选择。如果生成的 $Cr$ 值超出 $[0,1]$ 范围，则将其截断至此范围。如果 $F$ 大于 1，则将其设为 1；如果 $F$ 小于 0，则重新生成直到其为正。在每一代结束时，使用成功的 $F$ 和 $Cr$ 值更新索引为 $h$（每代从 1 迭代到 $H$）的记忆单元。成功的参数值是指那些在适应度方面带来改进的值，即，如果一个后代替换了父代，则 $F$ 和 $Cr$ 被存储在 $S_F$ 和 $S_{Cr}$ 数组中，改进值 $\Delta f=|f(u_j)-f(x_j)|$ 被存储在 $S_{\Delta f}$ 中。记忆单元的更新首先通过计算加权 Lehmer 均值 [46] 来执行：

$$mea{n}_{wL}=\frac{{\sum }_{j=1}^{|S|}{w}_j{S}_j^2}{{\sum }_{j=1}^{|S|}{w}_j{S}_j},\text{\hspace{1em}(9)}$$

其中 $w_j=\frac{S_{\Delta f_j}}{{\sum }_{k=1}^{|S|}{S}_{\Delta f_k}}$，$S$ 是 $S_{Cr}$ 或 $S_F$。

记忆单元中的值更新如下：

$$\{\begin{array}{l}{M}_{F,k}^{t+1}=0.5(M_{F,k}^t+mea{n}_{(wL,F)})\\ M_{Cr,k}^{t+1}=0.5(M_{Cr,k}^t+mea{n}_{(wL,Cr)})\end{array},\text{\hspace{1em}(10)}$$

其中 $t$ 是当前迭代次数。

在 [43] 中，提出了有偏参数自适应，通过引入一个附加参数 $pm$ 来修改 Lehmer 均值：

$$mea{n}_{wL}=\frac{{\sum }_{j=1}^{|S|}{w}_j{S}_I^{pm}}{{\sum }_{j=1}^{|S|}{w}_j{S}_j^{pm-1}}.\text{\hspace{1em}(11)}$$

这个附加参数允许 $F$ 或 $Cr$ 的自适应偏向更小或更大的值。L-SHADE 中的标准设置是 $pm=2$，而在 [43] 中表明，增加该值并生成更大的 F 可能会在高维问题中带来更好的结果。

SHADE 的另一个重要改进是 L-SHADE [21]，它引入了一种简单的种群大小控制策略，称为线性种群大小缩减（LPSR）。该算法开始时种群中有 $N{P}_{max}$ 个个体，并逐渐将其数量减少到 $N{P}_{min}$ 个个体：

$$N{P}_{g+1}=round\left(\frac{N{P}_{min}-N{P}_{max}}{NF{E}_{max}}NFE\right)+N{P}_{max},\text{\hspace{1em}(12)}$$

其中 $N{P}_{min}=4$，$NFE$ 和 $NF{E}_{max}$ 分别是当前和总的可用函数评估次数。在每一代结束时，如果需要，从种群中移除最差的解，并且存档大小也会减小。最近的一些研究提出了使用正交设计初始化非常大种群的 L-SHADE 变体 [47]。

在 [42] 中，研究了选择压力对 DE 性能的影响，结果表明添加锦标赛或基于排名的选择策略可能是有益的。指数基于排名的选择是通过根据个体在排序数组中的适应度来选择个体实现的，分配的排名如下：

$$ran{k}_i=e^{-kp\cdot \frac{i}{NP}},\text{\hspace{1em}(13)}$$

其中 $kp$ 是控制压力的参数，$i$ 是个体编号。较大的排名分配给较好的个体，并使用离散分布进行选择。

L-SHADE 算法的重要性通过为其提出的修改数量得到了证明。例如，jSO [48] 提出了一种改进的变异策略和根据搜索阶段调整的特定参数自适应规则；L-SHADE-RSP [49] 引入了基于排名的选择压力；LSHADE-SPACMA [50] 使用了与 CMA-ES 的混合；NL-SHADE-RSP [51] 提出了非线性种群大小缩减、交叉率排序和自适应存档使用；MLS-LSHADE [52] 增加了多起点局部搜索；DB-LSHADE 提出了基于距离的参数自适应 [53]。尽管所有这些研究都展示了现代 DE 方法的不同可能性，但根据最近一项关于无界 DE [34] 的研究，“具有被新生成个体替换的个体的种群概念是差分进化中一个普遍存在的思想”。在下一节中，将提出一个偏离这一概念的算法框架。

---

3. 提出的方法（Proposed Approach）

受到无界种群（UDE）实验的启发，并得到该设置下若干初步测试的支持，我们提出了 L-NTADE 算法。L-NTADE 维护两个种群，第一个称为新解种群，第二个称为顶级种群。与 UDE 不同，两个种群的规模都是受限的，因为初步测试表明，处理非常大的种群需要巨大的计算量。

L-NTADE 算法首先初始化一个包含 $N_{max}$ 个个体 $x_i^{new}$ ($i=1,\dots ,N_{max}$) 的种群。之后，该种群中的个体会被复制到顶级种群 $x^{top}$ 中。

L-NTADE 使用了 SHADE 算法中 current-to-pbest 变异策略的变体和参数自适应技术，但没有使用外部存档。本研究中考虑的变异策略如下：

1. r-new-to-ptop/t/t: $$v_{i,j}=x_{r1,j}^{new}+F\times (x_{pbest,j}^{top}-x_{i,j}^{new})+F\times (x_{r2,j}^{top}-x_{r3,j}^{top})$$
2. r-new-to-ptop/t/n: $$v_{i,j}=x_{r1,j}^{new}+F\times (x_{pbest,j}^{top}-x_{i,j}^{new})+F\times (x_{r2,j}^{top}-x_{r3,j}^{new})$$
3. r-new-to-ptop/n/t: $$v_{i,j}=x_{r1,j}^{new}+F\times (x_{pbest,j}^{top}-x_{i,j}^{new})+F\times (x_{r2,j}^{new}-x_{r3,j}^{top})$$
4. r-new-to-ptop/n/n: $$v_{i,j}=x_{r1,j}^{new}+F\times (x_{pbest,j}^{top}-x_{i,j}^{new})+F\times (x_{r2,j}^{new}-x_{r3,j}^{new})$$

此处使用了以下符号表示：术语 r-new 和 r-top 分别表示从新解种群或顶级种群中选择一个随机个体作为目标解；p-new 和 p-top 表示从新解种群或顶级种群的前 pb% 最佳个体中选择一个；而 /t 或 /n 表示在第二个差分向量中使用来自顶级种群或新解种群的个体。请注意，目标向量并非像大多数 DE 中那样是第 i 个向量，而是从某个种群中随机选择的向量。选择这些变异策略是因为它们代表了应用不同种群个体的不同场景，其中后两种变体是极端情况（仅使用其中一个种群），其他是中间情况。这里可能的组合数量很多，我们只考虑了那些效率水平尚不明确的情况。此外，由于索引来自不同种群，仅当索引来自同一种群时才需要检查它们是否相等。

pb 参数的控制方式如下：在搜索开始时，$pb$ 被设置为 $p{b}_{max}$，然后线性降低至 $p{b}_{min}$：

$$p{b}_{g+1}=round\left(\frac{p{b}_{min}-p{b}_{max}}{NF{E}_{max}}NFE\right)+p{b}_{max}\text{\hspace{1em}(14)}$$

其中 $g$ 是当前代数，为简洁起见下文将省略。此外，如果可供选择的最佳个体数量少于 2，则将其设置为 2。在搜索过程中线性减小 pb 会导致在搜索接近结束时贪婪度增加。

L-NTADE 中的交叉步骤保持不变，即像 L-SHADE 算法一样，使用经典二项式交叉生成 $u_i$。所使用的边界约束处理方法是前文提到的中点目标法。

然而，选择步骤是 L-NTADE 算法的主要特点之一。这里的主要思想是通过维护两个种群来模拟无界种群的行为，从中选择最新和最佳的个体。选择步骤取决于变异策略，特别是目标解是从顶级种群还是新解种群中选择的。更新的主要思想仍然相同：如果试验向量优于目标向量，则应保存它。然而，新解总是被保存到新解种群中。在每次成功生成解之后，用于存放试验向量的个体索引 $nc$ 从 1 迭代到 $N_{cur}$，并在达到 $N_{cur}$ 时重置为 1。选择步骤可以描述如下：

$$x_{nc}=\{\begin{array}{ll}{u}_i,& \text{if }f(u_i)\le f(x_{r1}^{t|n})\\ x_{nc},& \text{if }f(u_i)>f(x_{r1}^{t|n})\end{array}.\text{\hspace{1em}(15)}$$

这里，$t|n$ 表示根据所使用的变异策略，目标向量可以从顶级种群或新解种群中选择。成功的试验向量会立即被复制到当前的新解种群中，并且由于变异时随机选择解，它们可以在同一代中用于生成其他向量。尽管选择前 pb% 最佳个体索引的操作每代只执行一次，但我们认为在每次成功选择后进行排序和寻找最佳解的意义不大。此外，这可能只对第 5 种变异策略变体构成问题。所有成功的解都会额外存储在一个临时池 $x^{temp}$ 中，并且在代结束时，将 $x^{top}$ 和 $x^{temp}$ 合并、排序，并且只将前 $N_{cur}$ 个个体保存到 $x^{top}$ 中，其中 $N_{cur}$ 是两个种群的当前大小。通过这种方式，顶级种群始终包含整个搜索过程中找到的前 $N_{cur}$ 个最佳个体。

种群大小控制策略与 L-SHADE 相同，唯一的区别是新解种群和顶级种群的大小都在线性减小，并且具有相同的初始和最终大小。以下方程对两个种群都适用，使用 $N_{max}$ 和 $N_{min}$：

$$N_{cur}^g=round\left(\frac{N_{min}-N_{max}}{NF{E}_{max}}NFE\right)+N_{max}\text{\hspace{1em}(16)}$$

L-NTADE算法的伪代码如算法1所示。

该算法需要目标函数、问题维度、总计算资源和初始种群大小才能运行，并返回最佳解及其值，如算法 1 的前两行所示。在此之后，主要参数在第 3 行和第 4 行设置。第 5 行描述了初始化步骤，其中新解种群填充了随机个体。在第 6 行，新解种群及其目标函数值被复制到顶级种群。接着，开始主循环，在每代开始时（第 8 行），成功的 $F$、$Cr$ 和 $\Delta f$ 值集合被清空。在第 9 行，根据适应度值对新解种群中的个体进行排序，并为个体分配排名。此后，在第 10 行开始对个体进行循环。由于变异策略需要随机索引，因此在第 11 行生成第一个索引。接着，在第 12 行随机选择当前记忆索引，该索引用于分别在第 13-14 行和第 15-18 行生成 $Cr$ 和 $F$ 值。在第 19-23 行，生成变异所需的其余索引，直到它们互不相同。在第 21 行，$r2$ 索引可以根据所使用的变异策略随机生成，或使用第 9 行计算的排名来生成。第 24、25 和 26 行实现了 DE 的主要搜索算子，例如变异和交叉，以及边界约束处理方法。

在此之后，一旦试验向量生成，就在第 27 行计算其适应度值。在第 28–35 行，执行选择操作，即如果试验向量优于具有索引 r1 的随机选择个体，则将其保存在临时种群中，并且当前的 F 和 Cr 值与 Δf 一起被保存。此外，在第 33 行，新解种群中的某个个体被试验向量替换，并且待替换个体的索引在第 34 行更新。第 36 行结束个体循环，第 37 行根据 LPSR 更新种群大小。在第 39–41 行收缩种群之前，顶级种群和临时种群在第 38 行被合并、排序，以便将最佳个体保存在顶级种群中。在代结束时，第 42 行使用 $S_F$、$S_{Cr}$ 和 $\Delta f$ 更新记忆单元，第 43 行递增待更新的记忆单元索引，第 44 行对代数执行相同操作。最后，第 45 行结束关于函数评估的主循环，第 46 行返回结果。

L-NTADE 算法的流程图如图 1 所示。

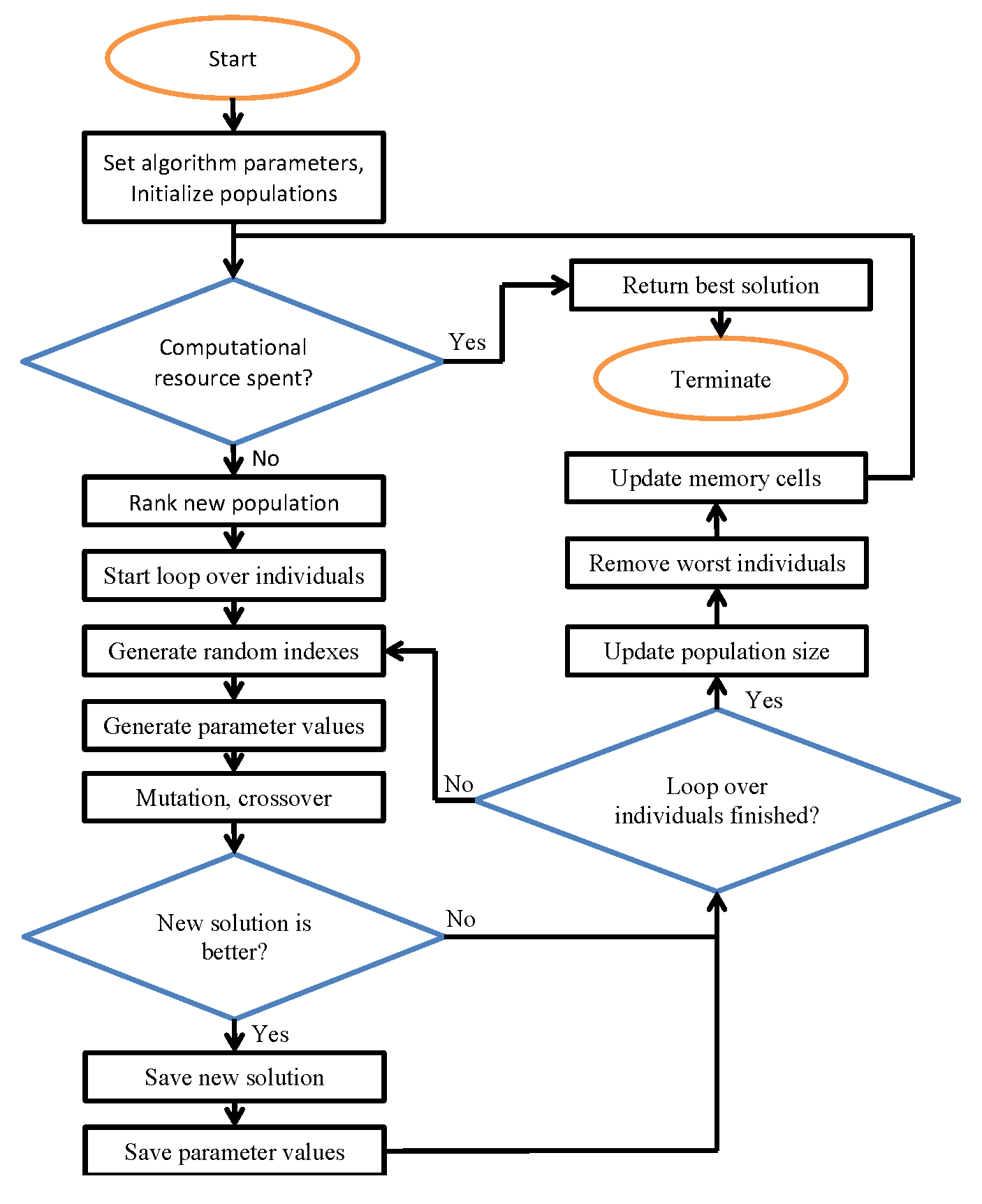
图 1. L-NTADE 算法流程图。

---

4. 实验设置与结果（Experimental Setup and Results）

4.1. 基准测试函数与参数（Benchmark Functions and Parameters）

本研究的主要思想是为 DE 提出一种不同的算法框架，因此针对 L-NTADE 的实验旨在评估其对最新种群和顶级种群大小以及所使用的变异策略的敏感性。实验在两个基准测试集上进行，即 CEC 2017 [35] 和 CEC 2022 [36] 单目标边界约束数值优化问题。选择这两个基准测试是因为它们具有不同的设置，特别是 CEC 2017 的可用函数评估次数比 CEC 2022 少，这使得可以评估所提出算法在不同使用场景下的效率。

CEC 2017 基准测试包含 30 个测试函数，维度为 10、30、50 和 100，计算资源设置为 10,000×维度 次函数评估（相应地，分别为 1×10⁵、3×10⁵、5×10⁵ 和 1×10⁶ 次），每个维度和函数进行 51 次独立运行。

CEC 2022 基准测试包含 12 个测试函数，维度为 10 和 20，计算资源设置为 2×10⁵ 和 1×10⁶ 次评估，每个测试函数和维度进行 30 次独立运行。

所提出的算法在 C++ 中实现，使用 GCC 编译，并在 8 台 AMD Ryzen 3700 PRO 和 7 台 AMD Ryzen 1700（均为 8 核）上运行，操作系统为 Ubuntu Linux 20.04。计算使用 OpenMPI 4.0.3 进行并行化，并使用网络文件系统（NFS）存储结果。结果的后处理、统计测试和可视化在 Python 3.6 中完成。

4.2. 数值结果（Numerical Results）

为了测试 L-NTADE 算法，我们改变了初始种群大小 $N_{max}$、变异策略、选择压力参数 $kp$ 和缩放因子自适应偏差 $pm$。$N_{max}$ 从 15$D$ 变化到 25$D$，步长为 5$D$；考虑了四种变异策略，这导致对于 $D=10$，个体数为 150 到 250，对于 $D=100$，个体数为 1500 到 2500。在大多数情况下，进一步增加种群大小参数会导致性能下降。选择压力应用于所有变异策略中的 $r2$ 索引，排名程序应用于 r-new-to-ptop/h/t 和 r-new-to-ptop/t/n 中的顶级种群，以及另外两种变异中的新解种群。选择压力仅应用于 $r2$，因为初步测试表明，将其应用于其他索引不会带来任何好处。使用了两个控制值，$kp=0$ 和 $kp=3$，前者导致零选择压力（均匀分布）。有偏参数自适应仅应用于缩放因子 $F$，因为先前的研究表明它对 $Cr$ 影响很小。测试的值为 $pm=2$（与 L-SHADE 相同）和 $pm=4$，后者导致更大的 $F$ 值。

为了比较不同 L-NTADE 变体的效率，使用了两种主要工具：采用正态近似和处理并列的曼-惠特尼秩和统计检验来比较一对变体。曼-惠特尼检验中的正态近似意味着结果统计量是标准分数（Z-分数）。这简化了推理过程，并允许直接使用 Z-分数来评估一对算法之间的差异水平。由于每个函数和维度的实验次数相对较多（CEC 2017 为 51 次，CEC 2022 为 30 次），使用正态近似是合理的。因此，在后面的表格和图中，将使用标准分数值以及所有测试函数上的总标准分数，连同胜/平/负的数量来比较两种算法的效率。在需要关于差异显著性的结论的情况下，显著性水平将设置为 0.01。在表 1 中，每个单元格包含在比较 L-NTADE 和在 CEC 2022 竞赛中获得第二名的 NL-SHADE-LBC 时的胜/平/负数量以及所有测试函数上求和的总标准分数。

表 1. L-NTADE 与 NL-SHADE-LBC 在 CEC 2022 基准测试上的比较：曼-惠特尼检验结果及总标准分数

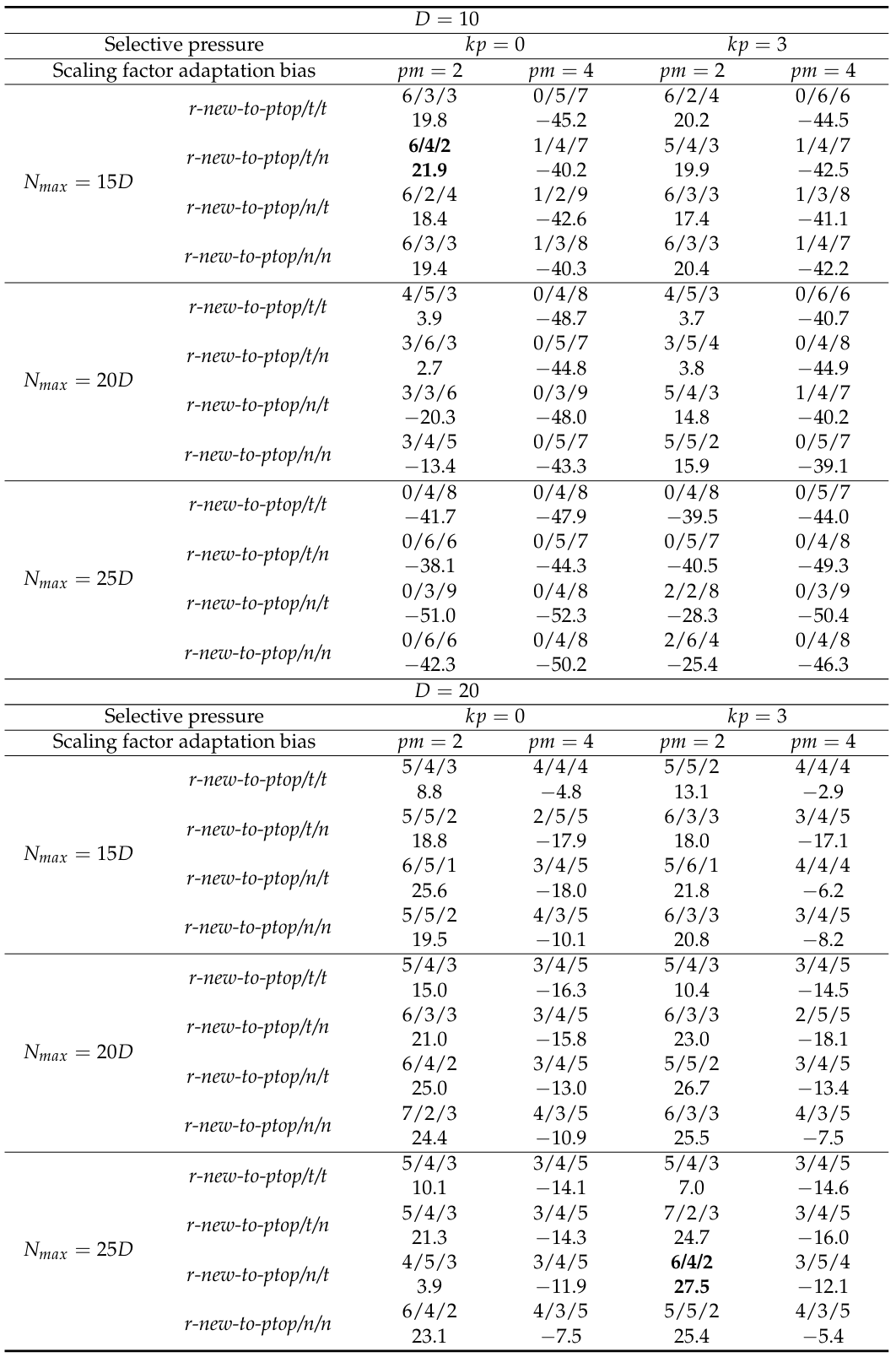
表 1 中的比较表明，所提出的 L-NTADE 算法可能优于或差于 NL-SHADE-LBC，这取决于所使用的参数。例如，应用有偏参数自适应总是导致性能差很多，而选择压力在种群大小和问题维度较大时具有积极影响。至于变异策略，在 10 维情况下，r-new-to-ptop/t/n 显示了最好的结果，但其他策略在有和没有选择压力的情况下也显示出相似的效率。在 20 维情况下，最好的策略是 r-new-to-ptop/n/t 结合选择压力和增加的种群大小。然而，即使没有这两种修改，它也比其他策略表现更好。

表 2 和表 3 包含了在 CEC 2017 基准测试上测试 L-NTADE 的结果。为 L-NTADE 选择的竞争对手是 L-SHADE-RSP 算法，这是在 CEC 2018 竞赛中使用相同基准测试的第二佳方法。测试的参数组合与表 1 相同。

表 2. L-NTADE 与 L-SHADE-RSP 在 CEC 2017 基准测试上的比较（10维与30维）：曼-惠特尼检验结果及总标准分数

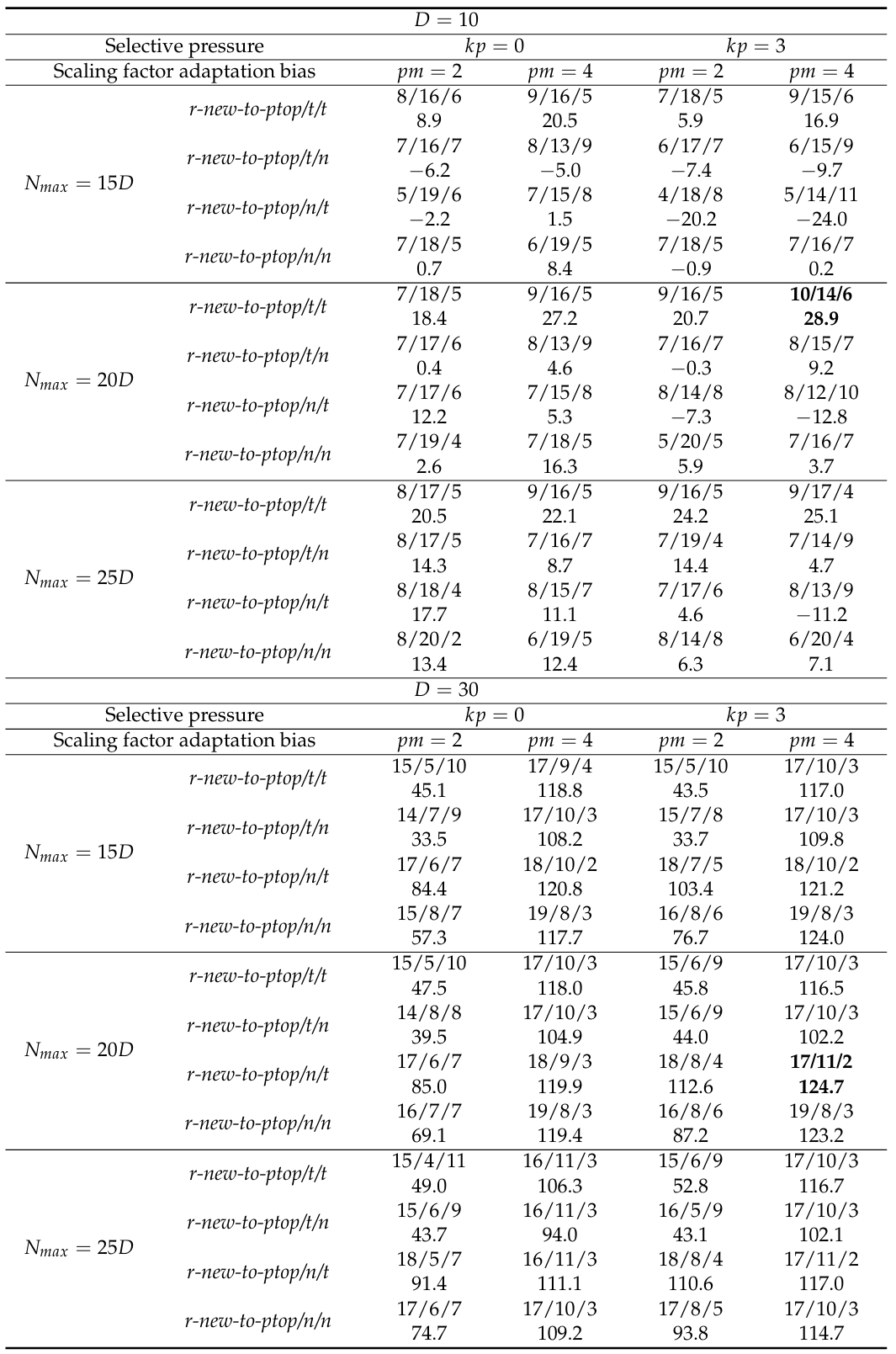
表 3. L-NTADE 与 L-SHADE-RSP 在 CEC 2017 基准测试上的比较（50维与100维）：曼-惠特尼检验结果及总标准分数

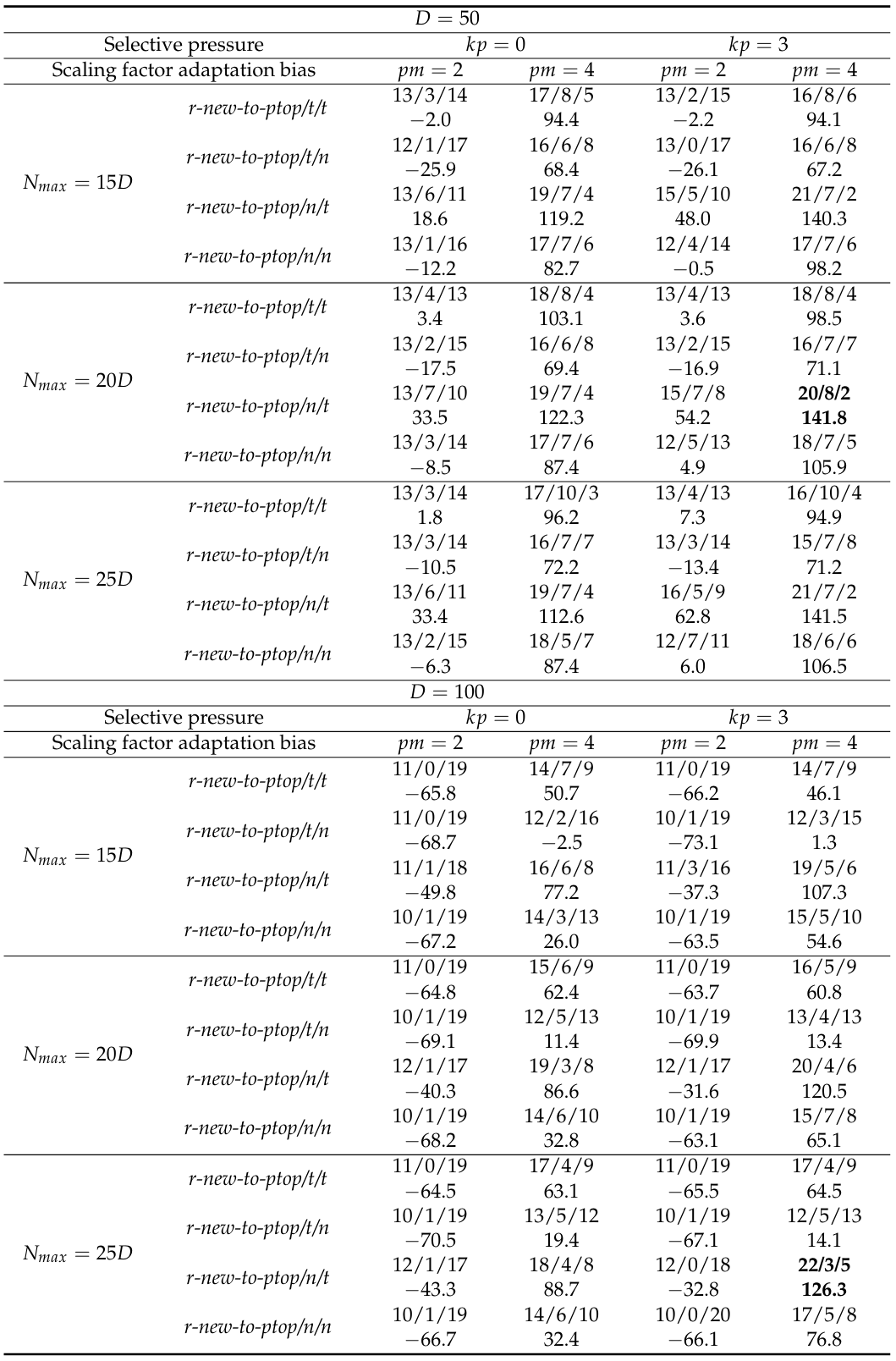
表 2 和表 3 中的结果表明，r-new-to-ptop/n/t 策略结合选择压力和有偏参数自适应在大多数情况下具有最佳性能。然而，在 10 维情况下，r-new-to-ptop/t/t 策略在 $N_{max}=20D$ 时性能最佳，并且较小和较大种群大小的变体之间的差异相当小。这里的其他策略结果差很多。尽管如此，L-NTADE 在大多数情况下优于 L-SHADE-RSP 算法。在 30 维情况下，r-new-to-ptop/n/t 结合 $N_{max}=20D$、选择压力和 $pm=4$ 具有最佳性能，在 30 个函数中的 17 个上战胜了 L-SHADE-RSP，仅在两种情况下失败。这里第二好的策略是 r-new-to-ptop/n/n，它在第二个差分向量中仅使用新解种群中的个体。对于其他变异策略，可以观察到有偏参数自适应显著提高了 L-NTADE 的性能。

在 50 维情况下，表现最佳的变体完全相同，即 r-new-to-ptop/n/t 结合 $N_{max}=20D$、选择压力和 $pm=4$。在这里，可以观察到种群大小的影响很小，这与在 CEC 2022 基准测试上的实验不同。指数基于排名的选择压力在大多数情况下提高了性能，但这种改进相当有限，不像有偏参数自适应带来的改进那么大。在 100 维情况下，相同的结论适用，尽管这里的选择压力影响更大，特别是对于 r-new-to-ptop/n/t 变异策略。

考虑到上述结果，为后续实验选择了以下参数。对于 CEC 2022，$N_{max}=15D$，$kp=0$，$pm=2$，变异策略为 r-new-to-ptop/n/t。对于 CEC 2017，种群大小改为 $N_{max}=20D$，$kp=3$，$pm=4$，变异策略为 r-new-to-ptop/n/t。表 4 显示了 L-NTADE 与 CEC 2022 基准测试上其他替代方法的比较，包括前三名算法（EAdeig [54], NL-SHADE-LBC [55] 和 NL-SHADE-RSP-MID [56]）。表中的值是胜/平/负数量（总标准分数）。

表 4. L-NTADE与CEC 2022竞赛前三名及其他方法的曼-惠特尼检验结果：胜/平/负次数及总标准分数

如表 4 所示，L-NTADE 能够超越参与 CEC 2022 竞赛的最佳算法以及其他方法。求和的标准分数提供了额外信息，使得在胜负数相似的情况下可以观察到不同的性能水平。表 5 显示了在 CEC 2017 基准测试上的比较，使用了相同的符号。

表5. L-NTADE与其他算法在CEC 2017测试集的曼-惠特尼检验结果：胜/平/负次数及总标准分数

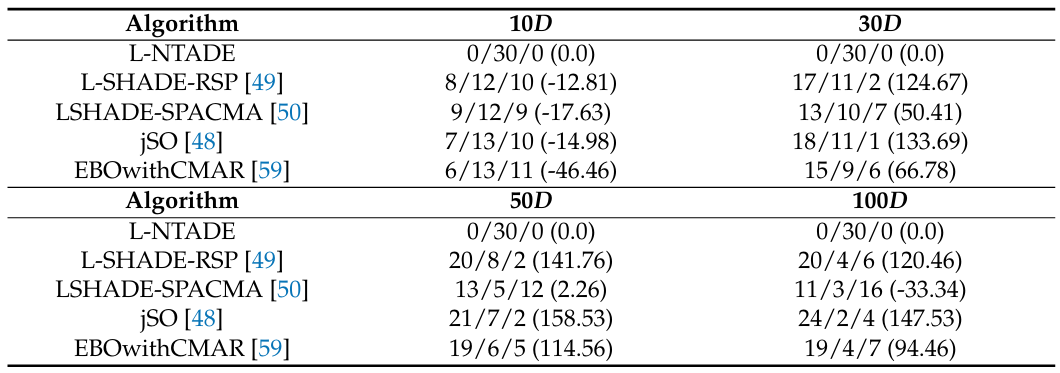
根据表 5，L-NTADE 在 10 维情况下的性能不如其他方法，而在其他维度上则好得多。这可以解释为，对于 10 维情况，最佳变异策略并非表 5 实验中所使用的策略。这样做是为了通用性。在 30 维情况下，L-NTADE 优于所有其他方法，但在 50 维情况下，其性能与 LSHADE-SPACMA 相似。在 100 维情况下，唯一性能更好的算法是 LSHADE-SPACMA，这可能归因于其与 CMA-ES 的混合。

为了评估 L-NTADE 的计算效率，使用了 CEC 2022 基准测试，通过计算计算一组数学表达式所需的时间 ($T0$)、评估第一个测试函数所需的时间 ($T1$) 以及运行算法五次在该测试函数上的平均时间 ($T2$) 来估算时间复杂度。结果值计算为 $(T2-T1)/T0$ [36]。L-NTADE 与 NL-SHADE-RSP 和 NL-SHADE-LBC 的比较结果在表 6 中给出。

表6. L-NTADE与NL-SHADE-LBC、NL-SHADE-RSP在CEC 2022基准测试上的计算复杂度对比

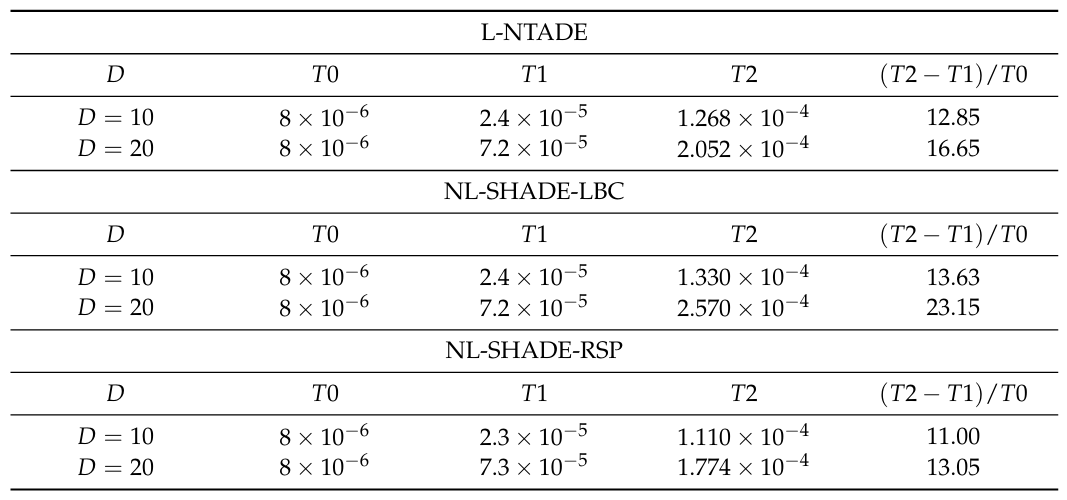
表 6 中的比较表明，L-NTADE 的复杂度与其他类似方法相当，使用额外的种群不会导致显著的计算负担增加。

呈现的实验结果表明，L-NTADE 的算法框架具有一定的潜力，但为了更好地理解其性能原因，进行了一些额外的测试。为了更深入地研究该算法，我们在每一代都为顶级种群和新解种群构建了所有个体之间 pairwise 欧几里得距离的直方图。这些直方图进行了颜色编码，并与平均距离一起显示在热图上。图 2 显示了在 CEC 2017 的 F5（平移旋转的 Rastrigin 函数，10 维）上的这些直方图，图 3 显示了 F17（混合函数 (7)），图 4 显示了 F29（复合函数 (9)）[35]。

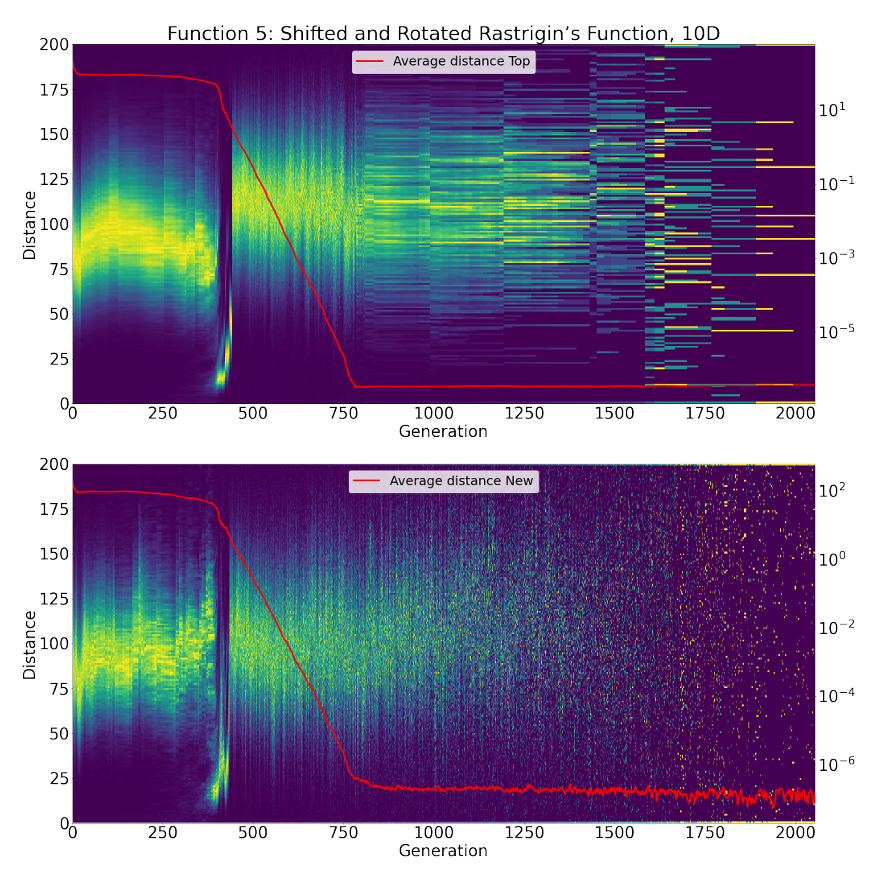
图2. 各代个体间距离直方图热力图（F5函数，CEC 2017测试集，10维）

图 2 中的距离直方图展示了顶级种群和新解种群之间的显著差异。特别是，顶级种群在初始收敛过程后保持相对稳定状态，这可以通过许多水平线看出，每条线对应于局部最小值附近的点（这是 Rastrigin 函数的固有特征）。另一方面，新解种群持续更新，导致产生类似噪声的图像。在最初三分之一阶段，当种群相对相似时，它们将其角色分化为保存有关潜在有趣解的信息和积极寻找更好的解。在搜索结束时，可以观察到顶级种群保留了四个最佳解，而新解种群继续尝试改进。

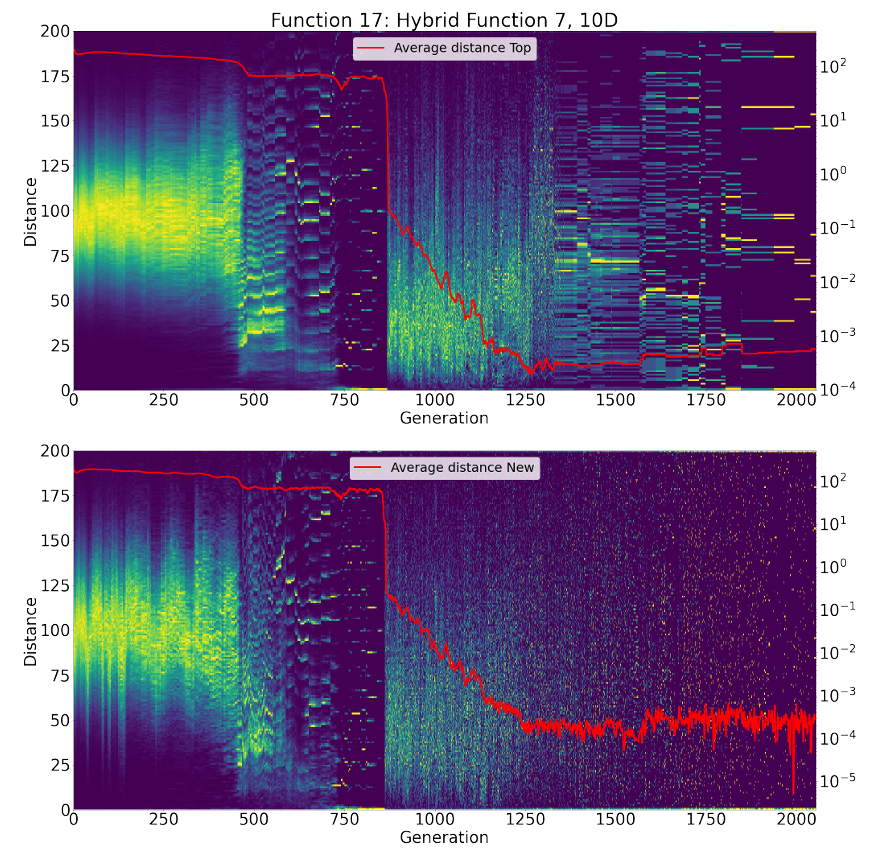
图3. 各代个体间距离直方图热力图（F17函数，CEC 2017测试集，10维）

图 3 显示了类似的情况，两个种群在前 500 代都倾向于收敛，然后分裂成许多对应于局部最优的组。在大约第 900 代，局部搜索的某个区域主导了其他区域（这些区域被删除），另一个主动收敛阶段开始。在第 1300 代之后的某个时刻，顶级种群陷入停滞（再次由水平线可见），但新解种群继续搜索，在搜索过程的后半部分给出了类似的噪声状图像。

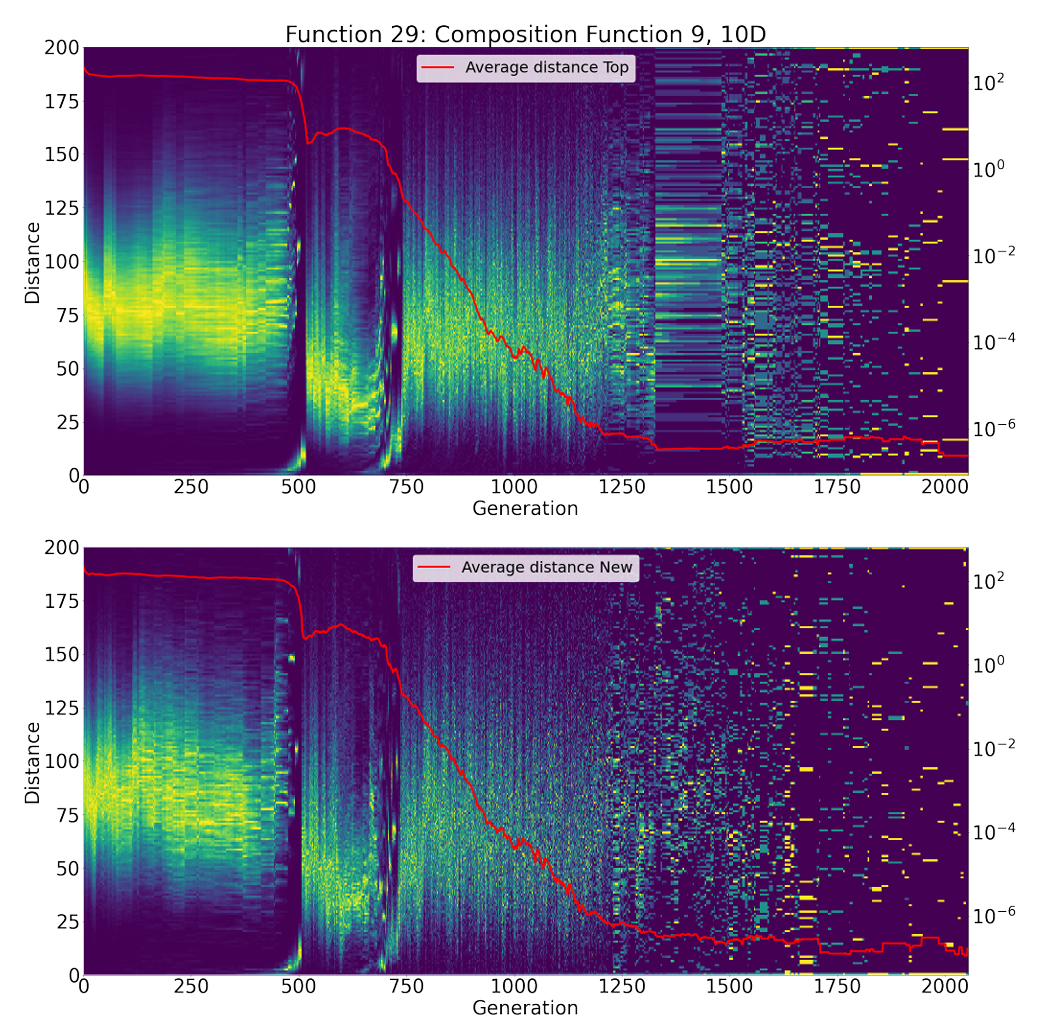
图4. 各代个体间距离直方图热力图（F29函数，CEC 2017测试集，10维）

在图 4 中，可以观察到类似的趋势。然而，现在存在一些阶段，即使是新解种群也可能陷入停滞，例如大约在第 1700 代。尽管如此，搜索过程继续进行，在新解种群中生成不同的解并将其转移到顶级种群中。

---

5. 讨论（Discussion）

前一章节的实验结果表明，UDE算法 [34] 中提出的概念可以被有效利用，例如L-NTADE中的实现方式。所提出的方法对新解种群使用了特定的更新规则，该规则持续用更高效的解替换原有解，但与经典DE选择不同，这里存在更好的解被更差解替换的可能性。与此同时，所有具有高适应度的解始终存储在顶级种群中。新解种群的持续更新，可能是L-NTADE与NL-SHADE-LBC、L-SHADE-RSP及其他方法行为不同的原因之一，这在距离直方图中可以观察到。此外，使用两个种群而非一个，使得L-NTADE能够更有效地解决一些问题，特别是相对复杂的混合函数和复合函数。

就测试的变异策略而言，r-new-to-ptop/n/t、r-new-to-ptop/t/n 和 r-new-to-ptop/n/n 值得关注。在第二个差分向量中组合顶级和新解向量，似乎对最终效率产生了积极影响。此外，总体表现最佳的 r-new-to-ptop/n/t 策略使用了定向的第二个差分向量。第一个差分向量（在随机选择的新解个体和前 pb% 的顶级个体之间）实际上是连接这两个向量的直线上的一个点，该点的位置由 $F$ 控制。第二个差分向量做了类似的事情，即它从新解向量向某个顶级向量迈出一步，也就是朝向更好的解。在L-SHADE-RSP、NL-SHADE-RSP和NL-SHADE-LBC中基于排名的选择压力实验中，使用了类似的变异策略结构，即在第二个差分向量中，步进方向主要朝向更好的解。这一论述也可以得到以下事实的支持：r-new-to-ptop/h/t 在CEC 2017函数的100维情况下能够比大多数其他方法表现更好，并且在一项关于选择压力效应的研究 [42] 中表明，更大的选择压力在高维情况下具有积极影响。与此同时，反其道而行之——当使用 r-new-to-ptop/h/n 时，从更好的解指向随机选择的解——并未带来任何益处。当然，可以为L-NTADE提出其他变异策略，但测试所有可能的变体超出了当前研究的范围。

L-NTADE的缺点之一是其对种群大小非常敏感，正如在CEC 2022上的实验所显示的那样。然而，对于CEC 2017，情况并非如此。此外，对于CEC 2017，选择压力和有偏缩放因子 $F$ 自适应效果很好，但在CEC 2022上却失败了。考虑到这些基准测试的主要区别在于可用的计算资源量，可以得出一个结论：如果计算资源相对较小，大约为10000D，那么应该使用选择压力和有偏参数自适应。否则，应谨慎选择种群大小，但选择压力可能有助于在使用大种群大小时获得更好的结果。经过测试的L-NTADE版本是一个基线版本，可以通过引入为其他基于DE的方法提出的修改来进一步改进。例如：

1. 添加一个存档集并为其制定特定的更新策略；
2. 添加交叉率排序；
3. 引入对 pb% 参数的控制策略；
4. 开发适用于L-NTADE的新参数自适应策略；
5. 开发在算法运行期间切换变异策略的自适应机制；
6. 创建L-NTADE与其他方法的混合算法。

上述改进L-NTADE的可能途径是未来研究的主题。

---

6. 结论（Conclusions）

本研究为差分演化提出了一种新的算法框架，该框架使用两个种群和新的变异策略。所进行的实验表明，所开发的 L-NTADE 是一种极具竞争力的方法，能够在流行的 CEC 2017 和 CEC 2022 基准测试上超越一些最先进的算法，尤其是在复杂的多模态函数上。所提出的算法相对容易实现，因为它是一种非混合方法，并且可以通过添加为其他 DE 方法提出的修改来进一步改进。

与大多数 DE 版本不同，L-NTADE 不使用贪婪选择策略，而是维护两个种群：一个保留最佳解，另一个持续更新。结果和算法行为分析证明了这种方案的优势，即算法使搜索过程始终保持运行。

L-NTADE 的缺点之一是其对种群大小参数的敏感性。然而，所有已知的 DE 算法都存在同样的问题。对所提出算法框架的进一步研究可能包括：试验新解种群中的替换策略，以及为新解种群和顶级种群设置不同的大小并配备特定的控制策略。

参考文献

1. Sloss, A.N.; Gustafson, S. 2019 Evolutionary Algorithms Review. In Proceedings of the Genetic Programming Theory and Practice, East Lansing, MI, USA, 16–19 May 2019.
2. Sinha, A.; Malo, P.; Deb, K. A Review on Bilevel Optimization: From Classical to Evolutionary Approaches and Applications. IEEE Trans. Evol. Comput. 2018, 22, 276–295. [CrossRef]
3. Alkayem, N.F.; Cao, M.; Shen, L.; Fu, R.; Sumarac, D. The combined social engineering particle swarm optimization for real-world engineering problems: A case study of model-based structural health monitoring. Appl. Soft Comput. 2022, 123, 108919. [CrossRef]
4. Alkayem, N.F.; Shen, L.; Al-hababi, T.; Qian, X.; Cao, M. Inverse Analysis of Structural Damage Based on the Modal Kinetic and Strain Energies with the Novel Oppositional Unified Particle Swarm Gradient-Based Optimizer. Appl. Sci. 2022, 12, 11689. [CrossRef]
5. Price, K.; Storn, R.; Lampinen, J. Differential Evolution: A Practical Approach to Global Optimization; Springer: Berlin/Heidelberg, Germany, 2005.
6. Ali, M.; Awad, N.H.; Suganthan, P.; Shatnawi, A.; Reynolds, R. An improved class of real-coded Genetic Algorithms for numerical optimization. Neurocomputing 2018, 275, 155–166. [CrossRef]
7. Maheswaranathan, N.; Metz, L.; Tucker, G.; Sohl-Dickstein, J. Guided Evolutionary Strategies: Escaping the Curse of Dimensionality in Random Search. 2018. Available online: https://openreview.net/forum?id=B1xFxh0cKX (accessed on 5 November 2022).
8. Bonyadi, M.; Michalewicz, Z. Particle Swarm Optimization for Single Objective Continuous Space Problems: A Review. Evol. Comput. 2017, 25, 1–54. [CrossRef] [PubMed]
9. Beyer, H.; Sendhoff, B. Simplify your covariance matrix adaptation evolution strategy. IEEE Trans. Evol. Comput. 2017, 21, 746–759. [CrossRef]
10. Kar, A. Bio inspired computing—A review of algorithms and scope of applications. Expert Syst. Appl. 2016, 59, 20–32. [CrossRef]
11. Skvorc, U.; Eftimov, T.; Korosec, P. CEC Real-Parameter Optimization Competitions: Progress from 2013 to 2018. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 3126–3133.
12. Das, S.; Suganthan, P. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [CrossRef]
13. Das, S.; Mullick, S.; Suganthan, P. Recent advances in differential evolution—An updated survey. Swarm Evol. Comput. 2016, 27, 1–30. [CrossRef]
14. Qin, A.; Suganthan, P. Self-adaptive differential evolution algorithm for numerical optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005; pp. 1785–1791. [CrossRef]
15. dos Santos Coelho, L.; Ayala, H.V.H.; Mariani, V.C. A self-adaptive chaotic differential evolution algorithm using gamma distribution for unconstrained global optimization. Appl. Math. Comput. 2014, 234, 452–459. [CrossRef]
16. Mallipeddi, R.; Suganthan, P.N.; Pan, Q.; Tasgetiren, M.F. Differential evolution algorithm with ensemble of parameters and mutation strategies. Appl. Soft Comput. 2011, 11, 1679–1696. [CrossRef]
17. Gong, W.; Fialho, Á.; Cai, Z.; Li, H. Adaptive strategy selection in differential evolution for numerical optimization: An empirical study. Inf. Sci. 2011, 181, 5364–5386. [CrossRef]
18. Brest, J.; Greiner, S.; Boškovic, B.; Mernik, M.; Žumer, V. Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [CrossRef]
19. Zhang, J.; Sanderson, A.C. JADE: Self-adaptive differential evolution with fast and reliable convergence performance. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 2251–2258.
20. Tanabe, R.; Fukunaga, A. Success-history based parameter adaptation for differential evolution. In Proceedings of the IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; IEEE Press: Piscataway, NJ, USA, 2013; pp. 71–78. [CrossRef]
21. Tanabe, R.; Fukunaga, A. Improving the search performance of SHADE using linear population size reduction. In Proceedings of the IEEE Congress on Evolutionary Computation, CEC, Beijing, China, 6–11 July 2014; pp. 1658–1665. [CrossRef]
22. Piotrowski, A.P.; Napiorkowski, J.J. Step-by-step improvement of JADE and SHADE-based algorithms: Success or failure? Swarm Evol. Comput. 2018, 43, 88–108. [CrossRef]
23. Sun, G.; Xu, G.; Jiang, N. A simple differential evolution with time-varying strategy for continuous optimization. Soft Comput. 2020, 24, 2727–2747. [CrossRef]
24. Sun, G.; Yang, B.; Yang, Z.; Xu, G. An adaptive differential evolution with combined strategy for global numerical optimization. Soft Comput. 2020, 24, 6277–6296. [CrossRef]
25. Huynh, T.N.; Do, D.T.T.; Lee, J. Q-Learning-based parameter control in differential evolution for structural optimization. Appl. Soft Comput. 2021, 107, 107464. [CrossRef]
26. Song, Y.; Wu, D.; Deng, W.; Zhi Gao, X.; Li, T.; Zhang, B.; Li, Y. MPPCEDE: Multi-population parallel co-evolutionary differential evolution for parameter optimization. Energy Convers. Manag. 2021, 228, 113661. [CrossRef]
27. Tan, Z.; Tang, Y.; Li, K.; Huang, H.; Luo, S. Differential evolution with hybrid parameters and mutation strategies based on reinforcement learning. Swarm Evol. Comput. 2022, 75, 101194. [CrossRef]
28. Stanovov, V.; Akhmedova, S.; Semenkin, E. The automatic design of parameter adaptation techniques for differential evolution with genetic programming. Knowl. Based Syst. 2022, 239, 108070. [CrossRef]
29. Stanovov, V.; Akhmedova, S.; Semenkin, E. Neuroevolution for parameter adaptation in differential evolution. Algorithms 2022, 15, 122. [CrossRef]
30. Meng, Z.; Pan, J.S. HARD-DE: Hierarchical ARchive Based Mutation Strategy With Depth Information of Evolution for the Enhancement of Differential Evolution on Numerical Optimization. IEEE Access 2019, 7, 12832–12854. [CrossRef]
31. Brest, J.; Maucec, M.S.; Boškovic, B. Self-adaptive Differential Evolution Algorithm with Population Size Reduction for Single Objective Bound-Constrained Optimization: Algorithm j21. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Krakow, Poland, 28 June–1 July 2021; pp. 817–824.
32. Mohamed, A.; Hadi, A.A.; Mohamed, A.K.; Awad, N.H. Evaluating the Performance of Adaptive GainingSharing Knowledge Based Algorithm on CEC 2020 Benchmark Problems. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8.
33. Zhu, Z.; Chen, L.; Yuan, C.; Xia, C. Global replacement-based differential evolution with neighbor-based memory for dynamic optimization. Appl. Intell. 2018, 48, 3280–3294. [CrossRef]
34. Kitamura, T.; Fukunaga, A. Differential Evolution with an Unbounded Population. In Proceedings of the 2022 IEEE Congress on Evolutionary Computation (CEC), Padua, Italy, 18–23 July 2022.
35. Awad, N.; Ali, M.; Liang, J.; Qu, B.; Suganthan, P. Problem Definitions and Evaluation Criteria for the CEC 2017 Special Session and Competition on Single Objective Bound Constrained Real-Parameter Numerical Optimization; Technical Report; Nanyang Technological University: Singapore, 2016.
36. Kumar, A.; Price, K.; Mohamed, A.; Hadi, A.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2022 Special Session and Competition on Single Objective Bound Constrained Numerical Optimization; Technical Report; Nanyang Technological University: Singapore, 2021.
37. Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [CrossRef]
38. Kitamura, T.; Fukunaga, A. Duplicate Individuals in Differential Evolution. In Proceedings of the 2022 IEEE Congress on Evolutionary Computation (CEC), Padua, Italy, 18–23 July 2022.
39. Kumar, A.; Biswas, P.P.; Suganthan, P.N. Differential evolution with orthogonal array-based initialization and a novel selection strategy. Swarm Evol. Comput. 2022, 68, 101010. [CrossRef]
40. Al-Dabbagh, R.D.; Neri, F.; Idris, N.; Baba, M.S.B. Algorithmic design issues in adaptive differential evolution schemes: Review and taxonomy. Swarm Evol. Comput. 2018, 43, 284–311. [CrossRef]
41. Biedrzycki, R.; Arabas, J.; Jagodzin ́ ski, D. Bound constraints handling in Differential Evolution: An experimental study. Swarm Evol. Comput. 2019, 50, 100453. [CrossRef]
42. Stanovov, V.; Akhmedova, S.; Semenkin, E. Selective Pressure Strategy in differential evolution: Exploitation improvement in solving global optimization problems. Swarm Evol. Comput. 2019, 50, 100463. [CrossRef]
43. Stanovov, V.; Akhmedova, S.; Semenkin, E. Biased Parameter Adaptation in Differential Evolution. Inf. Sci. 2021, 566, 215–238. [CrossRef]
44. Zhang, J.; Sanderson, A.C. JADE: Adaptive differential evolution with optional external archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [CrossRef]
45. Stanovov, V.; Akhmedova, S.; Semenkin, E. Archive update strategy influences differential evolution performance. Adv. Swarm Intell. 2020, 12145, 397–404. 46. Bullen, P. Handbook of Means and Their Inequalities; Springer: Dordrecht, The Netherlands, 2003. [CrossRef]