当前位置：首页 > news >正文

LoRA: Low-Rank Adaptation of Large Language Models及其反思

news 2025/11/11 7:54:08

这篇文章介绍了低秩适配（LoRA）方法，旨在提高大规模预训练语言模型在下游任务中的适配效率。LoRA的核心思想是冻结预训练模型的原始权重，并在模型的各层中注入小型、可训练的低秩分解矩阵。与传统的全量微调方法相比，这种方法大大减少了可训练参数的数量和内存需求。

文章的关键点包括：

效率提升：LoRA提供了显著的计算和存储节省。例如，与传统微调方法相比，它将可训练参数的数量减少了10,000倍，GPU内存需求最多减少了3倍。最重要的是，LoRA不会增加推理延迟，而适配器方法通常会在部署过程中引入延迟。
秩缺失：作者证明，即使注入矩阵的秩非常低（例如，r=1或r=2），LoRA在各种模型（如RoBERTa、GPT-2、GPT-3）和任务上都表现良好，表明语言模型的适配具有内在的低秩结构。这表明，少量特定任务的参数就能有效捕捉必要的适配信息。
与其他方法的比较：LoRA在许多参数高效的微调方法中表现优异，甚至超越了适配器层、前缀调优和全量微调方法，尽管它的可训练参数数量远少于这些方法。特别是在像GPT-3 175B这样的超大规模模型中，LoRA在保持高模型质量的同时，显著减少了资源的使用。
实际优势：LoRA的低秩矩阵可以高效存储和在任务之间切换，能够快速实现任务切换，而无需重新训练或存储独立的完整模型。它还减少了训练大规模模型所需的硬件资源，使得更多用户能够使用。
实验与结果：文章包括了在多个基准（如GLUE、WikiSQL、SAMSum和E2E NLG Challenge）上的实验，结果显示，LoRA可以在参数少的情况下，取得与其他方法相当或更好的表现，且更加高效。

作者发布了LoRA的实现代码，支持与PyTorch模型的集成，并提供了RoBERTa、DeBERTa和GPT-2等模型的检查点。

在这篇文章中，LoRA（低秩适配）方法通过将低秩分解矩阵注入到模型的各层中来进行高效适配，并冻结原有的预训练权重。下面我将详细介绍LoRA方法的核心内容，特别是图像部分，并提供相应图的编号。

LoRA方法的核心设计

LoRA方法的基本思想是通过低秩分解矩阵来替代传统的微调方法，减少计算和存储的需求，同时不引入推理延迟。具体来说，LoRA将模型的权重矩阵（例如自注意力模块的查询、键、值矩阵）进行低秩分解，仅训练低秩分解的矩阵，保留原始的预训练权重不变。这样一来，适配模型时所需训练的参数大大减少。

在LoRA中，预训练的权重矩阵 $W_0$ 被分解为低秩矩阵 $A$ 和 $B$ ，更新矩阵为 $ΔW=A⋅B\Delta W = A \cdot B$ ，其中 $A$ 是 $\times r$ 维的矩阵， $B$ 是 $\times k$ 维的矩阵， $r$ 表示秩。通过这种方式，仅需要训练 $A$ 和 $B$ ，而原始的 $W_0$ 保持不变。

图像部分的解释

在文章中，图像主要展示了LoRA方法的具体实现方式及其在模型中的应用。以下是相关图像的描述和编号。
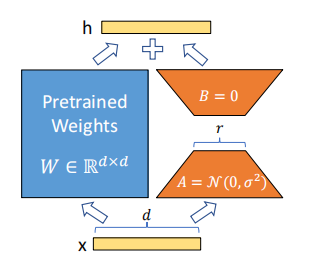
在这里插入图片描述

图1：LoRA的参数化更新

图1展示了LoRA方法的关键设计，主要是权重矩阵的低秩分解和其更新机制。具体来说，LoRA方法通过将原始的预训练权重矩阵 $W_0$ 加上低秩更新矩阵 $ΔW=A⋅B\Delta W = A \cdot B$ ，来进行模型的适配。图中展示了如何通过这两个低秩矩阵 $A$ 和 $B$ 来更新模型的权重，避免了对原始权重矩阵进行全量微调。整个过程通过图1清晰展示了矩阵分解的方式。
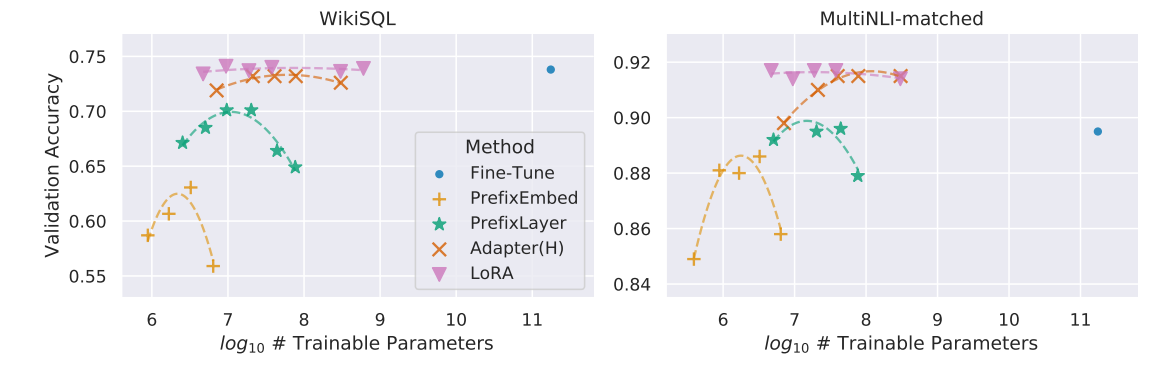
在这里插入图片描述

图2：GPT-3 175B的验证准确率与训练参数的关系

图2展示了不同适配方法在GPT-3 175B模型上训练时，验证准确率与可训练参数数量之间的关系。图中展示了LoRA方法在任务WikiSQL和MNLI-m的验证准确率与其他方法（如全量微调、前缀嵌入等）相比，LoRA在训练参数少的情况下仍能保持较高的性能，证明了LoRA的高效性和良好的扩展性。
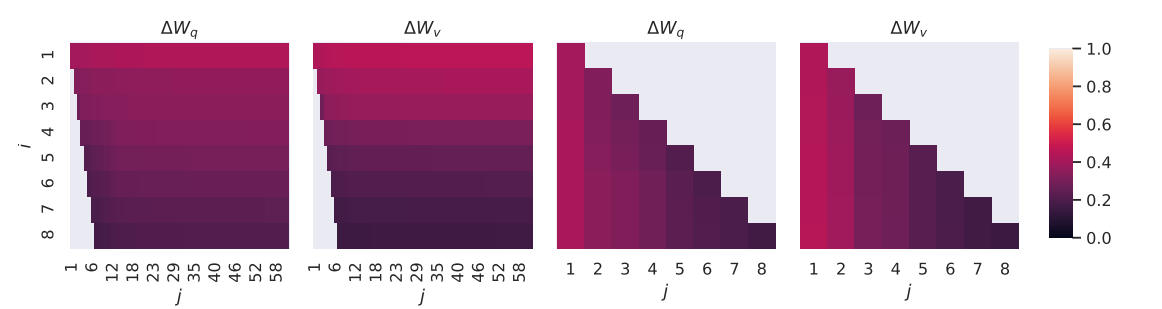
在这里插入图片描述

图3：低秩适配矩阵的子空间相似性

图3通过比较不同秩（ $r = 8$ 和 $r = 64$ ）的适配矩阵 $A$ 和 $B$ 在不同层之间的子空间相似性，展示了低秩适配矩阵之间的重叠度。通过奇异值分解，图中展示了不同秩的矩阵在适配过程中如何选择特定方向，以及这些方向如何影响模型的最终性能。图3揭示了LoRA适配矩阵在高维空间中如何有效地压缩并捕获任务特定的方向。
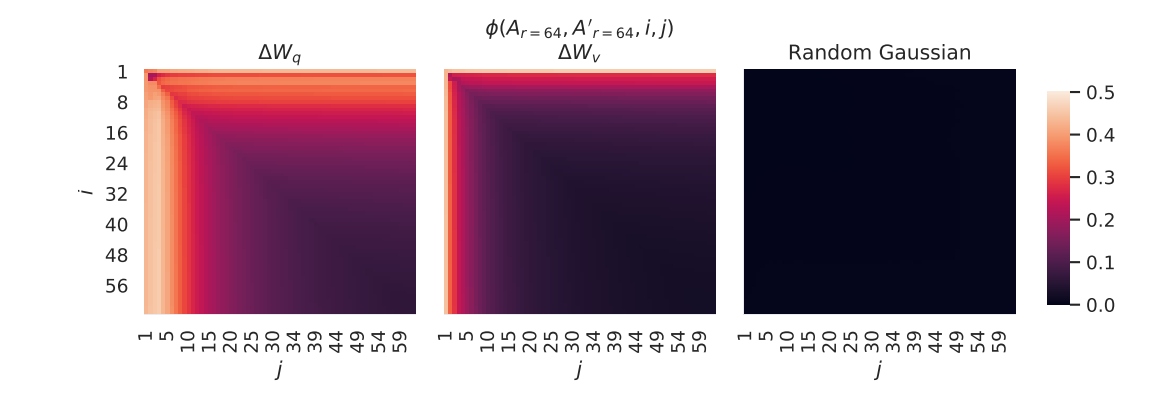
在这里插入图片描述

图4：不同随机种子下的适配矩阵子空间相似性

图4展示了在不同随机种子下，LoRA方法在适配过程中如何生成一致的适配矩阵。通过对比不同随机种子生成的适配矩阵子空间相似性，图中展示了LoRA方法的稳定性，即使在随机初始化下，LoRA也能够保持较高的相似性，表明其适应能力和稳定性。
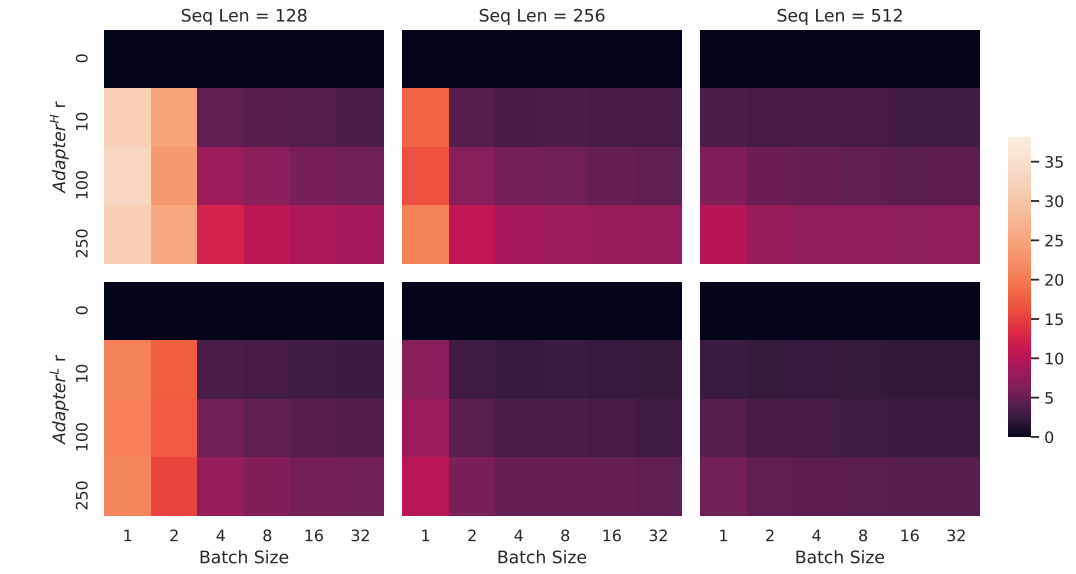
在这里插入图片描述

图5：不同秩对E2E NLG Challenge的影响

图5展示了不同秩（r=1, 2, 4, 8, 16, 32等）在E2E NLG Challenge任务中的验证损失和其他评估指标（如BLEU、NIST、ROUGE等）的表现。图中的结果表明，较低的秩（如r=4或r=8）能够在保留性能的同时有效减少参数数量，而更高的秩则不会显著提高性能，反而可能带来不必要的计算开销。

其他实验结果

论文还通过大量的实验（包括GLUE、WikiSQL、SAMSum、E2E NLG Challenge等）验证了LoRA在多个任务中的表现。实验结果显示，LoRA不仅在参数效率上优于其他方法，而且在不牺牲性能的情况下大幅减少了计算资源的使用。

结论

LoRA通过低秩分解矩阵的设计，提供了一种高效的适配方法。与传统的全量微调和其他轻量化方法相比，LoRA在减少训练参数和内存占用的同时，保持了模型性能，尤其适用于大规模语言模型的快速任务切换和生产环境中的应用。未来的研究可以进一步探索LoRA与其他适配策略的结合，并研究如何更有效地选择适配矩阵和调整秩。

1. DoWhy的优势

DoWhy 在因果推理中的使用相较于传统因果推理方法（如基于规则的模型、简单的回归模型或图形模型）有多个优势：

因果图建模：DoWhy基于因果图（Causal Graphs）模型，能够明确表示因果关系。与传统方法不同，DoWhy允许你明确地定义并操作因果图，帮助你理解变量之间的因果关系，并进行干预（interventions）。
因果推理框架：DoWhy提供了统一的因果推理框架，它结合了因果图建模、潜在变量模型、随机控制实验等技术，为因果效应的估计提供多种方法。它支持不同的推理方法，如回归、倾向评分匹配（Propensity Score Matching）等，同时可以通过模型的假设验证步骤来确保推理的可靠性。
假设验证：DoWhy不仅用于估计因果效应，还提供了用于验证因果假设的方法。它可以帮助用户检查因果图中的假设是否成立，确保推理的结论不受潜在偏差的影响。
多种算法支持：DoWhy支持多种因果推理算法，例如：回归模型、倾向评分匹配、逆概率加权法（IPW）、因果图的图形模型算法等。通过这些算法，你可以对因果关系进行系统的分析。
与机器学习方法结合：DoWhy可以与常见的机器学习方法（如线性回归、决策树、神经网络等）结合，进一步提升因果推理的准确性。例如，通过回归模型来估计因果效应时，DoWhy可以帮助你处理潜在的混杂因子，从而获得更可靠的结果。

2. 传统因果推理方法 vs. DoWhy

传统因果推理方法：许多传统的因果推理方法依赖于简单的统计学推断，如线性回归、Pearson相关性等。它们通常假设变量之间的关系是线性或静态的，且未能有效处理复杂的因果结构和潜在的偏差（例如混杂因子）。
DoWhy：相比之下，DoWhy更加灵活且具备自动化功能，它允许用户更清晰地定义因果关系图，并进行复杂的因果推理分析。它的框架使得因果推理的模型更具可解释性，并且可以验证假设，增强了因果推理的可信度。

3. DoWhy 在因果推理中的应用

因果效应估计：DoWhy能够准确估计各种因果效应，比如因果推断中的平均处理效应（ATE）和条件处理效应（CATE）。在某些情境下，DoWhy结合回归方法和图模型能够提高因果效应的估计准确性。
时间关系抽取：在时间关系抽取的任务中，DoWhy可以帮助模型捕捉时间序列中的因果关系。例如，理解事件A是否引起了事件B的发生，可以通过DoWhy结合因果图进行建模和推理，从而帮助提高时间序列数据中的因果关系抽取的准确性。
政策干预分析：DoWhy非常适合用来评估政策干预的因果影响。通过因果推理框架，可以模拟干预政策的影响，评估不同干预方案下的效果。

4. DoWhy的挑战与局限

尽管DoWhy是一个强大的工具，它也有一定的挑战和局限性：

模型假设依赖：DoWhy依赖于明确的因果图和假设，而这些假设在很多实际场景中并不总是准确的。如果因果图的构建存在偏差或错误，推理结果也会受到影响。
数据需求：DoWhy要求较高质量的训练数据。如果数据本身存在偏差或者不完全，因果推理的结果也可能不可靠。
复杂性：对于非常复杂的因果关系，DoWhy可能需要较为复杂的因果图结构，理解和维护这些图可能是一个挑战，特别是在多维度、高复杂度的任务中。

5. 结合LoRA与DoWhy进行因果推理

如果你考虑将 LoRA 和 DoWhy 结合使用，可以在以下几个方面发挥其优势：

LoRA优化因果推理模块：使用LoRA来微调模型中的因果推理模块，使其能够更高效地适应因果推理任务。LoRA的低秩适配可以有效减少因果推理模型的计算成本，并通过因果推理的方式提升模型对时间关系等复杂结构的理解。
多任务学习：可以通过LoRA训练多个因果推理任务的模型，例如同时进行因果效应估计、因果关系建模和时间关系抽取，这样能够提升因果推理在多个任务中的表现。
验证因果假设：通过DoWhy提供的因果假设验证工具，确保LoRA微调后得到的模型在因果推理方面的假设是合理的，从而提升因果推理结果的可靠性。

📚 推荐书目

Causal Inference and Discovery in Python: Unlock the secrets of modern causal machine learning with DoWhy, EconML, PyTorch and more（Aleksander Molak 著，2023年）
- 详细介绍了因果推理的基础概念（结构因果模型、干预、反事实等）+ 在 Python 中用 DoWhy、EconML 等工具实现。 (Google Books)
- 目录中包括“4‑步因果推理过程”（model → identify → estimate → refute）等内容。 (Google Books)
- 获取方式：在出版社官网有纸书和电子版出售。 (Packt)
Causal Inference for Everyone: A Beginner’s Guide to Python Tools and Causal Inference（入门级书，覆盖 DoWhy、CausalML、EconML）
- 针对初学者，结合 Python 工具，包含 DoWhy 使用。 (Amazon)
- 适合你这种希望“基础、简单易懂”解释的背景。
Causality: Models, Reasoning, and Inference（Judea Pearl 著）
- 虽然不专门讲 DoWhy，但这是因果推理领域经典教材，奠定了很多理论基础。 (Wikipedia)
- 推荐在你愿意深入理论的话读。

✅ 合法下载 / 获取方式

上述第一本书在其出版社官网有 电子版 + 纸本 出售（“Print & eBook”选项） (Packt)
图书馆／学校图书馆通常也有电子版或实体版可借。
开源文档／教程：DoWhy 的官方 GitHub + 文档站点也提供很多免费教学内容。 (GitHub)

将 因果推理 整合到 LoRA（Low-Rank Adaptation）方法中，尤其是针对 时间关系抽取 的任务，理论上可以显著提升模型的性能。这是因为因果推理能够帮助模型理解事件之间的因果关系和时间顺序，而时间关系抽取本质上是一个涉及事件顺序和时间依赖性的任务。

1. LoRA与因果推理结合的理论贡献

LoRA通过注入低秩矩阵进行任务适配，从而在保留原有预训练模型权重的情况下，减少计算资源和内存占用。因果推理，尤其是时间关系的因果推理，主要有以下贡献：

时间顺序的理解：因果推理可以明确事件的因果关系，例如，“事件A发生导致事件B发生”或“事件A发生后，事件B才发生”。这有助于模型在抽取时间关系时，不仅仅根据事件之间的顺序，还能理解两者之间的因果联系。
干预与反事实分析：因果推理能够对时间事件进行干预，模拟不同的时间假设下事件的结果。例如，如果事件A提前发生，事件B是否仍然会在预定时间发生？这种推理能够帮助模型从不同的时间角度提取时间关系。
泛化能力：通过因果推理，模型能够捕捉到更为细致的时间依赖性，使得时间抽取不仅仅局限于顺序问题，而能够理解时间的因果影响，提升模型在处理复杂时间序列时的泛化能力。

2. LoRA与因果推理结合的实现方式

将因果推理与LoRA结合，通常可以通过以下方式进行：

在LoRA的适配层中集成因果推理模块：可以设计一个因果推理层，作为LoRA微调的一个子模块，通过低秩矩阵的方式来适应因果推理模型的特征。这使得模型不仅仅学习事件之间的时间关系，还能够识别它们之间的因果依赖性。
因果图与时间序列模型结合：LoRA可以被应用于因果图的训练过程中，从而能够在因果图的框架下进行时间关系的建模和推理。

3. 时间关系抽取任务的背景

时间关系抽取任务的目标是从文本中识别出事件的时间信息，并确定这些事件之间的时间顺序或依赖关系。例如，给定以下句子：

“事件A发生后，事件B才发生。”
- 事件A和事件B的时间关系是因果关系，并且事件A发生在事件B之前。

通过因果推理，模型不仅能从文本中提取出“事件A在事件B之前”这样的顺序，还能够理解“事件A是事件B发生的前提条件”。

4. Python代码实现

以下是一个基于 LoRA 和因果推理的时间关系抽取模型的示例代码。为了便于说明，代码会使用 DoWhy 库进行因果推理，并结合 LoRA 来微调模型。

安装所需库

pip install dowhy transformers torch

代码实现示例

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from dowhy import CausalModel
from transformers import AutoModelForSequenceClassification, AutoTokenizer, Trainer, TrainingArguments
from peft import LoraConfig, get_peft_model# 示例文本数据（包含时间关系标注）
data = pd.DataFrame({"text": ["Event A happened before Event B.","Event A triggered Event B.","Event A was followed by Event B.","Event A and Event B happened at the same time."],"label": [1, 1, 1, 0]  # 1表示事件之间存在因果关系，0表示没有
})# 将数据划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(data['text'], data['label'], test_size=0.2)# 载入预训练的BERT模型和tokenizer
model_name = "bert-base-uncased"
model = AutoModelForSequenceClassification.from_pretrained(model_name, num_labels=2)
tokenizer = AutoTokenizer.from_pretrained(model_name)# 数据编码
def encode_function(texts):return tokenizer(texts, padding=True, truncation=True, return_tensors='pt')train_encodings = encode_function(X_train.tolist())
test_encodings = encode_function(X_test.tolist())# LoRA微调配置
lora_config = LoraConfig(r=4,  # 低秩矩阵的秩lora_alpha=16,  # 缩放系数target_modules=["attention.self.query", "attention.self.key", "attention.self.value"],lora_dropout=0.1
)# 使用LoRA进行微调
model = get_peft_model(model, lora_config)# 设置训练参数
training_args = TrainingArguments(output_dir='./results',evaluation_strategy='epoch',learning_rate=2e-5,per_device_train_batch_size=16,per_device_eval_batch_size=64,num_train_epochs=3
)trainer = Trainer(model=model,args=training_args,train_dataset=train_encodings,eval_dataset=test_encodings
)trainer.train()# 使用DoWhy进行因果推理分析
causal_model = CausalModel(data=data,treatment='text',  # 这里将text作为治疗变量（模拟的因果关系变量）outcome='label',  # 目标变量为是否存在因果关系common_causes=['EventA', 'EventB'],  # 假设事件A和事件B为共同原因
)# 识别因果关系并进行推理
causal_model.view_model()
identified_estimand = causal_model.identify_effect()
causal_effect = causal_model.estimate_effect(identified_estimand, method_name="backdoor.propensity_score_matching")print(f"Causal Effect: {causal_effect}")