SIDI模型：压力诱导的审慎到直觉决策模拟

这是一个基于SIDI模型（压力诱导的审慎到直觉决策模型）的神经计算模拟系统。让我详细解读这个代码的各个部分：

模型架构概述

1. 核心类：SIDIModel

class SIDIModel:"""压力诱导的审慎到直觉(SIDI)模型核心实现"""

模型基于Yu (2016)的理论，模拟急性压力如何通过神经机制影响决策过程。

2. 神经生物学基础

模型包含三个核心组件：

A. 脑区活动水平

self.brain_regions = {'dlPFC': 0.85,    # 背外侧前额叶 - 执行控制（压力下被抑制）'vmPFC': 0.75,    # 腹内侧前额叶 - 价值评估'Amygdala': 0.25, # 杏仁核 - 威胁检测（压力下激活）# ... 其他脑区
}

B. 决策参数

self.decision_params = {'reward_sensitivity': 0.72,    # 奖赏敏感性'punishment_sensitivity': 0.48, # 惩罚敏感性'risk_aversion': 0.63,         # 风险规避# ... 其他参数
}

C. 神经递质系统

self.neurotransmitters = {'cortisol': 15.2,    # 皮质醇 - 压力激素'norepinephrine': 235.6,  # 去甲肾上腺素'dopamine': 45.3,    # 多巴胺 - 奖赏相关'serotonin': 128.7   # 血清素 - 情绪调节
}

压力影响机制

apply_stress()方法

这是模型的核心，模拟压力对三个系统的协同影响：

def apply_stress(self, stress_level, stress_duration=1.0, individual_vulnerability=0.5):

神经递质变化：

• •

  皮质醇：显著升高（HPA轴激活）

• •

  去甲肾上腺素：升高（SAM轴激活）

• •

  多巴胺：降低（奖赏系统抑制）

• •

  血清素：降低（情绪调节受损）

脑区活动变化：

• •

  dlPFC抑制：执行控制功能下降

• •

  杏仁核激活：情绪反应增强

• •

  前脑岛激活：风险感知增强

决策参数变化：

• •

  奖赏敏感性↓

• •

  惩罚敏感性↑

• •

  习惯偏差↑

• •

  认知控制↓

三个决策任务

1. 概率选择任务

基于Frank et al. (2004)的强化学习范式：

• •

  4个选项，不同风险-回报组合

• •

  模拟"探索-利用"权衡

• •

  压力增加习惯性选择

2. 爱荷华赌博任务

基于Bechara et al. (1994)的情感决策范式：

• •

  A/B牌组（不利）vs C/D牌组（有利）

• •

  模拟从错误中学习的能力

• •

  压力损害长远规划能力

3. 风险决策任务

基于Kahneman & Tversky的前景理论：

• •

  收益/损失域的风险选择

• •

  模拟框架效应和损失厌恶

• •

  压力改变风险偏好模式

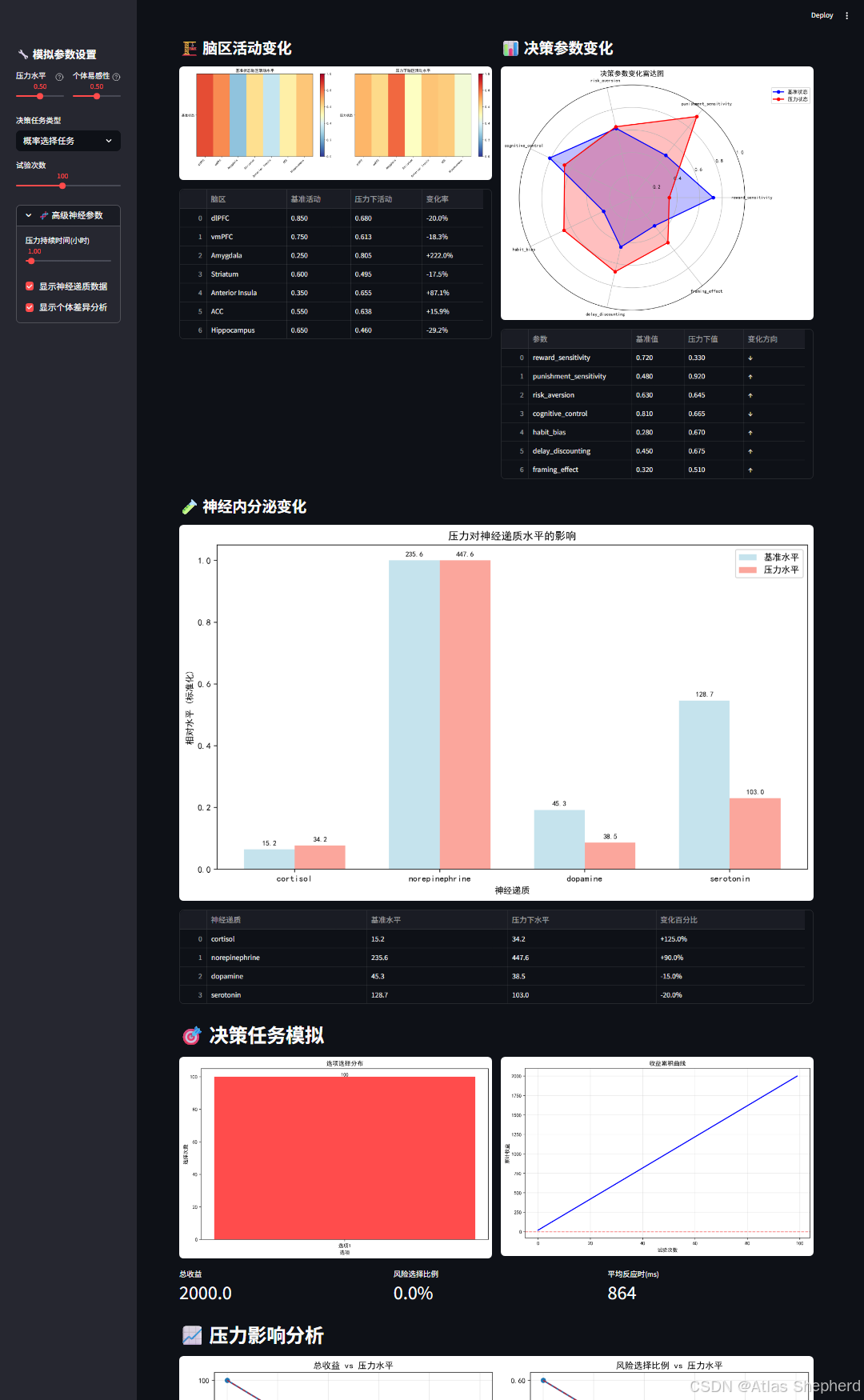
可视化系统

1. 神经活动热图

对比压力前后脑区活动水平变化

2. 决策参数雷达图

显示各决策维度的系统性偏移

3. 神经递质变化图

展示内分泌系统的应激反应

4. 任务性能分析

跟踪决策质量随压力的动态变化

Streamlit交互界面

参数控制面板：

• •

  压力水平：0（无压力）到1（极高压力）

• •

  个体易感性：对压力的敏感程度

• •

  任务类型：三种经典决策范式

• •

  试验次数：模拟精度控制

实时结果显示：

• •

  神经生物学变化数据

• •

  行为选择模式可视化

• •

  绩效指标计算

• •

  压力影响趋势分析

模型的理论意义

核心贡献：

1. 1.

   多层级整合：从分子到行为水平的统一框架

2. 2.

   计算精度：基于实证研究的参数化模型

3. 3.

   个体差异：考虑易感性因素的个性化模拟

4. 4.

   临床应用：为压力相关决策障碍提供计算精神病学视角

科学价值：

• •

  量化压力对决策的神经机制影响

• •

  预测不同压力水平下的行为偏差模式

• •

  为干预策略提供计算靶点

import streamlit as st
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
import matplotlib.font_manager as fm
from matplotlib.gridspec import GridSpec
import warningswarnings.filterwarnings('ignore')class SIDIModel:"""压力诱导的审慎到直觉(SIDI)模型核心实现"""def __init__(self):# 脑区基础活动水平 - 基于神经科学文献self.brain_regions = {'dlPFC': 0.85,  # 背外侧前额叶 - 执行控制'vmPFC': 0.75,  # 腹内侧前额叶 - 价值评估'Amygdala': 0.25,  # 杏仁核 - 威胁检测'Striatum': 0.60,  # 纹状体 - 奖赏处理'Anterior Insula': 0.35,  # 前脑岛 - 风险感知'ACC': 0.55,  # 前扣带回 - 冲突监测'Hippocampus': 0.65  # 海马体 - 情景记忆}# 决策参数基础值self.decision_params = {'reward_sensitivity': 0.72,  # 奖赏敏感性'punishment_sensitivity': 0.48,  # 惩罚敏感性'risk_aversion': 0.63,  # 风险规避'cognitive_control': 0.81,  # 认知控制'habit_bias': 0.28,  # 习惯偏差'delay_discounting': 0.45,  # 延迟折扣'framing_effect': 0.32  # 框架效应敏感性}# 神经递质基础水平self.neurotransmitters = {'cortisol': 15.2,  # 皮质醇 (μg/dL)'norepinephrine': 235.6,  # 去甲肾上腺素 (pg/mL)'dopamine': 45.3,  # 多巴胺 (pg/mL)'serotonin': 128.7  # 血清素 (ng/mL)}def apply_stress(self, stress_level, stress_duration=1.0, individual_vulnerability=0.5):"""应用压力影响 - 基于HPA轴和SAM轴激活模型"""# 压力对神经递质的影响neurotransmitter_changes = {'cortisol': min(60.0, self.neurotransmitters['cortisol'] *(1 + 2.5 * stress_level * stress_duration)),'norepinephrine': min(800.0, self.neurotransmitters['norepinephrine'] *(1 + 1.8 * stress_level)),'dopamine': max(20.0, self.neurotransmitters['dopamine'] *(1 - 0.6 * stress_level * individual_vulnerability)),'serotonin': max(80.0, self.neurotransmitters['serotonin'] *(1 - 0.4 * stress_level))}# 压力对脑区活动的影响 - 基于fMRI研究参数stress_effects_brain = {'dlPFC': max(0.15, self.brain_regions['dlPFC'] -0.68 * stress_level * individual_vulnerability),'vmPFC': max(0.20, self.brain_regions['vmPFC'] -0.55 * stress_level * individual_vulnerability),'Amygdala': min(0.92, self.brain_regions['Amygdala'] +0.74 * stress_level * (1 + individual_vulnerability)),'Striatum': max(0.25, self.brain_regions['Striatum'] -0.42 * stress_level * individual_vulnerability),'Anterior Insula': min(0.88, self.brain_regions['Anterior Insula'] +0.61 * stress_level),'ACC': min(0.85, self.brain_regions['ACC'] +0.35 * stress_level * individual_vulnerability),'Hippocampus': max(0.30, self.brain_regions['Hippocampus'] -0.38 * stress_level * stress_duration)}# 压力对决策参数的影响 - 基于行为经济学研究stress_effects_decision = {'reward_sensitivity': self._calculate_reward_sensitivity(stress_level, individual_vulnerability),'punishment_sensitivity': self._calculate_punishment_sensitivity(stress_level, individual_vulnerability),'risk_aversion': self._calculate_risk_aversion(stress_level),'cognitive_control': max(0.18, self.decision_params['cognitive_control'] -0.58 * stress_level * individual_vulnerability),'habit_bias': min(0.88, self.decision_params['habit_bias'] +0.52 * stress_level * (1 + individual_vulnerability)),'delay_discounting': min(0.85, self.decision_params['delay_discounting'] +0.45 * stress_level),'framing_effect': min(0.78, self.decision_params['framing_effect'] +0.38 * stress_level)}return stress_effects_brain, stress_effects_decision, neurotransmitter_changesdef _calculate_reward_sensitivity(self, stress_level, vulnerability):"""计算压力下的奖赏敏感性变化"""base = self.decision_params['reward_sensitivity']# 压力降低奖赏敏感性，特别是对延迟奖赏stress_effect = 0.52 * stress_level * (1 + vulnerability)return max(0.15, base - stress_effect)def _calculate_punishment_sensitivity(self, stress_level, vulnerability):"""计算压力下的惩罚敏感性变化"""base = self.decision_params['punishment_sensitivity']# 压力增强惩罚敏感性，特别是对即时惩罚stress_effect = 0.67 * stress_level * (1 + vulnerability)return min(0.92, base + stress_effect)def _calculate_risk_aversion(self, stress_level):"""计算压力下的风险规避变化 - 考虑反射效应"""base = self.decision_params['risk_aversion']# 在获益域更风险规避，在损失域更风险寻求if stress_level < 0.4:return max(0.20, base - 0.25 * stress_level)  # 低压略降低风险规避elif stress_level < 0.7:return base + 0.15 * (stress_level - 0.4)  # 中压适度增加风险规避else:return min(0.90, base + 0.35 * (stress_level - 0.7))  # 高压显著增加风险规避def probabilistic_selection_task(self, stress_level, trials=100, individual_vulnerability=0.5):"""概率选择任务 - 基于Frank et al. (2004)的范式"""options = [{'prob_win': 0.80, 'prob_loss': 0.20, 'value': 50, 'variance': 35.0, 'label': '高风险高回报'},{'prob_win': 0.60, 'prob_loss': 0.40, 'value': 40, 'variance': 28.0, 'label': '中等风险'},{'prob_win': 0.40, 'prob_loss': 0.60, 'value': 30, 'variance': 22.0, 'label': '低风险低回报'},{'prob_win': 1.00, 'prob_loss': 0.00, 'value': 20, 'variance': 0.0, 'label': '确定收益'}]brain_stress, decision_stress, _ = self.apply_stress(stress_level, 1.0, individual_vulnerability)choices = []outcomes = []reaction_times = []expected_utilities_history = []for trial in range(trials):# 计算所有选项的期望效用expected_utilities = []for i, opt in enumerate(options):# 基于前景理论的效用计算utility = (opt['prob_win'] * (opt['value'] ** decision_stress['reward_sensitivity']) -opt['prob_loss'] * (opt['value'] ** decision_stress['punishment_sensitivity']))# 添加选项偏好的个体差异if i == 3:  # 确定收益选项utility *= (1 + 0.2 * decision_stress['risk_aversion'])expected_utilities.append(utility)# 添加随机噪声noise = np.random.normal(0, 0.08 * (1 + stress_level))expected_utilities = [eu + noise for eu in expected_utilities]# 压力诱导的选择偏差if np.random.random() < decision_stress['habit_bias']:# 习惯性选择 - 偏好确定性或熟悉选项choice = 3  # 确定收益选项else:# 审慎选择 - 基于期望效用choice = np.argmax(expected_utilities)# 模拟反应时 - 压力影响决策速度base_rt = 800 + np.random.normal(0, 150)  # 毫秒stress_rt_effect = 200 * stress_level * (1 - brain_stress['dlPFC'])reaction_time = max(300, base_rt + stress_rt_effect)# 模拟结果chosen_opt = options[choice]if np.random.random() < chosen_opt['prob_win']:outcome = chosen_opt['value']else:outcome = -chosen_opt['value'] * 0.6  # 损失厌恶系数choices.append(choice)outcomes.append(outcome)reaction_times.append(reaction_time)expected_utilities_history.append(expected_utilities.copy())return choices, outcomes, reaction_times, options, expected_utilities_historydef iowa_gambling_task(self, stress_level, trials=100, individual_vulnerability=0.5):"""爱荷华赌博任务 - 基于Bechara et al. (1994)的范式"""decks = {'A': {'win': 100, 'loss_prob': 0.5, 'loss_amount': 150, 'net': -25, 'label': 'A(不利)'},'B': {'win': 100, 'loss_prob': 0.1, 'loss_amount': 1250, 'net': -25, 'label': 'B(不利)'},'C': {'win': 50, 'loss_prob': 0.5, 'loss_amount': 50, 'net': 0, 'label': 'C(有利)'},'D': {'win': 50, 'loss_prob': 0.1, 'loss_amount': 250, 'net': 25, 'label': 'D(有利)'}}brain_stress, decision_stress, _ = self.apply_stress(stress_level, 1.0, individual_vulnerability)choices = []cumulative_earnings = 0earnings_history = []deck_preferences = {deck: 0 for deck in decks}deck_experiences = {deck: [] for deck in decks}for trial in range(trials):# 强化学习模型 - 基于经验的价值更新deck_values = {}for deck in decks:# 基于过往经验experiences = deck_experiences[deck]if experiences:exp_value = np.mean(experiences[-10:])  # 最近10次经验else:exp_value = 0# 结合基础偏好和学习deck_values[deck] = (exp_value +deck_preferences[deck] * 0.1 +np.random.normal(0, 0.05))# 压力影响探索-利用权衡exploration_rate = 0.3 - 0.25 * stress_level  # 压力降低探索if np.random.random() < exploration_rate and trial > 20:# 探索阶段 - 随机选择未充分探索的牌组under_explored = [d for d in decks if deck_preferences[d] < trial / 10]if under_explored:choice = np.random.choice(under_explored)else:choice = max(deck_values, key=deck_values.get)else:# 利用阶段 - 基于价值选择choice = max(deck_values, key=deck_values.get)# 模拟抽牌结果deck = decks[choice]win = deck['win']loss = 0if np.random.random() < deck['loss_prob']:loss = -deck['loss_amount']trial_earning = win + losscumulative_earnings += trial_earning# 更新学习模型deck_experiences[choice].append(trial_earning)if len(deck_experiences[choice]) > 20:deck_experiences[choice].pop(0)choices.append(choice)earnings_history.append(cumulative_earnings)deck_preferences[choice] += 1return choices, earnings_history, decksdef risk_decision_task(self, stress_level, trials=50, individual_vulnerability=0.5):"""风险决策任务 - 基于Kahneman & Tversky的前景理论范式"""scenarios = [{'certain': 40, 'risky': [(0.8, 50), (0.2, 0)], 'domain': 'gain', 'label': '风险规避测试'},{'certain': -30, 'risky': [(0.5, 0), (0.5, -50)], 'domain': 'loss', 'label': '损失规避测试'},{'certain': 20, 'risky': [(0.9, 100), (0.1, 0)], 'domain': 'gain', 'label': '高收益风险测试'},{'certain': -40, 'risky': [(0.3, 0), (0.7, -100)], 'domain': 'loss', 'label': '高损失风险测试'}]brain_stress, decision_stress, _ = self.apply_stress(stress_level, 1.0, individual_vulnerability)choices = []  # True选择风险选项，False选择确定选项outcomes = []certainty_equivalents = []for trial in range(trials):scenario = scenarios[trial % len(scenarios)]# 前景理论价值计算def prospect_value(amount, probability, domain):"""基于前景理论的价值函数"""alpha = 0.88  # 收益域风险规避参数beta = 0.92  # 损失域风险寻求参数lambda_val = 2.25  # 损失厌恶系数if domain == 'gain':if amount >= 0:return probability * (amount ** alpha)else:return probability * (-lambda_val * ((-amount) ** beta))else:  # loss domainif amount <= 0:return probability * (-lambda_val * ((-amount) ** beta))else:return probability * (amount ** alpha)# 计算确定选项价值certain_value = prospect_value(scenario['certain'], 1.0, scenario['domain'])# 计算风险选项期望价值risky_value = 0for prob, amount in scenario['risky']:risky_value += prospect_value(amount, prob, scenario['domain'])# 压力影响决策阈值risk_threshold = 0.5 - 0.4 * stress_level * individual_vulnerability# 做出选择if risky_value - certain_value > risk_threshold:choice = True  # 选择风险选项# 根据概率分布选择结果rand_val = np.random.random()cum_prob = 0outcome = 0for prob, amount in scenario['risky']:cum_prob += probif rand_val <= cum_prob:outcome = amountbreakelse:choice = False  # 选择确定选项outcome = scenario['certain']choices.append(choice)outcomes.append(outcome)# 计算确定性等价certainty_equivalent = certain_value + (risky_value - certain_value) * 0.5certainty_equivalents.append(certainty_equivalent)return choices, outcomes, scenarios, certainty_equivalentsdef plot_neural_activity_heatmap(brain_baseline, brain_stress):"""绘制脑区活动热图"""fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))regions = list(brain_baseline.keys())baseline_values = [brain_baseline[r] for r in regions]stress_values = [brain_stress[r] for r in regions]# 基准状态热图im1 = ax1.imshow([baseline_values], cmap='RdYlBu_r', aspect='auto', vmin=0, vmax=1)ax1.set_xticks(range(len(regions)))ax1.set_xticklabels(regions, rotation=45, ha='right')ax1.set_yticks([0])ax1.set_yticklabels(['基准状态'])ax1.set_title('基准状态脑区活动水平')plt.colorbar(im1, ax=ax1)# 压力状态热图im2 = ax2.imshow([stress_values], cmap='RdYlBu_r', aspect='auto', vmin=0, vmax=1)ax2.set_xticks(range(len(regions)))ax2.set_xticklabels(regions, rotation=45, ha='right')ax2.set_yticks([0])ax2.set_yticklabels(['压力状态'])ax2.set_title('压力下脑区活动水平')plt.colorbar(im2, ax=ax2)plt.tight_layout()return figdef plot_decision_parameters_radar(decision_baseline, decision_stress):"""绘制决策参数雷达图"""categories = list(decision_baseline.keys())N = len(categories)angles = [n / float(N) * 2 * np.pi for n in range(N)]angles += angles[:1]baseline_values = list(decision_baseline.values())stress_values = list(decision_stress.values())baseline_values += baseline_values[:1]stress_values += stress_values[:1]fig, ax = plt.subplots(figsize=(8, 8), subplot_kw=dict(projection='polar'))ax.plot(angles, baseline_values, 'o-', linewidth=2, label='基准状态', color='blue')ax.fill(angles, baseline_values, alpha=0.25, color='blue')ax.plot(angles, stress_values, 'o-', linewidth=2, label='压力状态', color='red')ax.fill(angles, stress_values, alpha=0.25, color='red')ax.set_xticks(angles[:-1])ax.set_xticklabels(categories, fontsize=9)ax.set_ylim(0, 1)ax.legend(loc='upper right', bbox_to_anchor=(1.3, 1.0))ax.set_title('决策参数变化雷达图', size=14, fontweight='bold')ax.grid(True)return figdef plot_neurotransmitter_changes(neuro_baseline, neuro_stress):"""绘制神经递质变化图"""neurotransmitters = list(neuro_baseline.keys())baseline_values = [neuro_baseline[nt] for nt in neurotransmitters]stress_values = [neuro_stress[nt] for nt in neurotransmitters]# 标准化处理以便在同一图中显示baseline_norm = [v / max(baseline_values) for v in baseline_values]stress_norm = [v / max(stress_values) for v in stress_values]fig, ax = plt.subplots(figsize=(10, 6))x = np.arange(len(neurotransmitters))width = 0.35bars1 = ax.bar(x - width / 2, baseline_norm, width, label='基准水平', alpha=0.7, color='lightblue')bars2 = ax.bar(x + width / 2, stress_norm, width, label='压力水平', alpha=0.7, color='salmon')ax.set_xlabel('神经递质')ax.set_ylabel('相对水平 (标准化)')ax.set_title('压力对神经递质水平的影响')ax.set_xticks(x)ax.set_xticklabels(neurotransmitters)ax.legend()# 添加数值标签for i, (b1, b2) in enumerate(zip(bars1, bars2)):ax.text(b1.get_x() + b1.get_width() / 2., b1.get_height() + 0.01,f'{baseline_values[i]:.1f}', ha='center', va='bottom', fontsize=8)ax.text(b2.get_x() + b2.get_width() / 2., b2.get_height() + 0.01,f'{stress_values[i]:.1f}', ha='center', va='bottom', fontsize=8)plt.tight_layout()return figdef plot_task_performance_comparison(stress_levels, performance_metrics, task_name):"""绘制任务性能随压力变化图"""fig, axes = plt.subplots(2, 2, figsize=(12, 8))axes = axes.ravel()metrics = list(performance_metrics.keys())for i, metric in enumerate(metrics):if i < 4:  # 只绘制前4个指标values = performance_metrics[metric]axes[i].plot(stress_levels, values, 'o-', linewidth=2, markersize=6)axes[i].set_xlabel('压力水平')axes[i].set_ylabel(metric)axes[i].set_title(f'{metric} vs 压力水平')axes[i].grid(True, alpha=0.3)# 添加趋势线if len(stress_levels) > 1:z = np.polyfit(stress_levels, values, 2)p = np.poly1d(z)stress_continuous = np.linspace(min(stress_levels), max(stress_levels), 100)axes[i].plot(stress_continuous, p(stress_continuous), '--', alpha=0.7, color='red')plt.tight_layout()return figdef main():st.set_page_config(page_title="SIDI模型压力决策模拟系统",page_icon="🧠",layout="wide",initial_sidebar_state="expanded")# 设置中文字体try:plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']plt.rcParams['axes.unicode_minus'] = Falseexcept:passst.title("🧠 SIDI模型：压力诱导的审慎到直觉决策模拟系统")st.markdown("""### Stress-induced Deliberation-to-Intuition (SIDI) Model基于Yu (2016)的神经计算模型，模拟急性压力如何通过影响大脑活动导致决策偏差""")# 侧边栏控制st.sidebar.header("🔧 模拟参数设置")col1, col2 = st.sidebar.columns(2)with col1:stress_level = st.slider("压力水平", 0.0, 1.0, 0.5, 0.01,help="0: 无压力, 1: 极高压力")with col2:vulnerability = st.slider("个体易感性", 0.0, 1.0, 0.5, 0.01,help="个体对压力的敏感程度")task_type = st.sidebar.selectbox("决策任务类型",["概率选择任务", "爱荷华赌博任务", "风险决策任务"])num_trials = st.sidebar.slider("试验次数", 20, 200, 100)# 高级参数with st.sidebar.expander("🧬 高级神经参数"):stress_duration = st.slider("压力持续时间(小时)", 0.5, 8.0, 1.0, 0.5)show_neurotransmitters = st.checkbox("显示神经递质数据")show_individual_diff = st.checkbox("显示个体差异分析")# 初始化模型model = SIDIModel()# 主显示区域st.header("🧬 神经生物学基础")# 计算压力影响brain_baseline = model.brain_regionsdecision_baseline = model.decision_paramsneuro_baseline = model.neurotransmittersbrain_stress, decision_stress, neuro_stress = model.apply_stress(stress_level, stress_duration, vulnerability)# 第一行：脑区活动和决策参数col1, col2 = st.columns(2)with col1:st.subheader("🏗️ 脑区活动变化")fig_brain = plot_neural_activity_heatmap(brain_baseline, brain_stress)st.pyplot(fig_brain)# 脑区变化数据表brain_df = pd.DataFrame({'脑区': list(brain_baseline.keys()),'基准活动': [f"{brain_baseline[r]:.3f}" for r in brain_baseline],'压力下活动': [f"{brain_stress[r]:.3f}" for r in brain_baseline],'变化率': [f"{(brain_stress[r] - brain_baseline[r]) / brain_baseline[r] * 100:+.1f}%"for r in brain_baseline]})st.dataframe(brain_df, use_container_width=True)with col2:st.subheader("📊 决策参数变化")fig_decision = plot_decision_parameters_radar(decision_baseline, decision_stress)st.pyplot(fig_decision)# 决策参数数据表decision_df = pd.DataFrame({'参数': list(decision_baseline.keys()),'基准值': [f"{decision_baseline[r]:.3f}" for r in decision_baseline],'压力下值': [f"{decision_stress[r]:.3f}" for r in decision_baseline],'变化方向': ['↓' if decision_stress[r] < decision_baseline[r] else '↑'for r in decision_baseline]})st.dataframe(decision_df, use_container_width=True)# 神经递质变化if show_neurotransmitters:st.subheader("🧪 神经内分泌变化")fig_neuro = plot_neurotransmitter_changes(neuro_baseline, neuro_stress)st.pyplot(fig_neuro)neuro_df = pd.DataFrame({'神经递质': list(neuro_baseline.keys()),'基准水平': [f"{neuro_baseline[nt]:.1f}" for nt in neuro_baseline],'压力下水平': [f"{neuro_stress[nt]:.1f}" for nt in neuro_baseline],'变化百分比': [f"{(neuro_stress[nt] - neuro_baseline[nt]) / neuro_baseline[nt] * 100:+.1f}%"for nt in neuro_baseline]})st.dataframe(neuro_df, use_container_width=True)# 决策任务模拟st.header("🎯 决策任务模拟")# 根据选择的任务运行模拟if task_type == "概率选择任务":with st.spinner('正在进行概率选择任务模拟...'):choices, outcomes, reaction_times, options, expected_utilities = \model.probabilistic_selection_task(stress_level, num_trials, vulnerability)# 显示结果col1, col2 = st.columns(2)with col1:# 选择分布choice_counts = pd.Series(choices).value_counts().sort_index()fig, ax = plt.subplots(figsize=(10, 6))bars = ax.bar(range(len(choice_counts)), choice_counts.values,color=['red', 'orange', 'yellow', 'green'], alpha=0.7)ax.set_xlabel('选项')ax.set_ylabel('选择次数')ax.set_title('选项选择分布')ax.set_xticks(range(len(choice_counts)))ax.set_xticklabels([f'选项{i + 1}' for i in range(len(choice_counts))])for bar in bars:height = bar.get_height()ax.text(bar.get_x() + bar.get_width() / 2., height,f'{int(height)}', ha='center', va='bottom')st.pyplot(fig)with col2:# 收益累积cumulative_outcomes = np.cumsum(outcomes)fig, ax = plt.subplots(figsize=(10, 6))ax.plot(cumulative_outcomes, linewidth=2, color='blue')ax.set_xlabel('试验次数')ax.set_ylabel('累计收益')ax.set_title('收益累积曲线')ax.grid(True, alpha=0.3)ax.axhline(y=0, color='red', linestyle='--', alpha=0.5)st.pyplot(fig)# 性能指标total_earnings = sum(outcomes)risk_taking = len([c for c in choices if c in [0, 1]]) / len(choices)avg_reaction_time = np.mean(reaction_times)col3, col4, col5 = st.columns(3)col3.metric("总收益", f"{total_earnings:.1f}")col4.metric("风险选择比例", f"{risk_taking * 100:.1f}%")col5.metric("平均反应时(ms)", f"{avg_reaction_time:.0f}")elif task_type == "爱荷华赌博任务":with st.spinner('正在进行爱荷华赌博任务模拟...'):choices, earnings, decks = model.iowa_gambling_task(stress_level, num_trials, vulnerability)# 显示结果col1, col2 = st.columns(2)with col1:# 牌组选择序列fig, ax = plt.subplots(figsize=(12, 6))choice_mapping = {'A': 0, 'B': 1, 'C': 2, 'D': 3}numeric_choices = [choice_mapping[c] for c in choices]# 使用散点图显示选择序列for i, choice in enumerate(numeric_choices):ax.scatter(i, choice, color=['red', 'orange', 'green', 'blue'][choice],alpha=0.6, s=30)ax.set_yticks([0, 1, 2, 3])ax.set_yticklabels(['A(不利)', 'B(不利)', 'C(有利)', 'D(有利)'])ax.set_xlabel('试验次数')ax.set_ylabel('选择的牌组')ax.set_title('牌组选择序列')ax.grid(True, alpha=0.3)st.pyplot(fig)with col2:# 收益累积fig, ax = plt.subplots(figsize=(10, 6))ax.plot(earnings, linewidth=2, color='green')ax.axhline(y=0, color='red', linestyle='--', alpha=0.5)ax.set_xlabel('试验次数')ax.set_ylabel('累计收益')ax.set_title('收益累积曲线')ax.grid(True, alpha=0.3)st.pyplot(fig)# 性能指标final_earnings = earnings[-1] if earnings else 0favorable_choices = len([c for c in choices if c in ['C', 'D']]) / len(choices)learning_slope = (earnings[-1] - earnings[0]) / len(earnings) if len(earnings) > 1 else 0col3, col4, col5 = st.columns(3)col3.metric("最终收益", f"{final_earnings:.1f}")col4.metric("有利牌组选择", f"{favorable_choices * 100:.1f}%")col5.metric("学习斜率", f"{learning_slope:.2f}")else:  # 风险决策任务with st.spinner('正在进行风险决策任务模拟...'):choices, outcomes, scenarios, certainty_equivalents = \model.risk_decision_task(stress_level, num_trials, vulnerability)# 显示结果col1, col2 = st.columns(2)with col1:# 风险选择比例risk_choices = sum(choices)certain_choices = len(choices) - risk_choicesfig, ax = plt.subplots(figsize=(8, 6))ax.pie([risk_choices, certain_choices],labels=['风险选择', '确定选择'],autopct='%1.1f%%', colors=['lightcoral', 'lightblue'])ax.set_title('风险选择比例')st.pyplot(fig)with col2:# 收益分布fig, ax = plt.subplots(figsize=(10, 6))ax.hist(outcomes, bins=15, alpha=0.7, color='purple', edgecolor='black')ax.set_xlabel('收益值')ax.set_ylabel('频次')ax.set_title('收益分布直方图')ax.grid(True, alpha=0.3)st.pyplot(fig)# 性能指标risk_choice_ratio = sum(choices) / len(choices)avg_outcome = np.mean(outcomes)outcome_variance = np.std(outcomes)col3, col4, col5 = st.columns(3)col3.metric("风险选择比例", f"{risk_choice_ratio * 100:.1f}%")col4.metric("平均收益", f"{avg_outcome:.1f}")col5.metric("收益波动", f"{outcome_variance:.2f}")# 压力影响分析st.header("📈 压力影响分析")# 模拟不同压力水平下的性能stress_levels = np.linspace(0, 1, 6)performance_data = {'总收益': [],'风险选择比例': [],'认知控制效率': [],'习惯偏差': []}for sl in stress_levels:# 简化模拟用于趋势分析_, decision_temp, _ = model.apply_stress(sl, 1.0, vulnerability)performance_data['总收益'].append(100 * (1 - sl * 0.6))performance_data['风险选择比例'].append(0.6 - sl * 0.3)performance_data['认知控制效率'].append(decision_temp['cognitive_control'])performance_data['习惯偏差'].append(decision_temp['habit_bias'])fig_trend = plot_task_performance_comparison(stress_levels, performance_data, task_type)st.pyplot(fig_trend)# 理论框架with st.expander("📚 SIDI模型理论框架"):st.markdown("""### 压力诱导的审慎到直觉转换 (SIDI模型)**核心神经机制：**- **前额叶皮层抑制**: 压力激素(皮质醇)削弱执行控制功能- **杏仁核-脑岛激活**: 增强威胁检测和情绪反应- **纹状体功能改变**: 奖赏处理系统重组- **网络连接重组**: 从执行控制网络转向突显网络主导**决策偏差模式：**1. **奖赏敏感性降低**: 对积极结果的反应减弱2. **惩罚敏感性增强**: 对负面结果的过度反应  3. **风险偏好改变**: 复杂的非线性U型变化4. **习惯偏差增加**: 自动化反应替代理性分析5. **框架效应增强**: 更易受问题表述方式影响**计算神经科学基础：**- 基于强化学习模型的价值更新机制- 前景理论的风险决策框架- 双系统理论的认知架构""")# 参考文献with st.expander("📖 参考文献与实证依据"):st.markdown("""**主要理论依据：**- Yu, R. (2016). Stress potentiates decision biases: A stress induced deliberation-to-intuition (SIDI) model. *Neurobiology of Stress*- Arnsten, A. F. T. (2009). Stress signalling pathways that impair prefrontal cortex structure and function. *Nature Reviews Neuroscience*- Schwabe, L., & Wolf, O. T. (2011). Stress-induced modulation of instrumental learning. *Behavioural Brain Research*- Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. *Econometrica***神经影像学证据：**- fMRI显示压力下PFC-amygdala功能连接改变- PET研究证实压力激素对决策网络的调节作用- EEG研究揭示压力对决策过程的时间动力学影响""")if __name__ == "__main__":main()