MIT-最长公共子序列问题(LCS)
文章目录
- 问题描述
- 例子
- 算法实现
- 暴力算法
- 动态规划
问题描述
给定两个字符串(或序列)AAA 和 BBB,求它们的 最长公共子序列(Longest Common Subsequence, LCS) 的长度。且 length(A)=n,length(B)=mlength(A)=n,length(B)=mlength(A)=n,length(B)=m。
子序列(subsequence)指的是从一个序列中删除若干(可以为0个)元素后,不改变原有顺序而得到的新序列。
注意:子序列中的字符不要求连续。
例子
设
A = "ABCBDAB"
B = "BDCABA"
则它们的所有公共子序列包括:
"BCBA", "BDAB", "BCAB", "BDABA", "BCBAB" ...
其中最长的公共子序列长度是 4,
可能的 LCS 之一为:
"BCAB"
因此应该输出4。
算法实现
暴力算法
首先最直观的想法就是我们,可以列举出 AAA 字符串所有子序列一共 2n2^n2n 个子序列。
因为 len(A)=nlen(A)=nlen(A)=n,每一位都有“选”和“不选”两种。所以一共有 2n2^n2n 种排列方式。
然后对于 AAA 的 2n2^n2n 个所有子序列对 BBB 字符串进行匹配。最终得出最长公共子序列。
获取所有子序列
vector<string> getSubsequences(const string& str)
{vector<string> subsequences;int n = str.length();// 枚举从 0 到 (2^n - 1) 的所有数,表示包含/不包含某个字符for (int mask = 0; mask < (1 << n); mask++) {string subseq = "";for (int i = 0; i < n; i++) if (mask & (1 << i)) subseq += str[i]; // 如果第 i 位为 1,则包含该字符subsequences.push_back(subseq); // 把子序列加入列表}return subsequences;
}
判断 sub 是否为 str 的子序列
bool isSubsequence(const string& sub, const string& str)
{int i = 0, j = 0;while (i < sub.size() && j < str.size()) {if (sub[i] == str[j]) i ++ ;j ++ ;}return i == sub.size();
}
判断两个字符串的最长公共子序列
int LCSBySubsequences(string A, string B)
{vector<string> subsequencesA = getSubsequences(A);int maxLength = 0;for (const string& subseqA : subsequencesA)if (isSubsequence(subseqA , B))maxLength = max(maxLength, (int)subseqA.size());return maxLength;
}
时间复杂度:O(m2n)O(m2^n)O(m2n)
动态规划
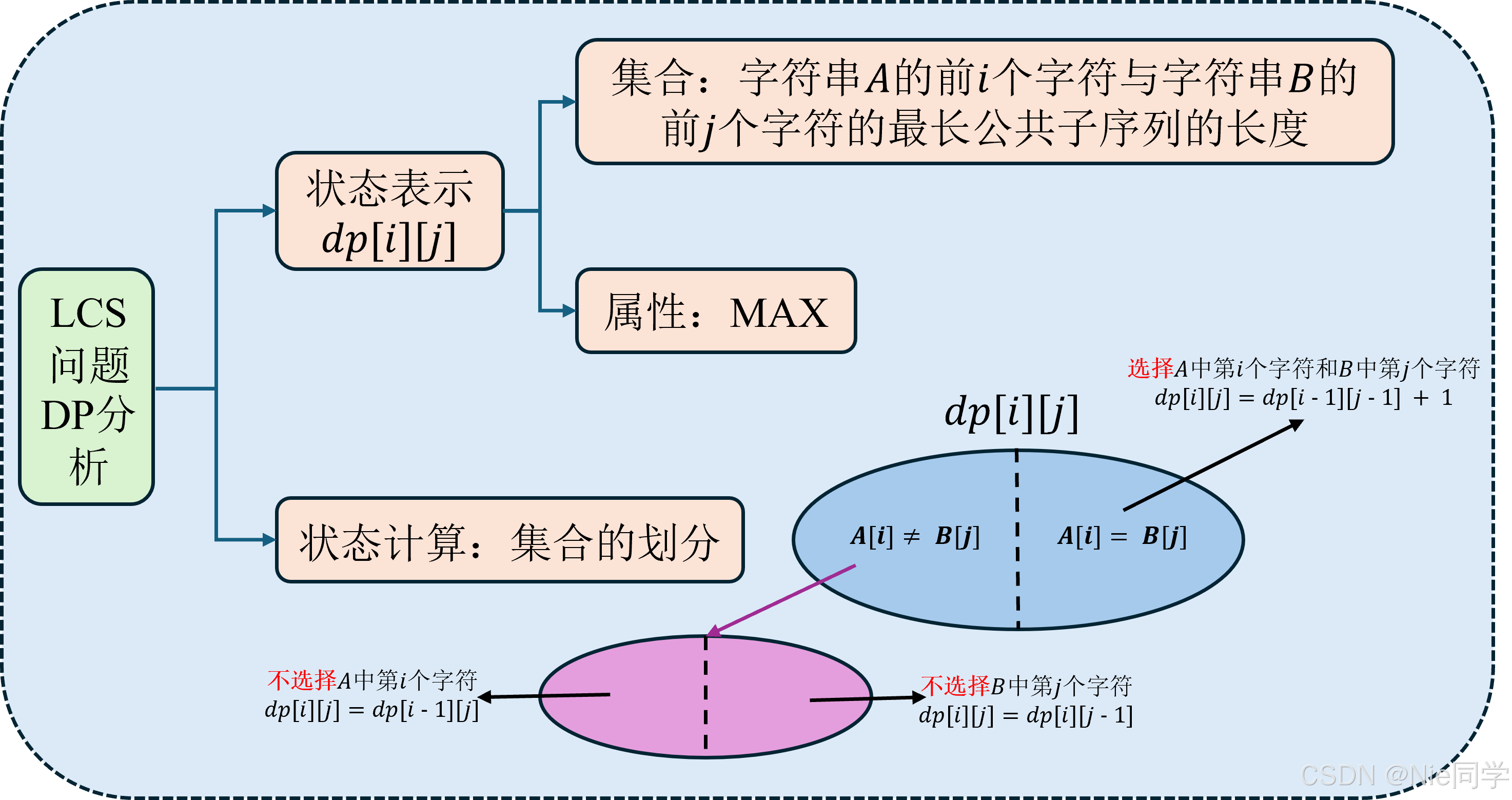
注:在A[i]≠B[j]A[i]\not=B[j]A[i]=B[j] 时为什么不能同时丢掉 AAA 中第 iii 个字符和 BBB 中第 jjj 个字符(dp[i][j]=dp[i−1][j−1]dp[i][j]=dp[i - 1][j - 1]dp[i][j]=dp[i−1][j−1])?
因为 “两个都丢掉” 的情况已经被包含在别的转移中 。dp[i−1][j−1]≤dp[i−1][j]dp[i-1][j-1]\leq dp[i-1][j]dp[i−1][j−1]≤dp[i−1][j] 且 dp[i−1][j−1]≤dp[i][j−1]dp[i-1][j-1]\leq dp[i][j-1]dp[i−1][j−1]≤dp[i][j−1]。
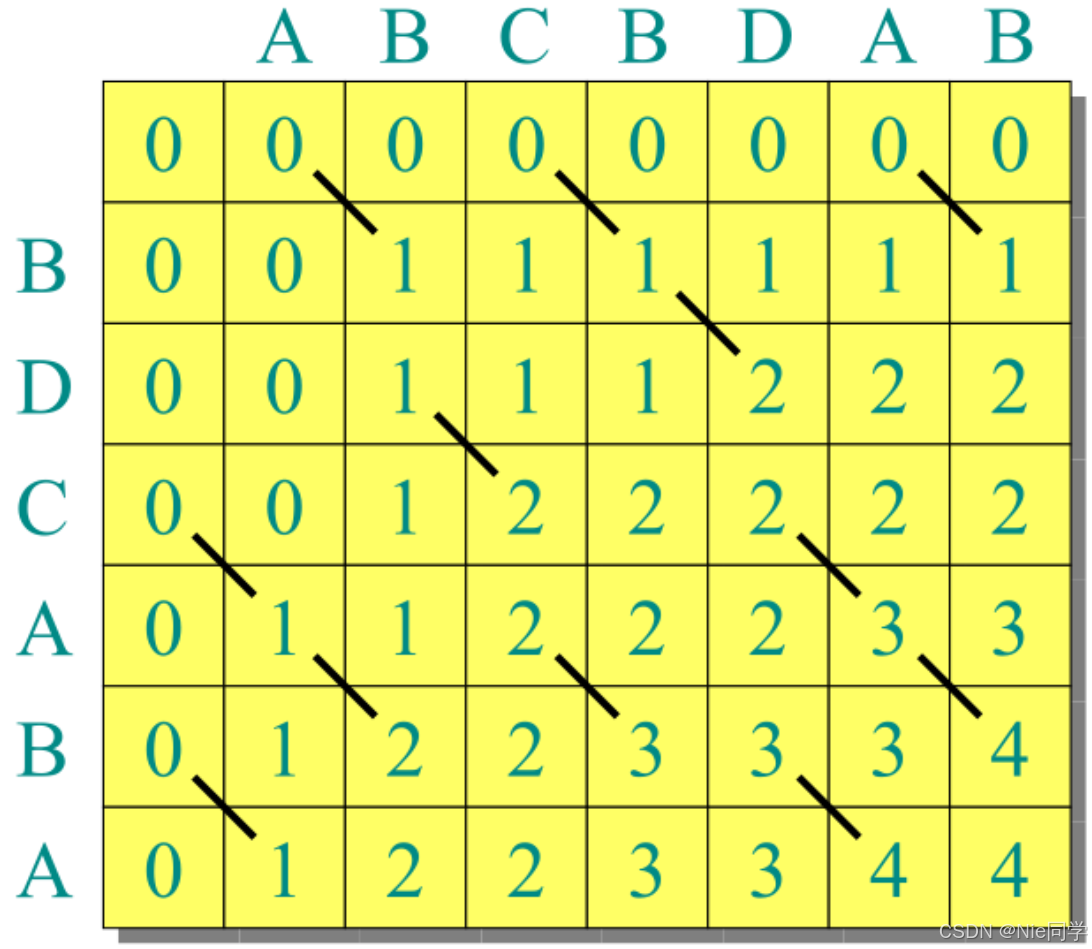
int dpLCS(String A, String B)
{int n = A.size(), m = B.size();int dp[n + 1][m + 1];for (int i = 0; i <= m; i ++ ) dp[0][i] = 0;for (int i = 0; i <= n; i ++ ) dp[i][0] = 0;for (int i = 1; i <= n; i ++ ){for (int j = 1; j <= m; j ++ ){if (A[i] == B[j])dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}return dp[n][m];
}
时间复杂度:O(nm)O(nm)O(nm)
