LeetCode - 杨辉三角 / 二叉树的最大深度
杨辉三角 / 二叉树的最大深度
欢迎光临小站:致橡树
杨辉三角
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
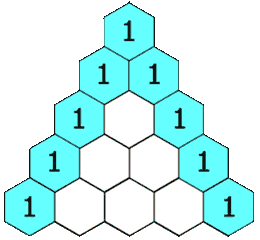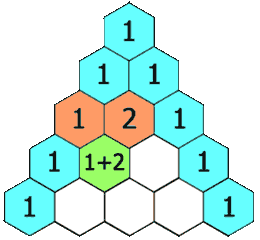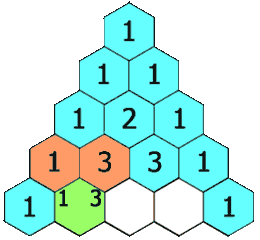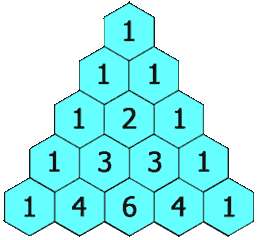
示例 1:
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1
输出: [[1]]
提示:
-
1 <= numRows <= 30
解题思路
这段代码是用于生成帕斯卡三角形(杨辉三角)的实现。给定一个非负整数 numRows,生成前 numRows 行的帕斯卡三角形。
代码逻辑
-
初始化:
-
创建一个
ArrayList来存储结果,每个元素是一个List<Integer>表示一行 -
n初始化为1,表示当前正在处理第1行
-
-
外层循环:
-
while (numRows > 0)控制生成的行数 -
每次循环处理一行,
numRows减1,直到为0
-
-
处理每一行:
-
创建一个新的
ArrayList来存储当前行的数字 -
内层
for循环填充当前行的每个元素:-
第一个和最后一个元素总是1(
i == 0和i == n-1的情况) -
中间元素等于上一行对应位置和前一个位置元素的和(
list.get(n-2).get(i-1) + list.get(n-2).get(i)) -
n-2是因为列表从0开始索引,而n从1开始计数
-
-
-
添加行并更新计数器:
-
将当前行添加到结果列表中
-
n++准备处理下一行 -
numRows--减少剩余要处理的行数
-
示例
以 numRows = 5 为例:
-
第1行 (n=1):
[1] -
第2行 (n=2):
[1, 1] -
第3行 (n=3):
[1, 2, 1](1+1=2) -
第4行 (n=4):
[1, 3, 3, 1](1+2=3, 2+1=3) -
第5行 (n=5):
[1, 4, 6, 4, 1](1+3=4, 3+3=6, 3+1=4)
class Solution {public List<List<Integer>> generate(int numRows) {ArrayList<List<Integer>> list = new ArrayList();int n = 1;while (numRows > 0) {List<Integer> temp = new ArrayList(n);for (int i = 0; i < n; i++) {if (i == 0) {temp.add(1);continue;}if (i == (n - 1)) {temp.add(1);continue;}int left = list.get(n - 2).get(i - 1);int right = list.get(n - 2).get(i);temp.add(left + right);}list.add(temp);n++;numRows--;}return list;}public static void main(String[] args) {Solution solution = new Solution();List<List<Integer>> generate = solution.generate(1);System.out.println(generate);}
}二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
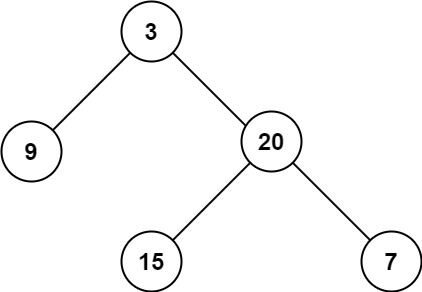
输入:root = [3,9,20,null,null,15,7]
输出:3
示例 2:
输入:root = [1,null,2]
输出:2
提示:
-
树中节点的数量在
[0, 104]区间内。 -
-100 <= Node.val <= 100
解题思路
递归遍历左右子树
这段代码是一个求二叉树最大深度的递归实现,我们按执行逻辑梳理一下:
-
递归结束条件(base case)
if (root == null) {return 0; }-
当当前节点为空,说明走到树的尽头(叶子节点的子节点),深度为 0
-
这是递归的出口,避免无限递归。
-
-
递归计算左子树深度
int left = maxDepth(root.left);-
对
root.left递归调用maxDepth -
直到走到空节点,才返回 0,然后逐层往上计算深度。
-
-
递归计算右子树深度
int right = maxDepth(root.right);-
同理,对右子树递归计算最大深度。
-
-
当前节点深度计算
return Math.max(left, right) + 1;-
左右子树深度取最大值
-
再加上当前节点本身的这一层深度(
+1) -
逐层返回给上一级调用。
-
class Solution {public int maxDepth(TreeNode root) {if (root == null) {return 0;}int left = maxDepth(root.left);int right = maxDepth(root.right);return Math.max(left, right) + 1;}
}广度遍历二叉树
采用广度优先搜索(BFS)的方法。下面是逐步逻辑分析:
-
基本情况处理
-
逻辑说明:如果根节点为空,说明树不存在,深度为 0。
-
if (root == null) {return 0;
}-
BFS 初始化
-
变量说明:
-
level:记录当前深度,初始为 0。 -
queue:创建一个队列,并将根节点加入队列,作为遍历的起点。
-
-
int level = 0;
LinkedList<TreeNode> queue = new LinkedList<>();
queue.add(root);-
BFS 主循环
-
外层循环:当队列不为空时,说明还有节点需要处理,循环继续。
-
内层循环:
-
目标:处理当前层的每一个节点。
-
步骤:
-
从队列中取出一个节点。
-
将其非空的左、右子节点加入队列末尾。
-
计数器
size减 1,表示已处理完当前层的一个节点。
-
-
当
size减至 0 时,表示当前层所有节点已处理完毕。
-
-
while (!queue.isEmpty()) { // 外层循环int size = queue.size(); // 获取当前层的节点数量while (size > 0) { // 内层循环:处理当前层的所有节点TreeNode poll = queue.poll(); // 取出队首节点// 将该节点的子节点加入队列,作为下一层待处理的节点if (poll.left != null) {queue.add(poll.left);}if (poll.right != null) {queue.add(poll.right);}size--; // 当前层节点计数器减 1}level++; // 完成一层处理后,深度加 1
}-
返回结果
-
逻辑说明:当队列为空时,表示所有节点都已处理完毕,返回累计的深度
level,即为树的最大深度。
-
return level;这种方法通过层级遍历的方式,每处理完一层深度加1,最终得到的level就是树的最大深度。
-
完整代码
class Solution {public int maxDepth(TreeNode root) {// 1. 基本情况处理if (root == null) {return 0;}// 2. BFS 初始化int level = 0;LinkedList<TreeNode> queue = new LinkedList<>();queue.add(root);// 3. BFS 主循环while (!queue.isEmpty()) {int size = queue.size(); // 获取当前层的节点数量// 处理当前层的所有节点while (size > 0) {TreeNode currentNode = queue.poll(); // 取出队首节点// 将该节点的子节点加入队列,作为下一层待处理的节点if (currentNode.left != null) {queue.add(currentNode.left);}if (currentNode.right != null) {queue.add(currentNode.right);}size--; // 当前层节点计数器减1}level++; // 完成一层处理后,深度加1}// 4. 返回结果return level;}
}