考研408--组成原理--day2--进制定点数符号拓展

（以下内容全部来自上述课程）

进位计数制

1. 最古老的计数方法

人类最开始计数是直接一个竖线表示1，但是数量越多，也不可能都用一个竖线挨个儿表示，所以演变成用符号表示权重的方式。
比如8个苹果，一个竖线表示一个，一个横线表示五个，所以就可以用三个竖线、一个横线表示八个苹果。
这里的权重（其实就是比例），横线：个数=1：5。
再到最后，就演变成了我们熟知的英文字符和阿拉伯数字。

2. 十进制计数法

就是我们小时候用手查数，刚好数到十，自己的两只手不够用了，就需要再加一只手。
我们用自己的手表示十之后，就可以用下一个人的手的一，表示我们所表示的十，这就是逢十进一。

推广：

3. 进制转换

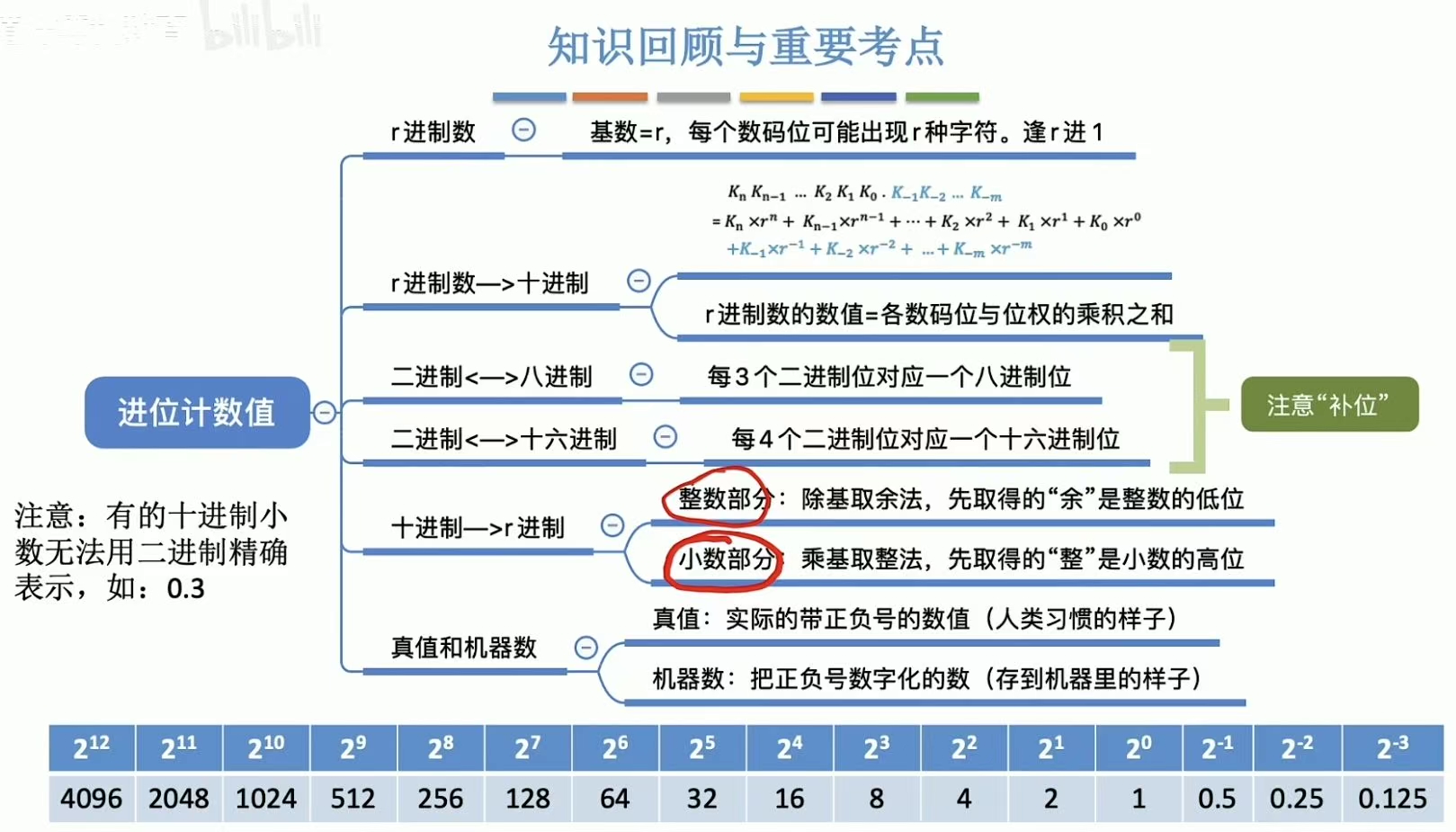
3.1 其他进制–>十进制

简单记：X进制数=此位本身*X^（本位-1）的和
嗯…还是直接看例题更好记一点儿

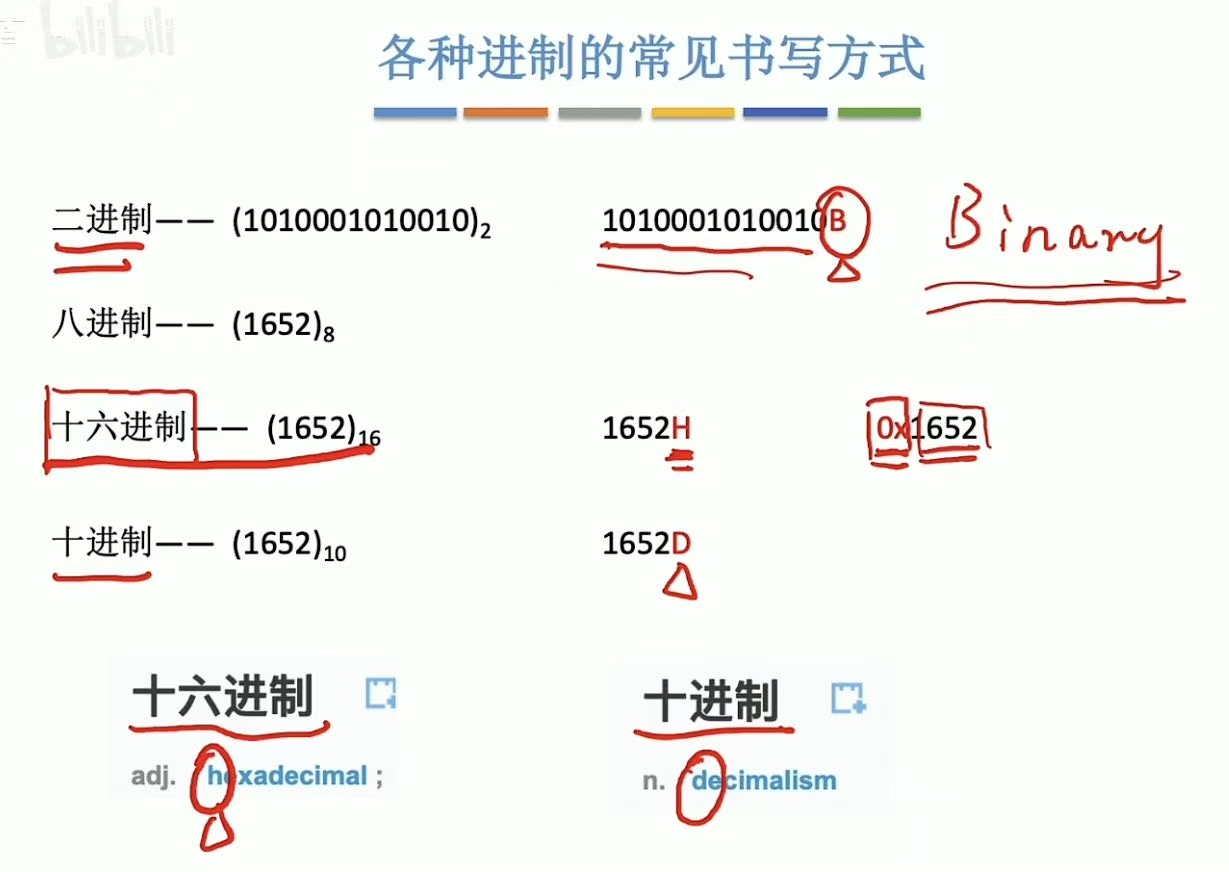
3.2 二进制<–>八进制、十六进制

2^3=8，所以可以三位三位分，直接转换。
2^4=16，所以可以四位四位分，直接转换。

各种进制的常见书写方式：

3.3 十进制–>任意进制

转换成几进制，就除以几。

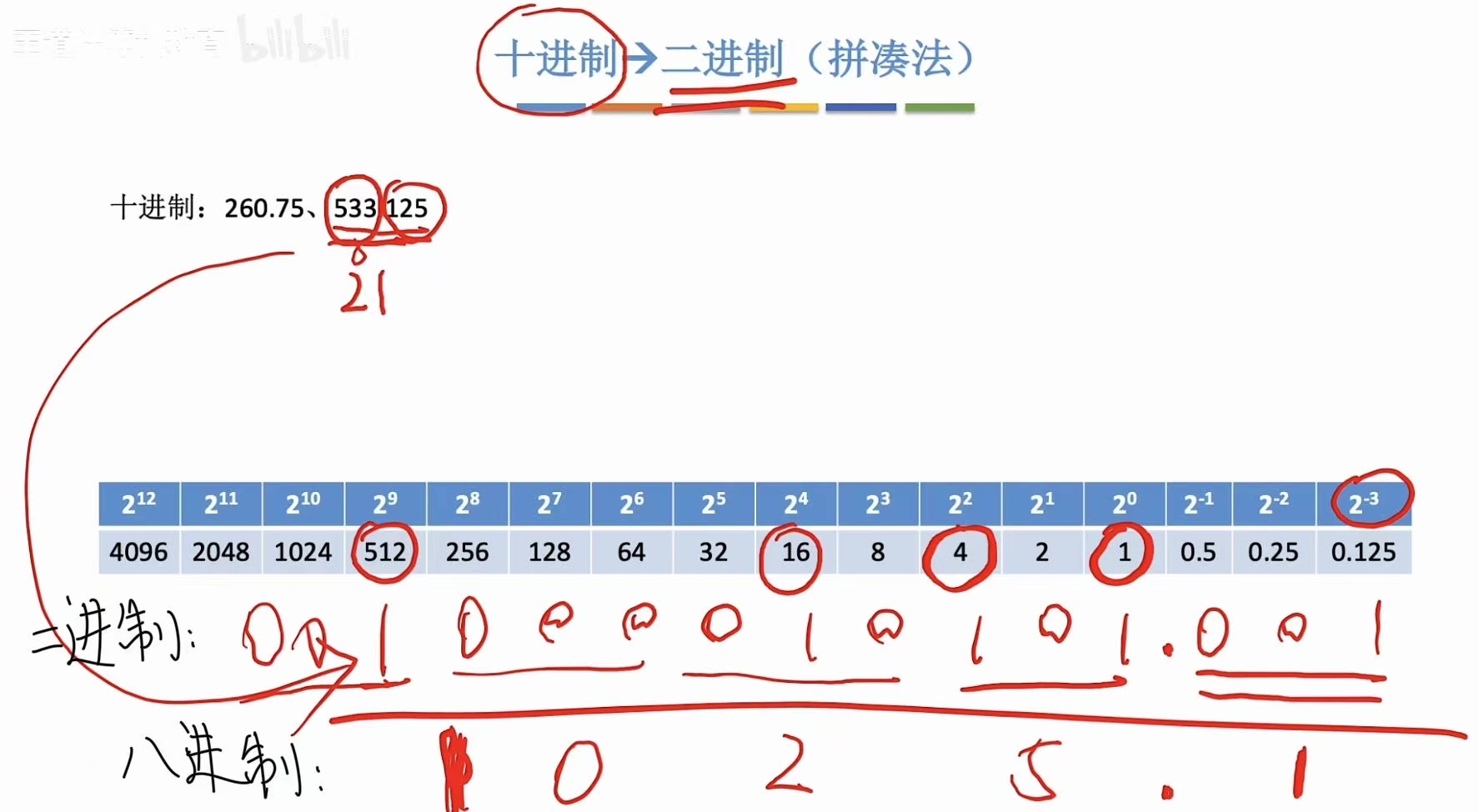
3.4 十进制–>二进制（拼凑法）

就是记住哪位的1表示的是十进制的多少，不够的话继续往下位看，可以加的位数就是1，不能的话就是0.
（语言叙述实在太麻烦了，建议听课会更好理解）

4. 真值&机器数

5. 小结

定点数的表示

1. 无符号数

通常只有无符号整数，没有无符号小数。

2. 有符号数

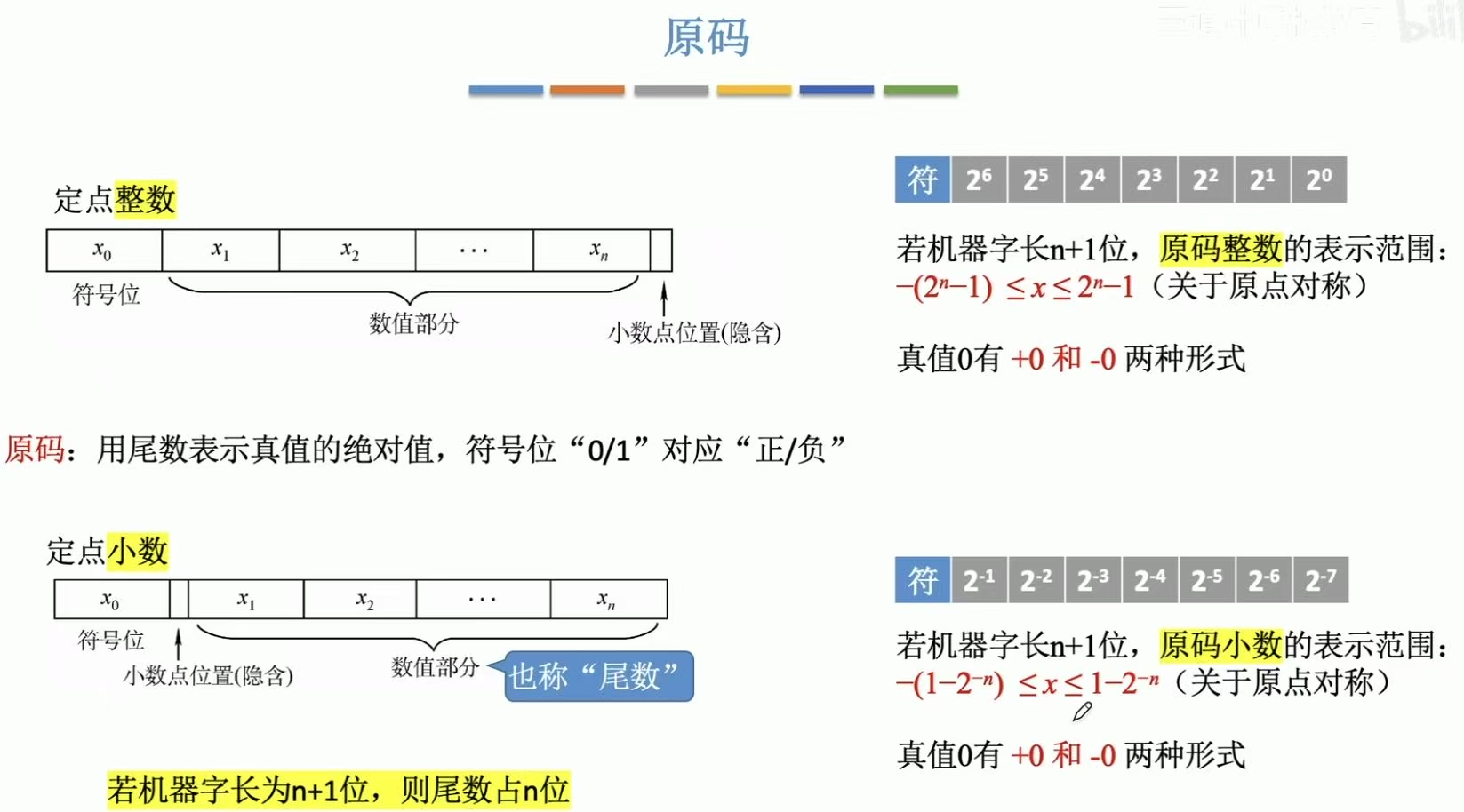
2.1 原码

定点整数：默认小数点位置在数值部分之后。
定点小数：默认小数点在符号位和数值部分之间。

0有两种形式。

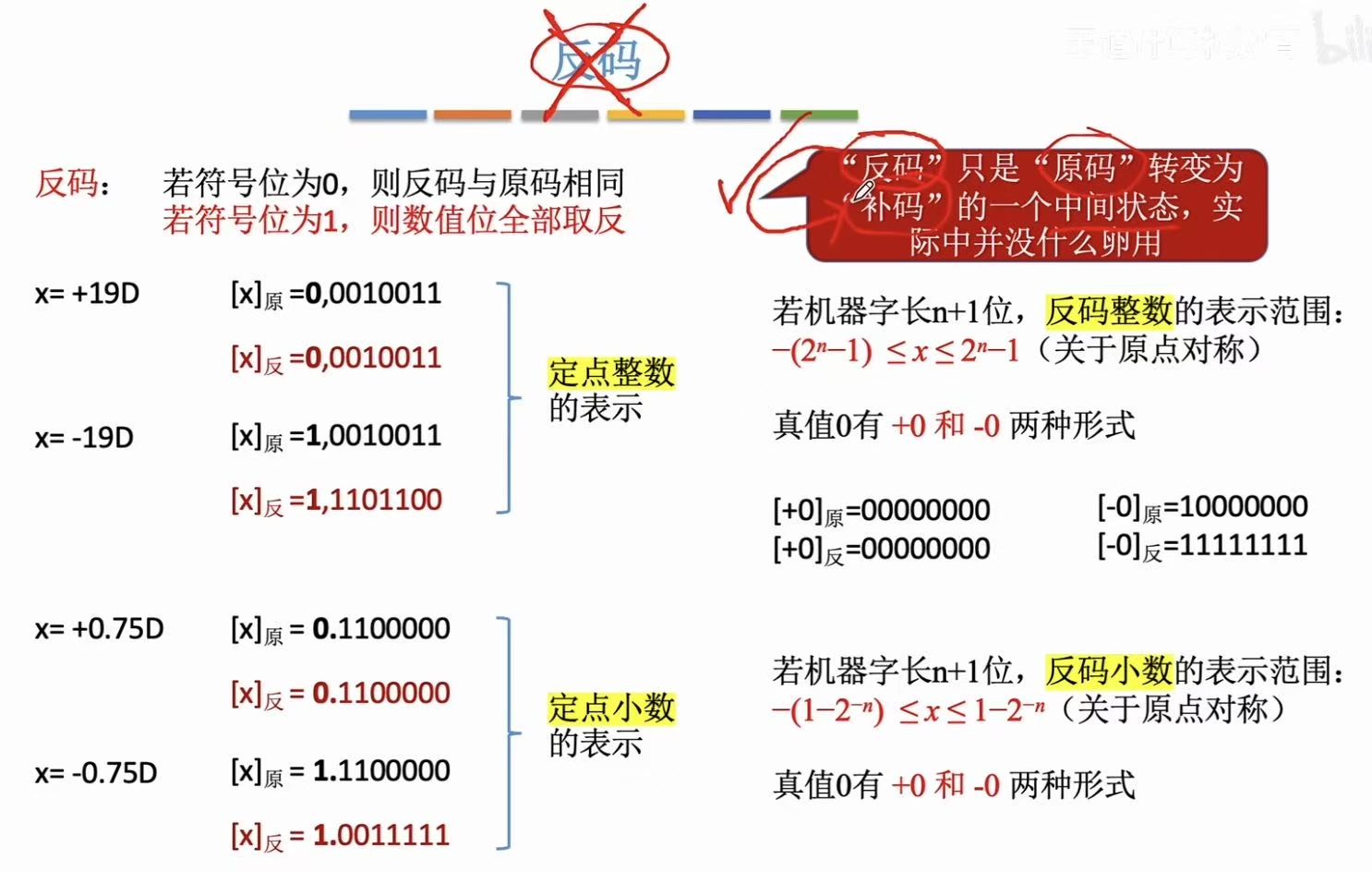
2.2 反码（无实际作用）

0有两种形式。

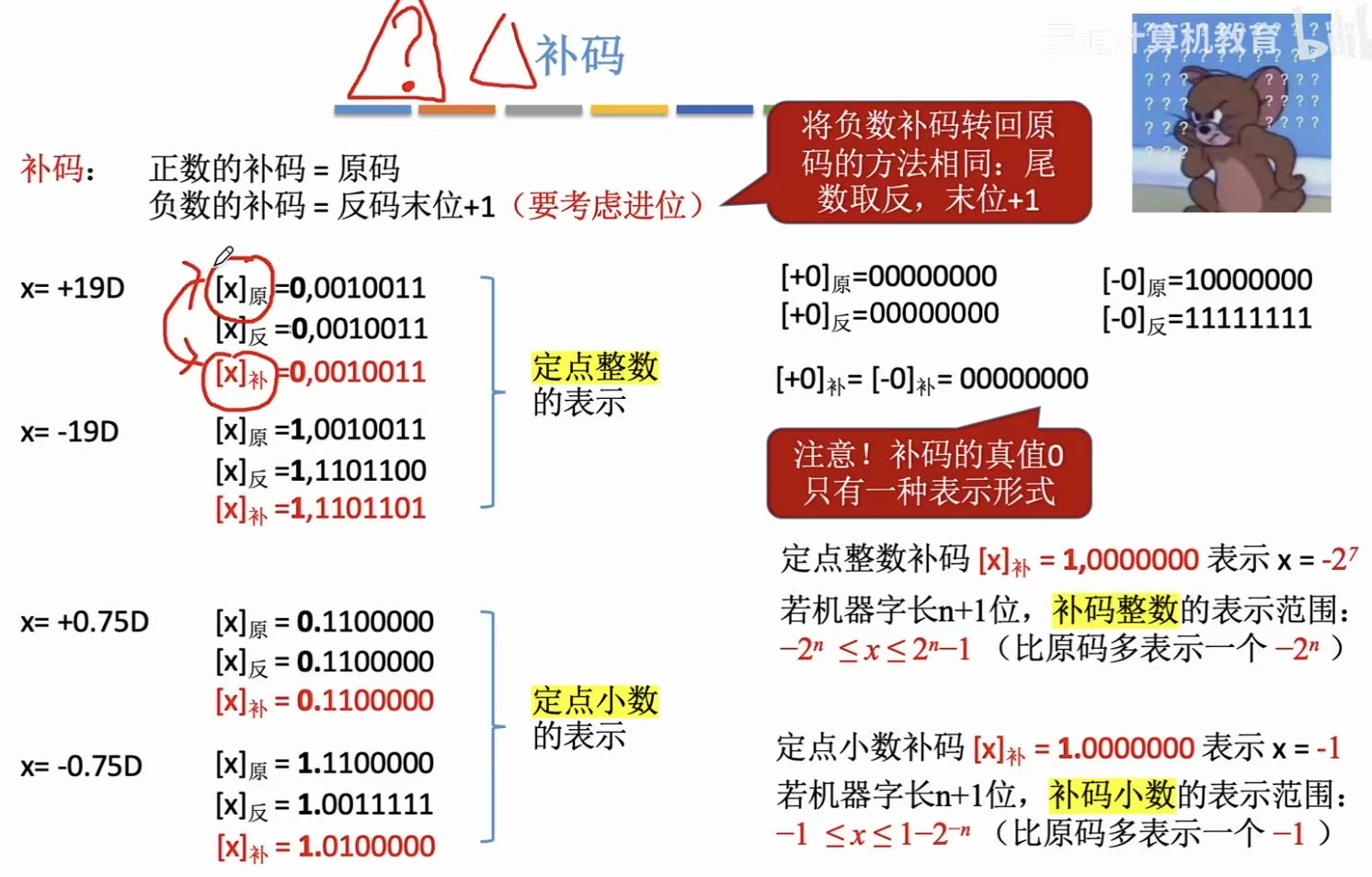
2.3 补码

0有一种形式，方便计算。

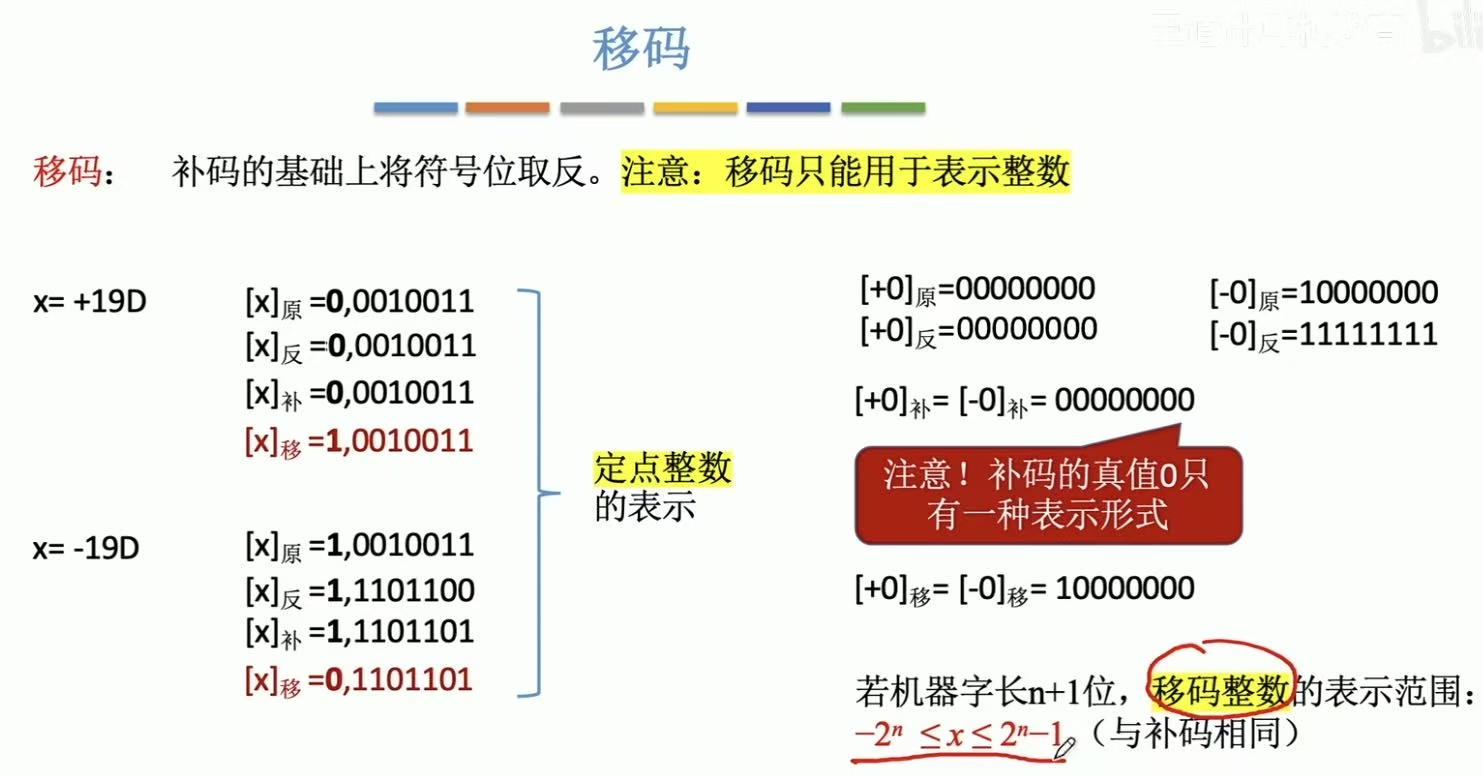
2.4 移码

0有一种形式。
只能用来表示整数。

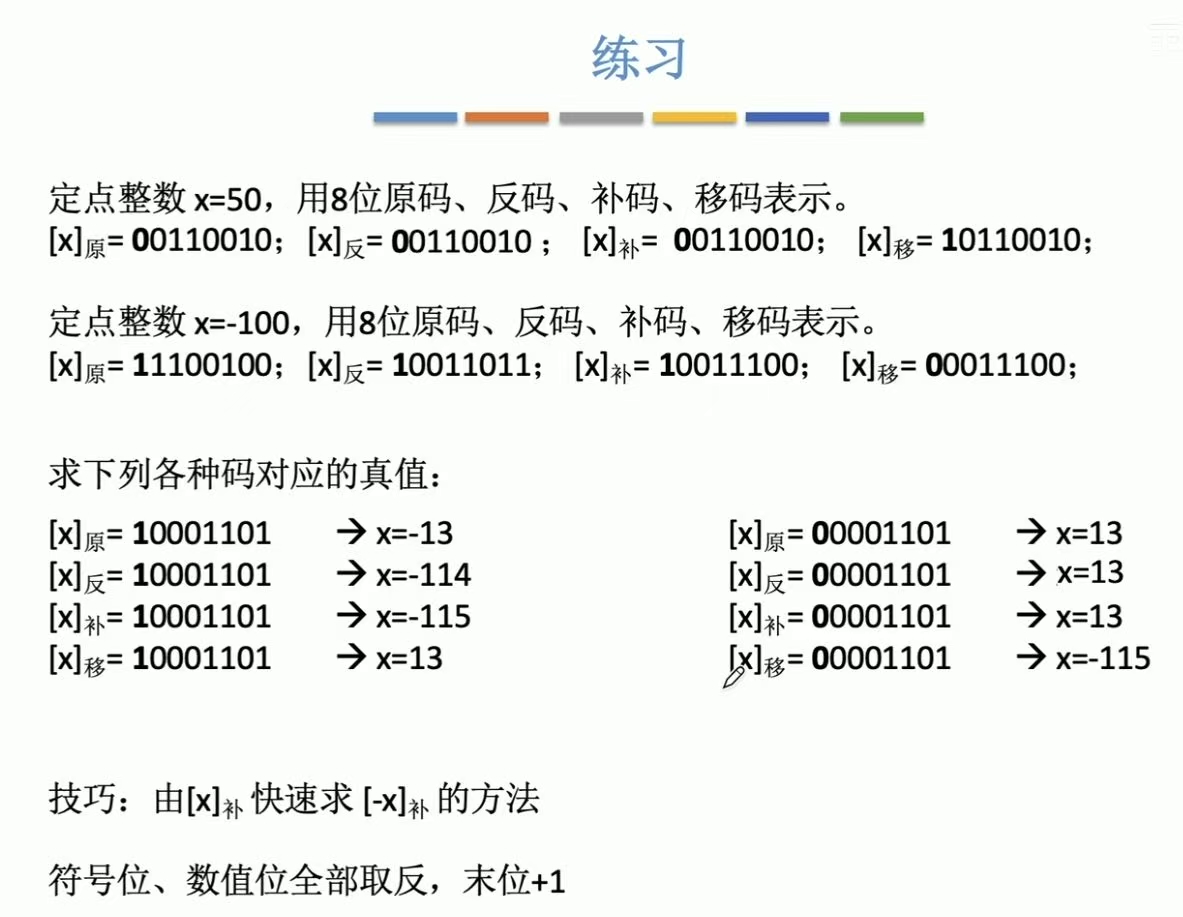
2.5 用几种码表示定点整数

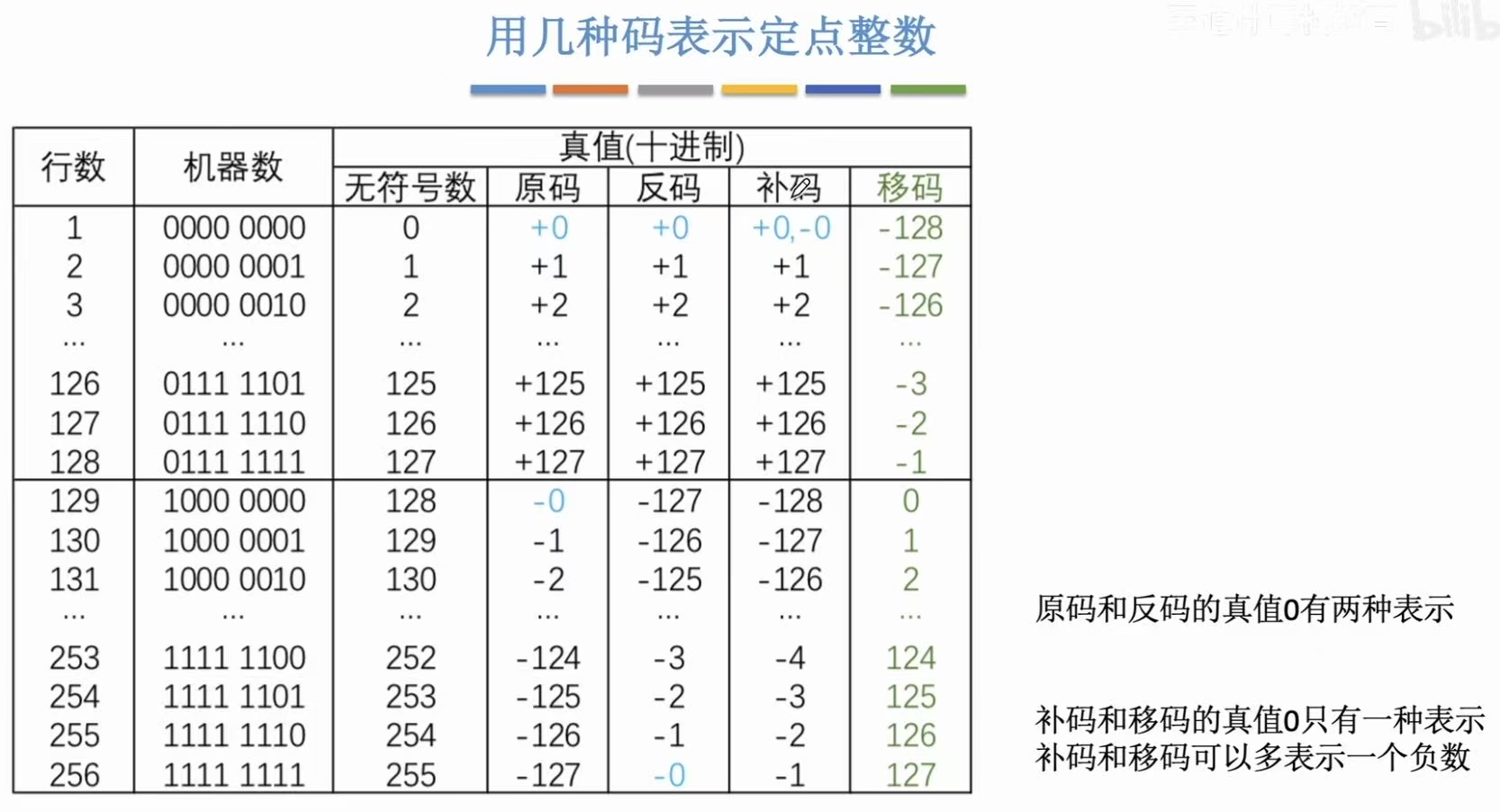
练习：

3. 小结

各种码的作用（拓展）

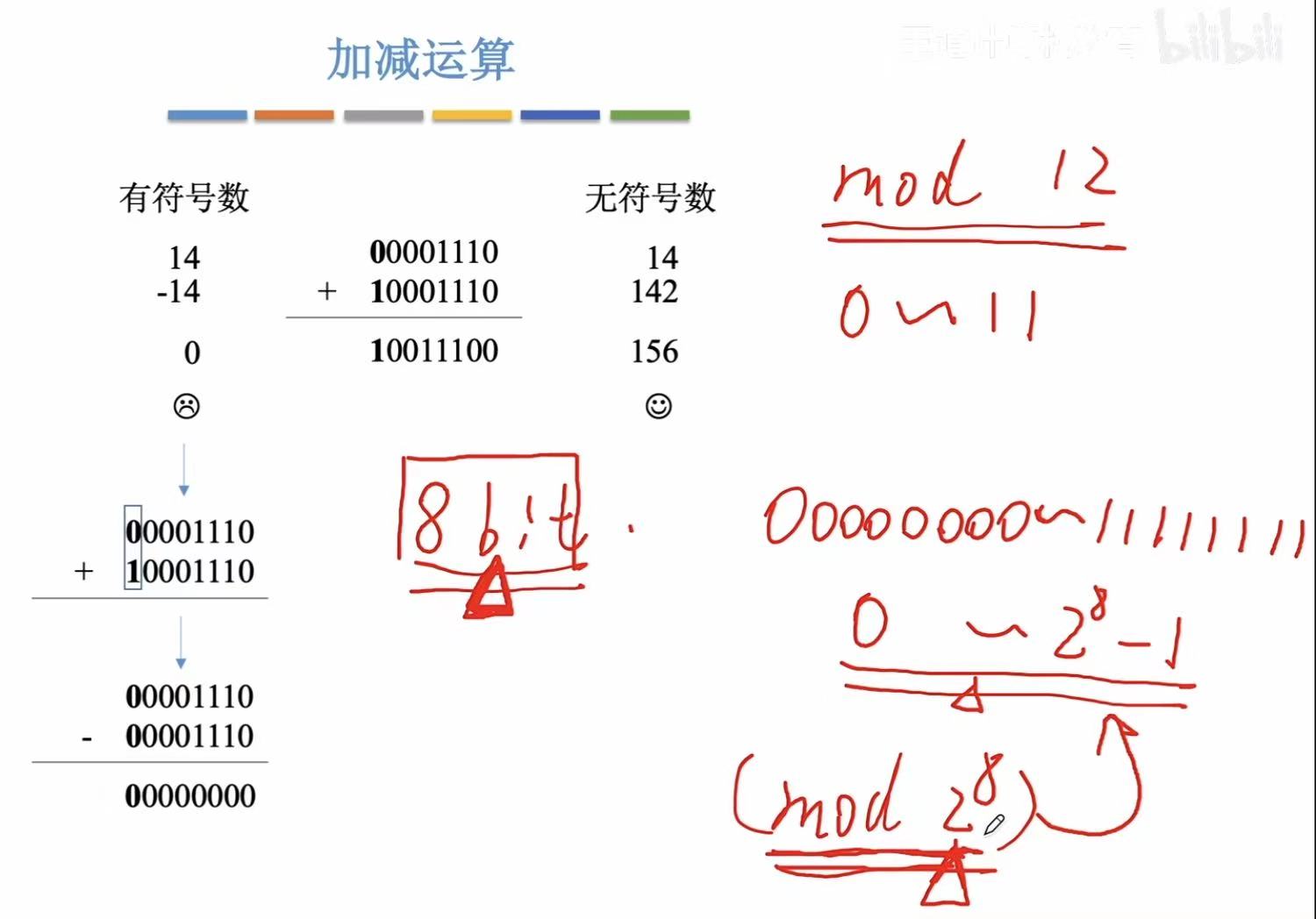
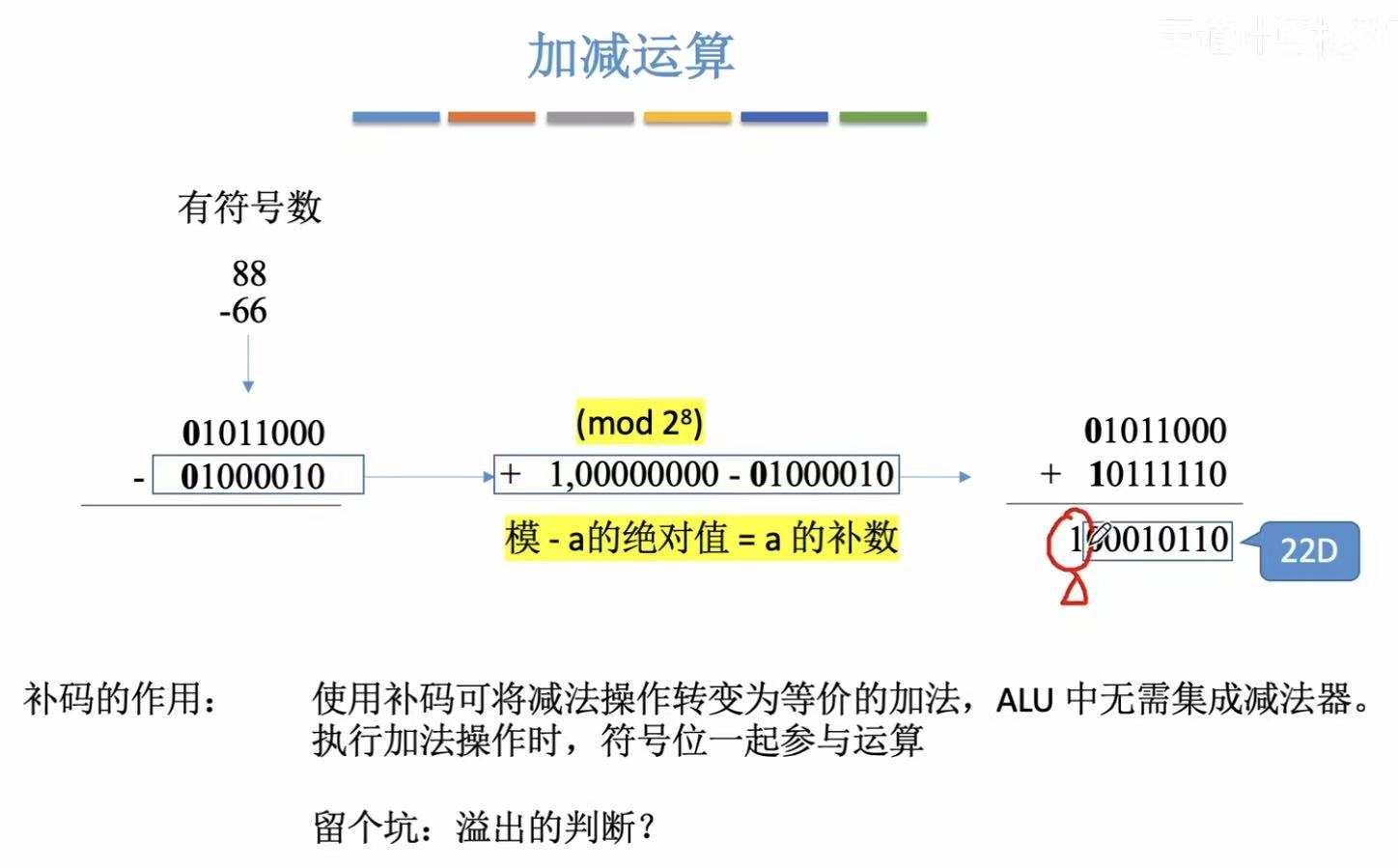
用原码算减法，因为有正负符号位的区分，所以无法得出正确结果。
所以人们就想到了能不能用加法来代替减法，同时：在做物理组件的时候用一个组件直接实现两个功能可以解决成本。

就像时钟一样，人们引入了模的概念。
比如你想将指向10的时针调到5，可以顺时针调7下：（10+7）/12=5，也可以逆时针调5下：（10-5）/12=5。

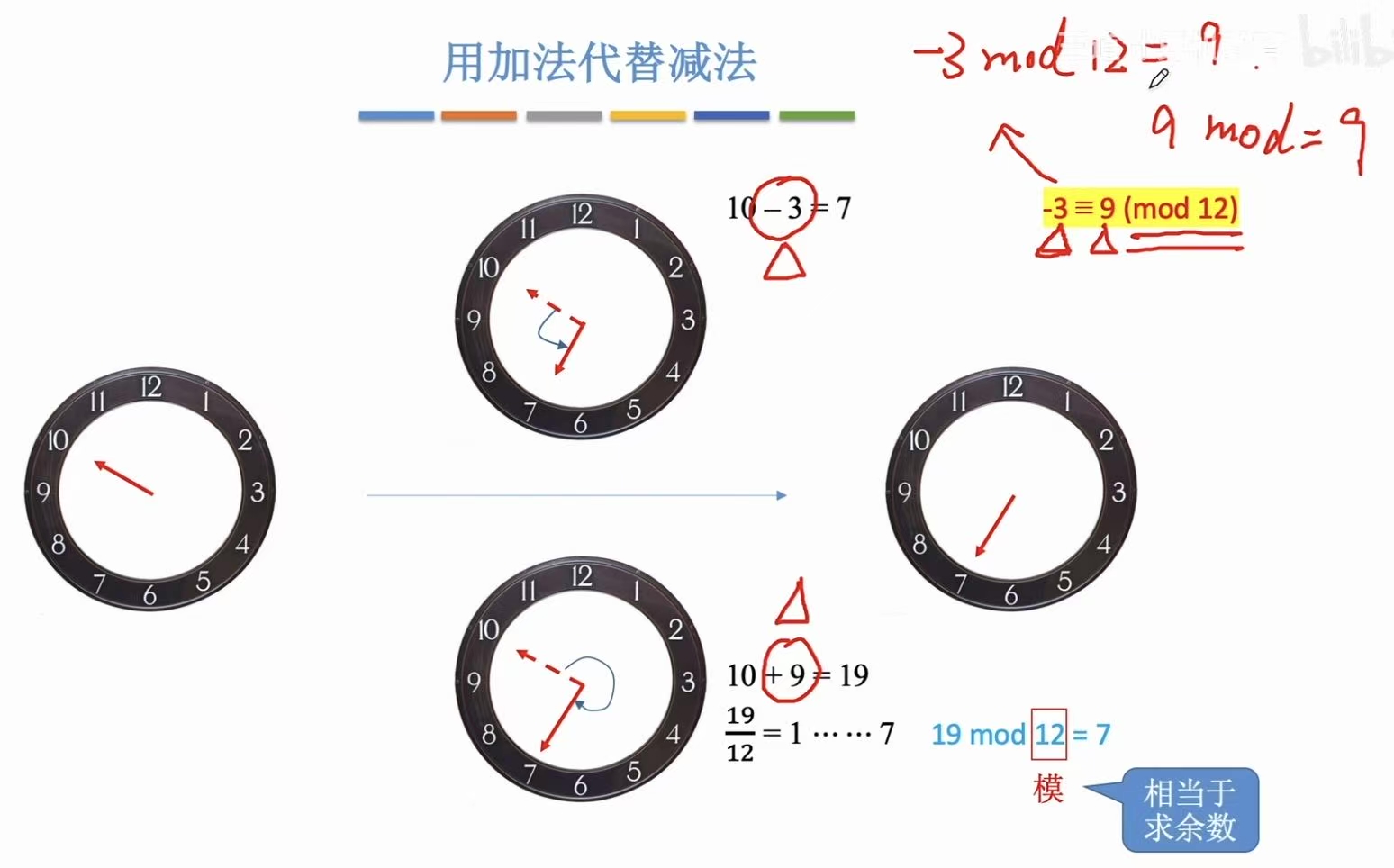
模12就是把数分成了12类，就像时针只能指到1~12一样。

模2^8就是把数分成从0~255，二进制来看就是0000 0000 ~ 1111 1111，也就是全部八位的二进制数。

a的补数就是a的补码，其实是由模-a的绝对值才出现的。
（注意：这里出现了补码，所以原码的加减计算可以用补码解决）

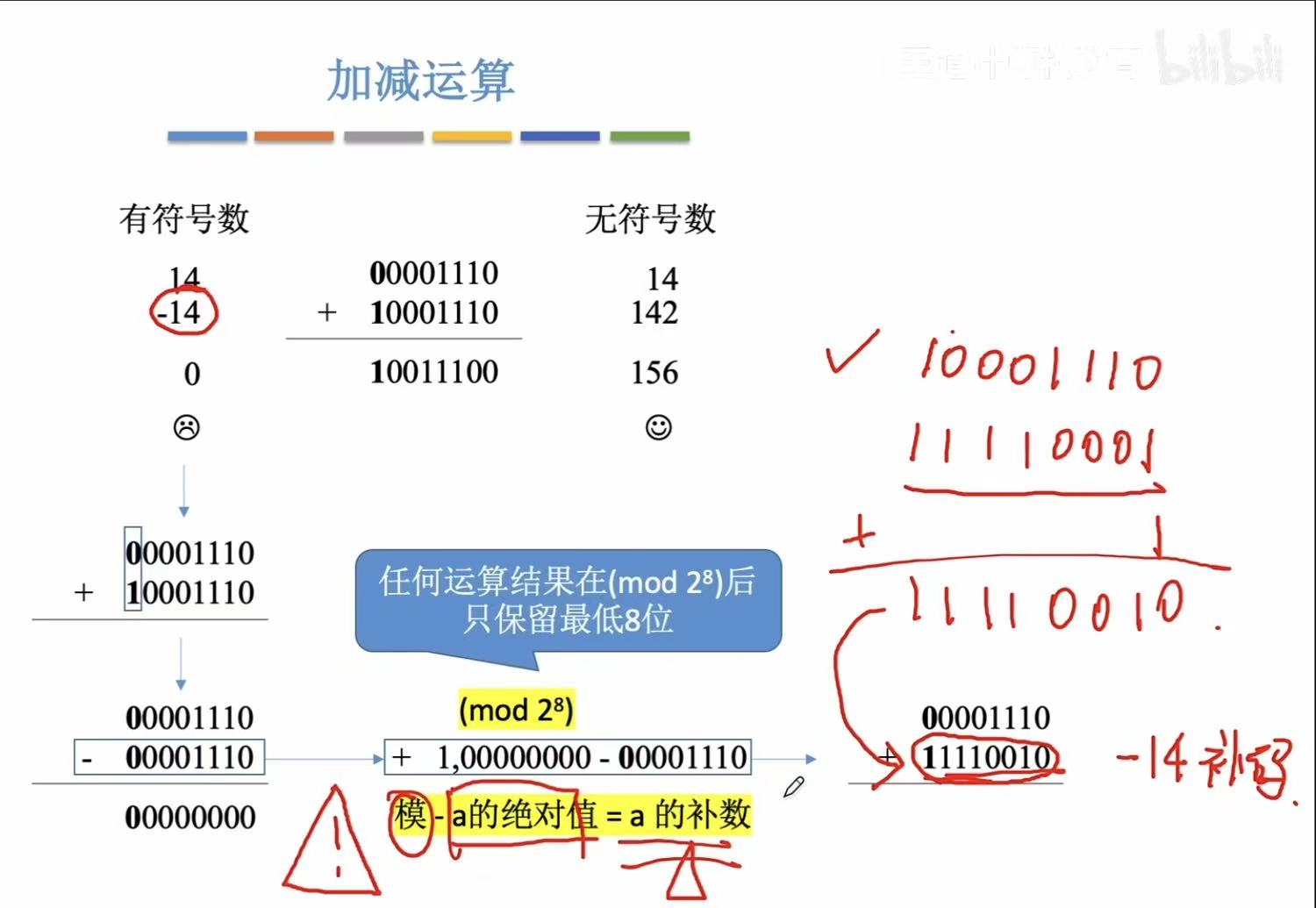
所以原码的加减运算，就可以转换为补码的加法运算。
这就是补码存在的意义。

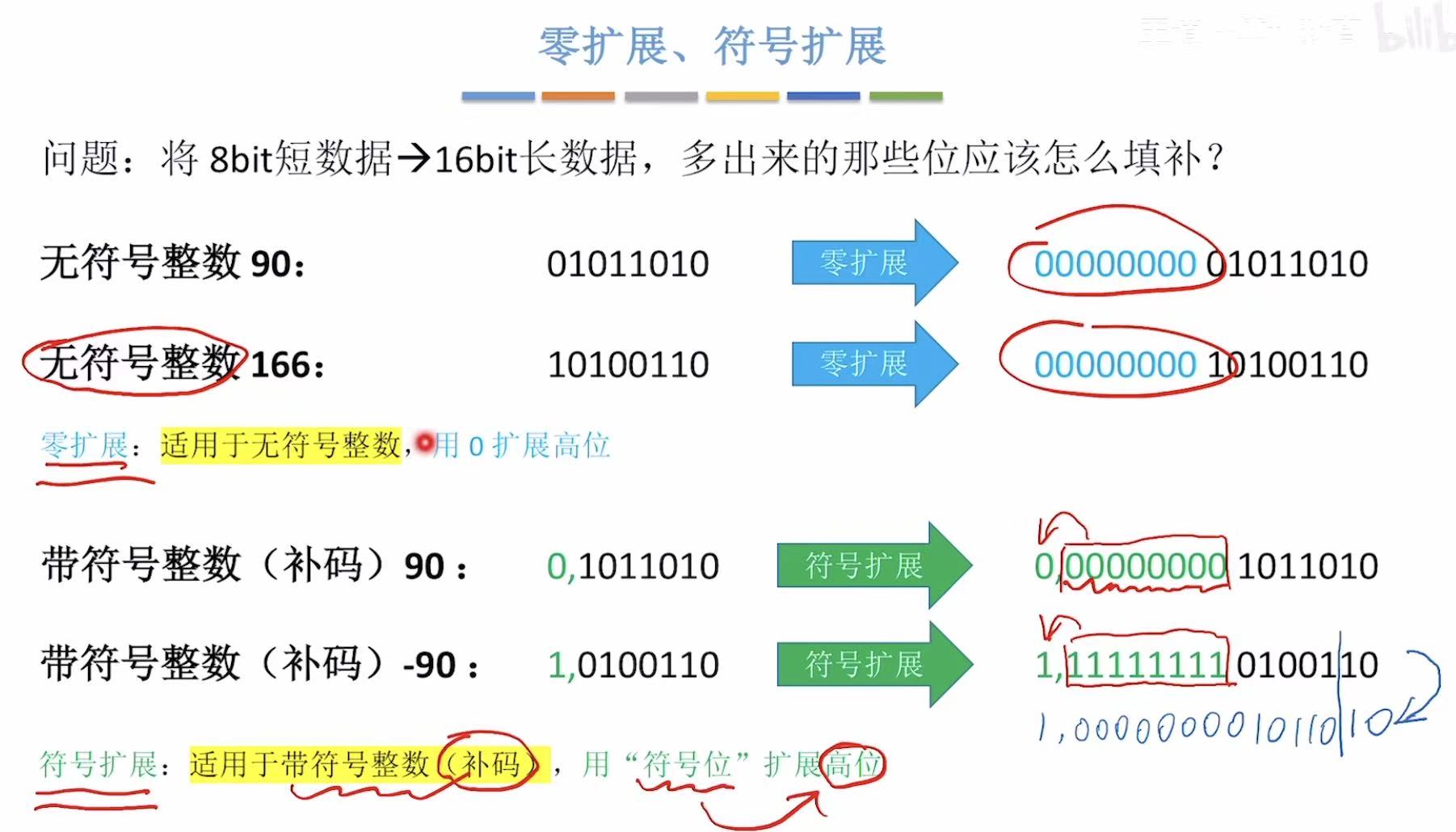
零拓展&符号拓展

强制类型转换

short：没说unsigned就是有符号数。
usigned short：无符号的short类型的数。

无符号数与有符号数：转换成什么数，就用那个类型的数的解释方式。
长整数变短整数：高位截断，保留低位。
短整数变长整数：符号拓展。