表面参数化

离散调和映射

凸组合映射

这个定理的证明能够被扩展为：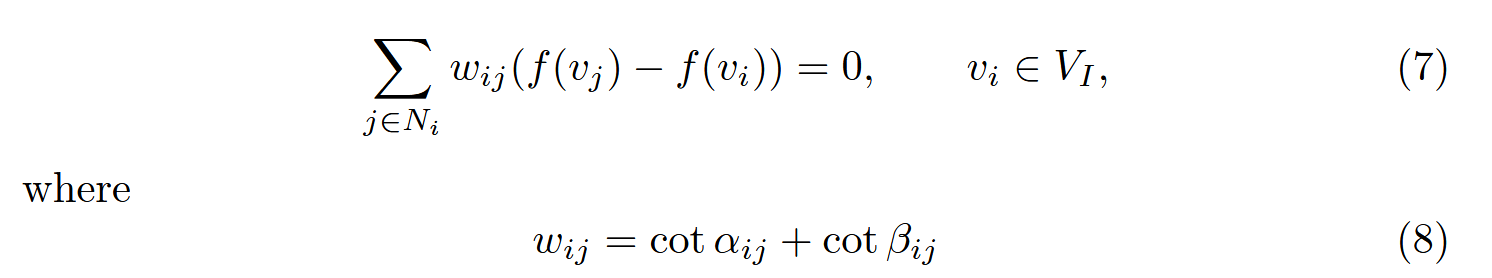

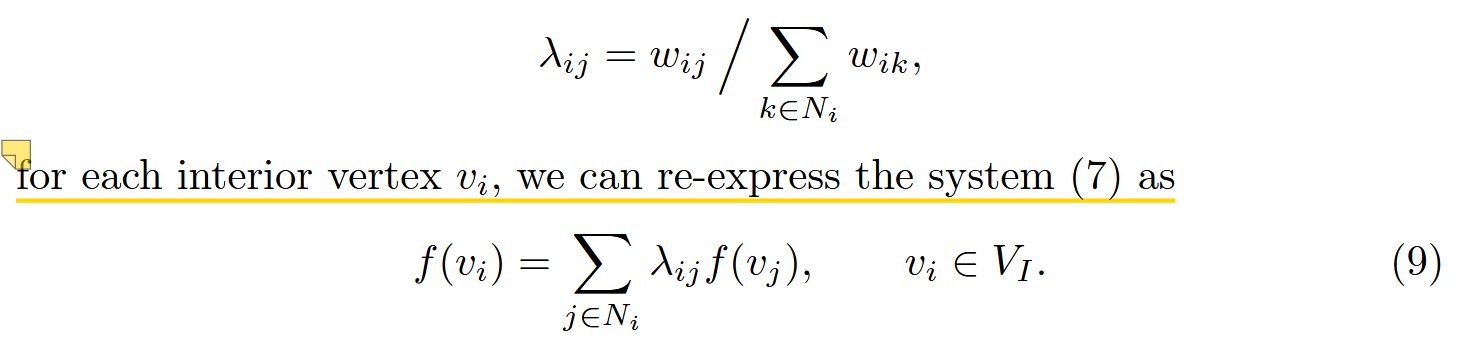
(7)(8)是确保参数化后局部畸变小，整体协调性好的条件。而通过变形可以将(7)变为(9)的形式，自然就有：

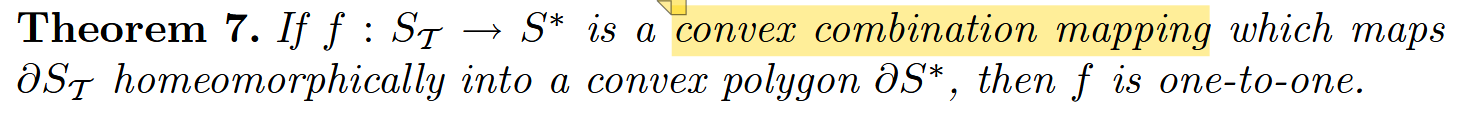
又有，对(8)式进行变形，

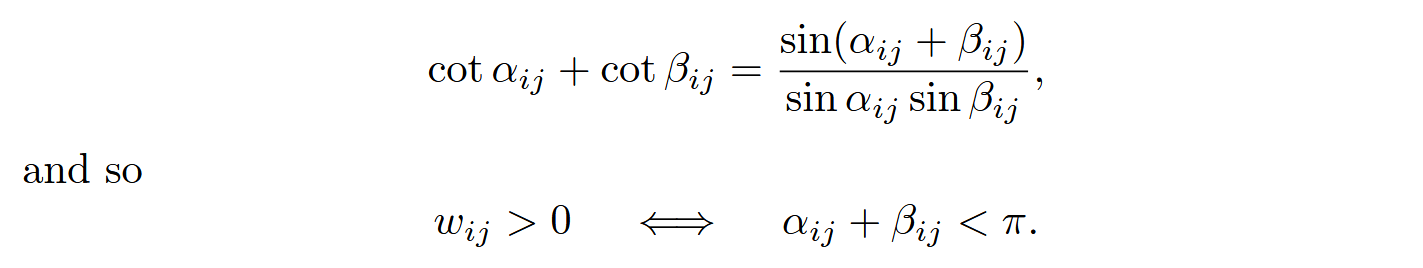
这里说明了如果一个离散调和映射要是一一对应的话（三角网格），除了凸边界要对应之外还有每个三角形都是锐角三角形

Mean value coordinates（均值坐标）

我们追求映射尽量有等距的性质，因此我们给出一种再现性质：

再现性质

当一个映射满足这个性质时（因为这个再现性质其实是一个特例），则这个映射具有两个的保等距性质
调和映射有这个性质，这就是为什么调和映射有接近保型映射的效果。

均值坐标

一种同时简化共型映射和离散调和映射的方法
在（平面）定义域的每一点上，调和函数的值等于以该点为中心的任何圆周上其值的平均值。
公式：

通过一些代数变换可以将其等价于(7)式，并且将Wij变为：

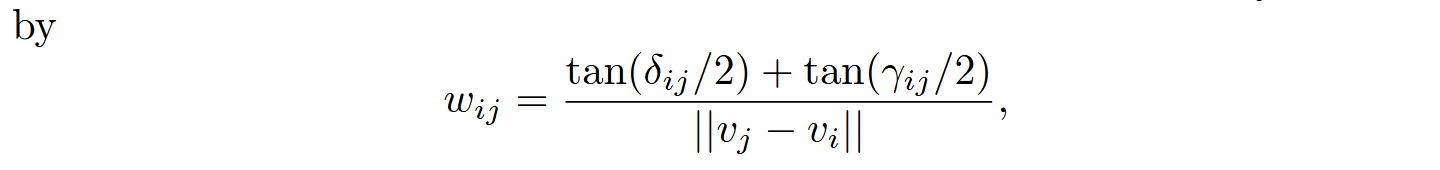
这样就将调和映射进行了离散化。

能量最小化

之前我们谈论的参数化方法都可以看作一种能量最小化，但是均值坐标这种方法目前还不知道是什么能量最小化。

边界映射

选择形状

我们通常选择一个凸形状作为参数域。
当原曲面边界不是凸的时候，映射在边界处会发生较大的变形。
一种方法是增加三角形改善边界。

选择边界分布

由黎曼映射定理有，一个光滑且有光滑边界的曲面，能共形的映射到参数域。
而这样的一个映射能诱导处一个良好的边界映射。
从中得到启发，一个良好的边界映射应该存在一种调和映射，是得这个映射对于整个平面式共形的。
因此，很多分段线性映射会对整个边界或是单个边界进行简单映射。（追求一个好的边界）
而如何将边界点分不到映射的特定区域内最大化共形形任然是一个问题。

离散共形映射

前面的参数化方法都是将曲面边界映射为固定的边界，但由上一章边界映射可知，优化边界的映射可以得到更加共形的效果。
我们在分段线性映射中有诸多方法不要求映射到特定形状中，但能尽量保持共形。

“most isometric parameterizations” (MIPS)

非退化的二维线性方程：就是有两个二元方程的方程组，其中参数可以构成一个雅可比矩阵。非退化指的是这个二维到二维的变化不能把多个点映射到一个点，即雅可比矩阵不为0.

Frobenius是一种范数，用来衡量矩阵整体的大小；norm这里指的是范数下，是衡量矩阵在数值计算中“稳定性”的一个重要量。这里用这种方法来衡量雅可比矩阵的拉伸程度

Frobenius范数的计算结果如上图所示：
有基本不等式可得：$\sigma 1=\sigma 2$时，取得最小值，最稳定。而这时正好是共性映射。

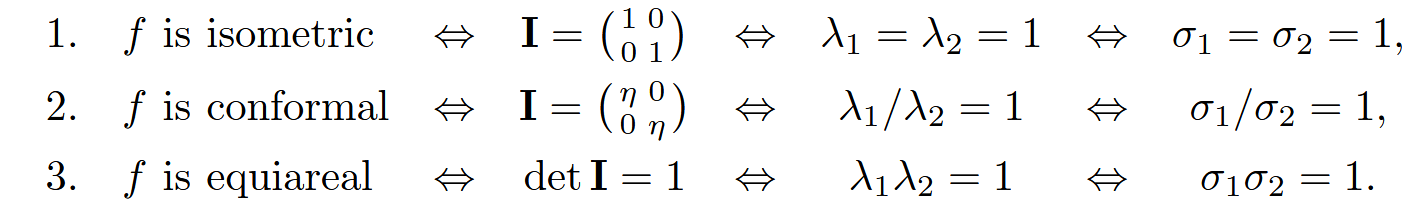
则在分段线性映射中有：

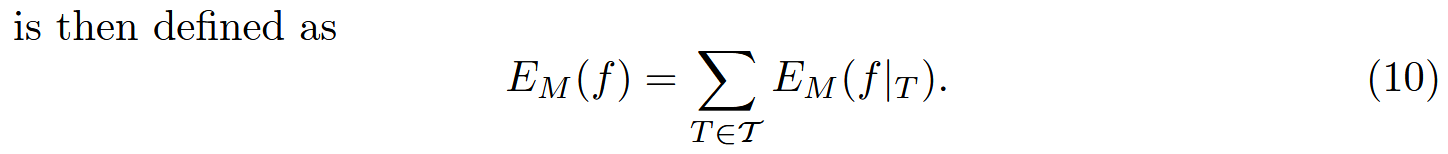
当映射是共形时，其能量最小且刚好为三角形数量的两倍。
并且共形映射如果是保形的话必须是可展的平面，而且映射会是等距的。
这种参数化叫：“most isometric parameterizations” (MIPS).

如何做到最小化MIPS能量

基于角度的扁平化

思想概述：可以理解为将三角网格展平为平面时，每个顶点周围角度的变化尽量均摊在每个角上。最小化角度的平均变化幅度与每个角实际变化之差的平方。这样就处理为了一个最小化问题。

线性方法

这一方法的来源是最小化对于柯西黎曼条件的违反程度。
柯西黎曼条件：

可以从上面的方程看到当映射满足柯西黎曼条件时能量最小化为9.

离散等积映射

通过最小化这个式子来确保等积：

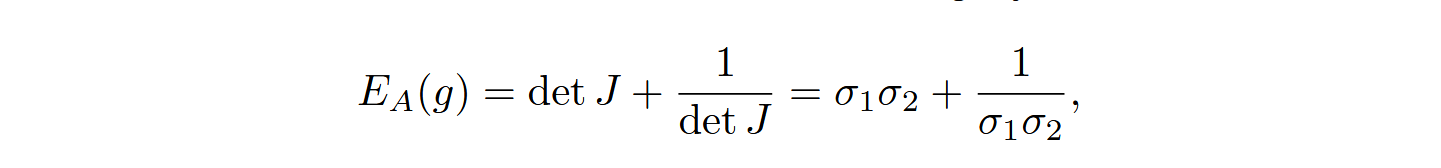
可以看到，当映射为等积映射时这个能量最小。

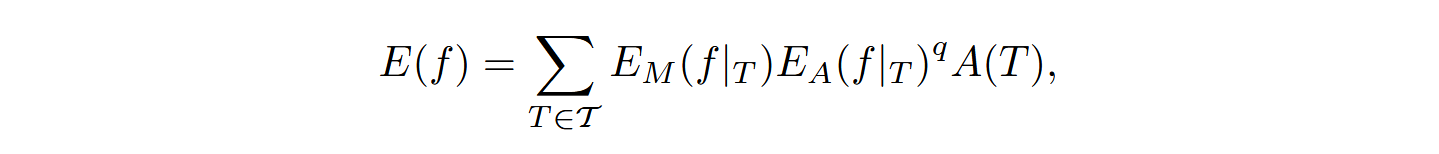
可以看到最小化这个能量时，能同时保持共形和等积两个性质。
也有一种衡量拉升程度的最小化方法：