CF Round 1027 Div.3 vp补题

原题链接
补题参考

C 1000 dp 贪心

注意到$a_i\le a_{i+1}$，可以对每种数进行dp，$dp[num]=max(dp[num-1\sim num],dp[num-2]+1,dp[前一个划分的末尾]+1)$

void solve()
{int n,mx=0;cin>>n;vector<int>a(n+2,0);forr(i,1,n){cin>>a[i];mx=max(mx,a[i]);}vector<int>dp(mx+1,0);map<int,int>rec;dp[a[1]]=1;rec[a[1]]=1;forr(i,2,n){dp[a[i]]=max(dp[a[i]],dp[a[i]-1]);if(a[i-1]+1<a[i])dp[a[i]]=max(dp[a[i-1]]+1,dp[a[i]]);//能划分else {//没有划分 连着的if(rec[a[i]-2])dp[a[i]]=max(dp[a[i]-2]+1,dp[a[i]]);//想再搞出一个划分 必须去掉num-1 从num-2和num之间划分}rec[a[i]]=1;}cout<<dp[a[n]]<<endl;
}

D 1400 暴力枚举 思维

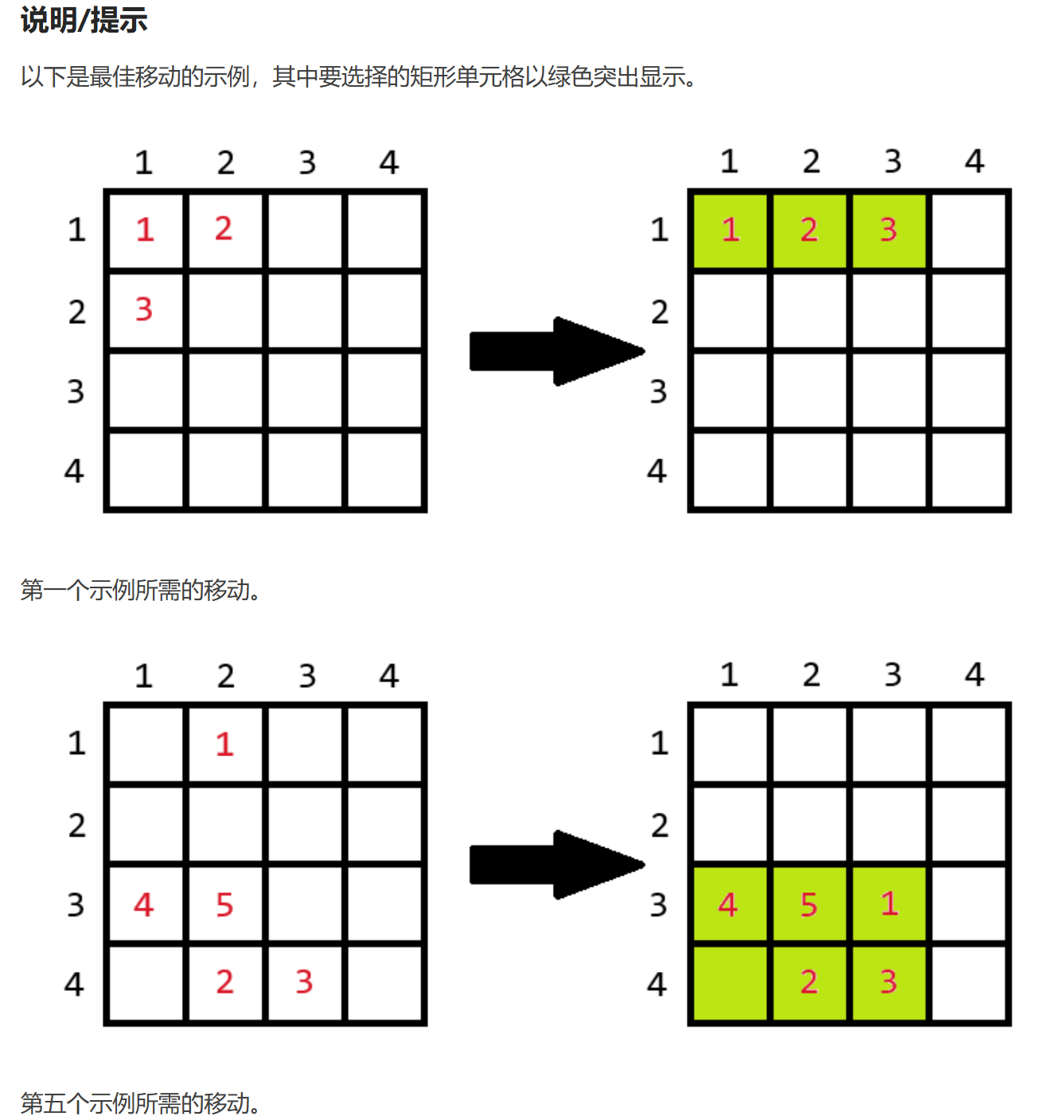
使用multiset排序，找矩形的最大范围

void extract(multiset<int>&s,int aim){auto it=s.find(aim);if(it!=s.end())s.erase(it);//或者可以直接s.erase(s.find(aim));
}
void solve()
{int n;cin>>n;vector<pii>p(n+1);multiset<int>dx,dy;forr(i,1,n){cin>>p[i].x>>p[i].y;dx.insert(p[i].x);dy.insert(p[i].y);}if(n==1)return cout<<1<<endl,void();int ans=(*dx.rbegin()-*dx.begin()+1)*(*dy.rbegin()-*dy.begin()+1);forr(i,1,n){//暴力枚举每一个去掉的情况// dx.erase(p[i].x),dy.erase(p[i].y);错了 这样会把multiset中所有该数都去掉extract(dx,p[i].x),extract(dy,p[i].y);// extract方法用于从multiset中移除指定节点并返回一个处理该节点的对象，这使得可以在不破坏原始容器的情况下操作数据//C++17标准中引入，不知道为什么我的编译器用不了int a=*dx.rbegin()-*dx.begin()+1,b=*dy.rbegin()-*dy.begin()+1;int sm=a*b;if(sm<n){//不够放移过来的那个ans=min({ans,sm+a,sm+b});//多加一行或一列}else ans=min(ans,sm);dx.insert(p[i].x),dy.insert(p[i].y);}cout<<ans<<endl;
}

E 1400 贪心 dfs 树

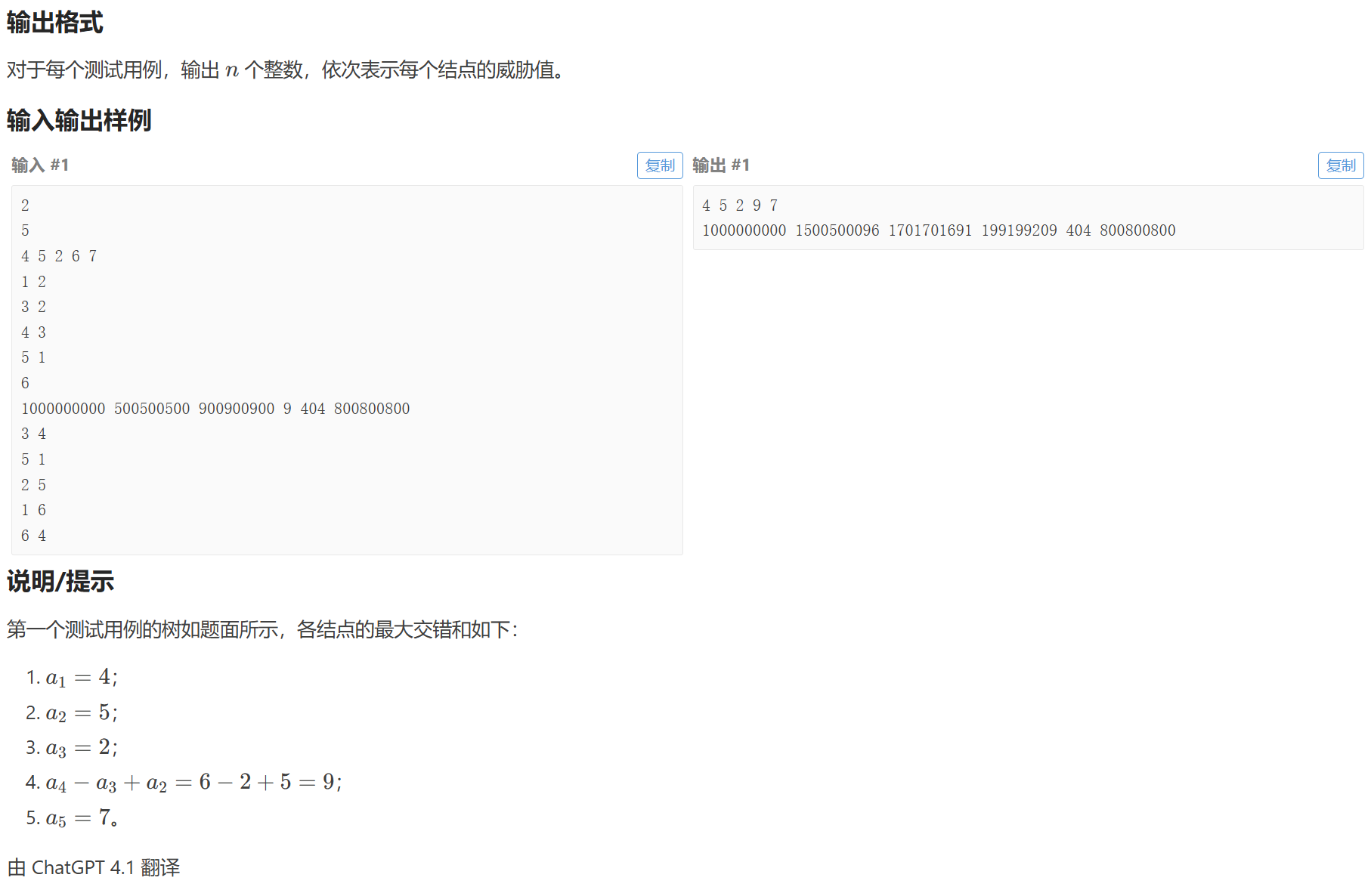
思路：从上往下递推，本节点要取最大值，就需要$a[now]-父节点最小值$，然后每个节点的答案就是递推到本节点的最大值

const int N = 2e5+10, C = 1e6 + 10, mod =998244353, inf = 1e18 ;
vector<int>g[N];
int a[N],mx[N],mn[N];
int n;
void dfs(int now,int fa){
//更新本节点最大最小值mx[now]+=a[now];mn[now]+=a[now];for(auto x:g[now]){if(x==fa)continue;//上面的更新下面的mx[x]=max({0ll,-mx[now],-mn[now]});//注意可以不加上面的 拿0ll去比mn[x]=min(-mx[now],-mn[now]);dfs(x,now);}
}
void solve()
{cin>>n;forr(i,1,n)cin>>a[i];forr(i,1,n)g[i].clear();forr(i,1,n-1){int u,v;cin>>u>>v;g[u].push_back(v);g[v].push_back(u);}mx[1]=mn[1]=0;dfs(1,0);forr(i,1,n)cout<<max(mx[i],mn[i])<<' ';cout<<endl;
}

F 2000 dp 思维 数学 贪心

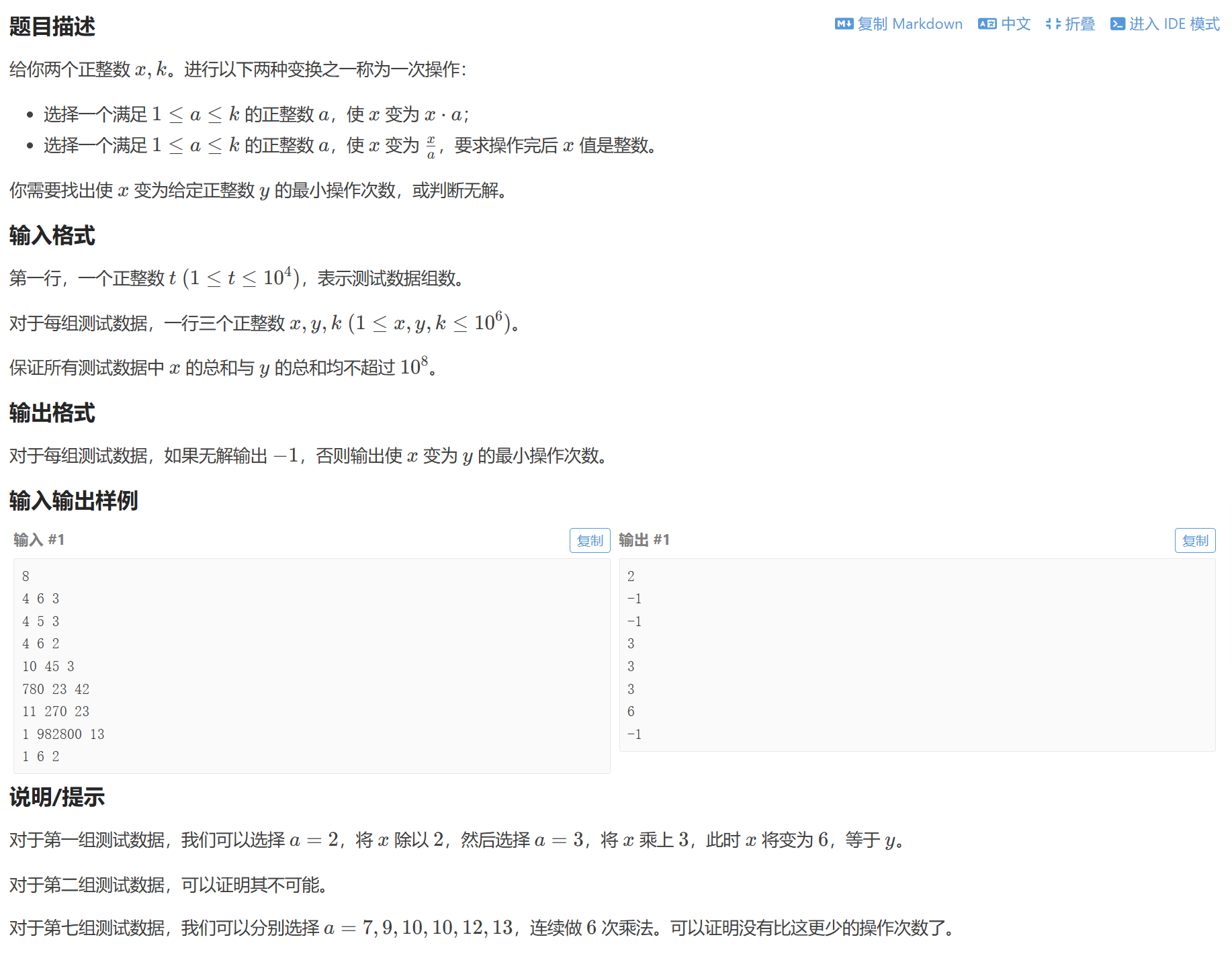
直观来想就要在x中除去y中没有的因数，添加y中多的因数
最小次数是$x\to gcd(x,y)\to y$即$x/gcd\to 1\to y/gcd$

const int N = 1e6+10, C = 1e6 + 10, mod =998244353, inf = 1e18 ;
vector<int>g[N];
int x,y,k;
void init(){//找每个数的所有因数复杂度O(NlogN)g[1].push_back(1);forr(i,2,N-5){g[i].push_back(1);for(int j=i;j<=N-5;j+=i){g[j].push_back(i);}}forr(i,2,N-5)sort(g[i].begin(),g[i].end());}
int op(int x){// dp求1->x的最小次数int n=g[x].size();vector<int>dp(n,inf);dp[0]=0;forr(i,0,n-1){if(dp[i]==inf)continue;forr(j,i+1,n-1){if(g[x][j]%g[x][i]==0&&g[x][j]/g[x][i]<=k)dp[j]=min(dp[j],dp[i]+1);//更新最小次数else if(g[x][j]/g[x][i]>k)break;}}if(dp[n-1]==inf)return -1;else return dp[n-1];
}
void solve()
{cin>>x>>y>>k;int g=__gcd(x,y);x/=g,y/=g;//除去公共部分 最小次数就是x->g->y// cout<<x<<' '<<y<<endl;if(x==y)return cout<<0<<endl,void();int ansx=op(x),ansy=op(y);if(ansx==-1||ansy==-1)cout<<-1<<endl;else cout<<ansx+ansy<<endl;
}
signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int _ = 1;init();cin >> _;while (_--){solve();}return 0;
}