4.寻找两个正序数组的中位数

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。算法的时间复杂度应该为 O(log (m+n)) 。（暗示我们用二分法）

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

一. 暴力解法

长度之和为奇数时，返回1个中位数；长度之和为偶数时，返回合并排序后中间两数的平均数。

如果不考虑复杂度的限制，可以想到先合并两个数组，再排序找到中位数。这个方法的弊端是浪费了“数组正序”的条件。时间复杂度取决于排序算法的时间复杂度，利用快速排序算法，它的时间复杂度是  。

合并两个有序数组，可以利用双指针比较元素大小，按序插入新的数组中。遍历完两个有序数组，可以得到一个更大的有序数组。归并排序的合并步骤，它的时间复杂度为  。

二. 二分查找

2.1 基于中位数的作用

在统计中，中位数被用来：将一个集合划分为两个长度相等的子集，其中一个子集中的元素总是大于另一个子集中的元素。中位数只跟分割线两边的元素有关，这道题可以转化成寻找两个正序数组中的分割线。

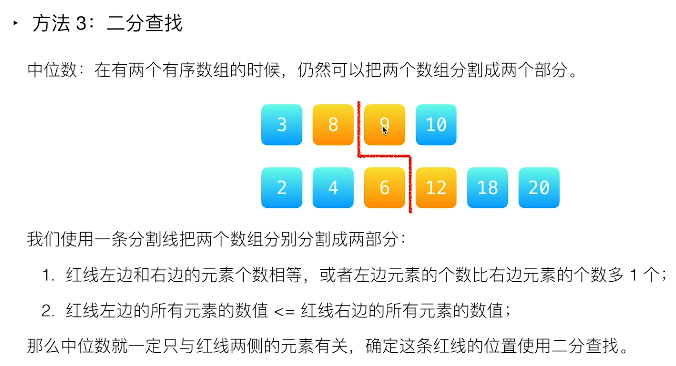
我们不必分别去确定分割线在两个数组中的位置，分割线两侧元素的数量是可以计算出来的。

需要额外确认：

• 第一个数组在分割线左边的最大值 小于 第二个数组在分割线右边的最小值。
• 第二个数组在分割线左边的最大值 小于 第一个数组在分割线右边的最小值。

2.2 基于中位数的计算

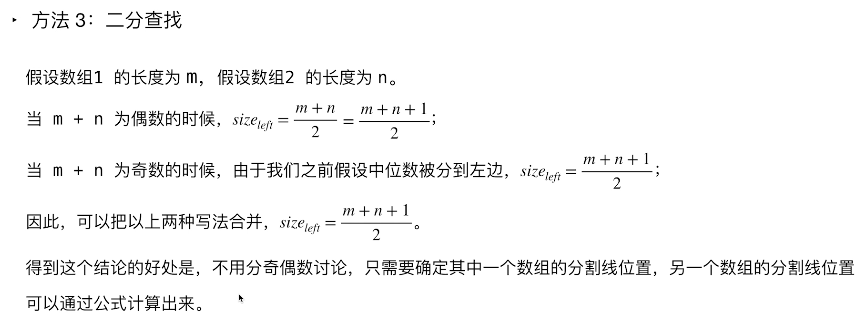
根据中位数的定义，当 m+n 是奇数时，中位数是两个有序数组中的第 (m+n)/2 个元素，当 m+n 是偶数时，中位数是两个有序数组中的第 (m+n)/2 个元素和第 (m+n)/2+1 个元素的平均值。

因此，这道题可以转化成寻找两个有序数组中的第 k 小的数，其中 k 为 (m+n)/2 或 (m+n)/2+1。

寻找两个有序数组中的第 k 小的数，可以先比较 A[k/2−1] 和 B[k/2−1] 之后，可以排除 k/2 个不可能是第 k 小的数，查找范围缩小了一半。同时，我们将在排