大规模组合优化问题的统一神经分治框架(NIPS‘24)

Abstract

单阶段神经组合优化求解器无需依赖专家知识，便已在各类小规模组合优化（CO）问题上取得了接近最优的结果。然而，将这类求解器应用于大规模组合优化问题时，其性能会出现显著下降。近年来，受分治策略启发的两阶段神经方法在处理大规模组合优化问题时展现出一定效率，但这些方法的性能在分解或求解过程中高度依赖问题特定启发式方法，这限制了它们在通用组合优化问题中的适用性。此外，这些方法采用分开训练方案，忽略了分解与求解策略之间的相互依赖关系，往往会导致生成次优解。

为解决上述缺陷，本文提出了一种用于求解通用大规模组合优化问题的统一神经分治框架（UDC）。该框架提供了一种“分解-求解-重组”（Divide-Conquer-Reunion，DCR）训练方法，可消除次优分解策略带来的负面影响。UDC采用高效图神经网络（GNN）进行全局实例分解，并使用定长子路径求解器处理分解后的子问题，最终展现出广泛的适用性，在10类具有代表性的大规模组合优化问题中均实现了卓越性能。

代码获取地址：https://github.com/CIAM-Group/NCO_code/tree/main/single_objective/UDC-Large-scale-CO-master

Introduction

组合优化（CO）[1]具有众多实际应用，包括路径规划[2]、电路设计[3]、生物学[4]等领域。过去几年间，研究人员开发了神经组合优化（NCO）方法，以高效求解旅行商问题（TSP）、带容量约束的车辆路径问题（CVRP）等典型组合优化问题。其中，基于强化学习（RL）的构造性神经组合优化方法[5,6]无需依赖专家知识，便能为小规模实例（例如节点数不超过200的TSP实例）生成接近最优的解[7]。这类求解器通常采用单阶段解生成流程，以端到端的方式逐节点构建组合优化问题的解。然而，由于无法直接在更大规模实例上进行训练[8,9,10]，这些方法在推广用于求解大规模组合优化问题时，性能表现受限。

为满足大规模组合优化应用的需求，研究人员已越来越多地致力于将神经组合优化方法扩展至更大规模实例（如1000节点实例）[11]。目前针对大规模问题的神经组合优化方法主要包括改进型单阶段求解器[6]和神经分治方法[12,13]。BQ-NCO[14]与LEHD[8]构建了子路径构造流程[15]，并采用带有重型解码器的模型来学习该流程。但训练此类重量级模型需要依赖监督学习（SL），这限制了它们在无法获取高质量标签解的问题中的适用性。ELG[6]、ICAM[16]与DAR[17]则整合辅助信息，以引导基于强化学习的单阶段构造性求解器[5]进行学习。然而，辅助信息需针对具体问题进行定制设计，且自注意力机制带来的O(N²)复杂度，也给大规模（N节点）问题的求解带来了挑战。

作为大规模神经组合优化的另一类方法，神经分治方法受到了越来越多的关注。这类方法受传统启发式算法中常见分治思想[18,19]的启发，执行两阶段求解流程：包括对整体实例进行划分的分解阶段，以及对子问题进行求解的求解阶段。通过在一个或两个阶段中采用神经网络，TAM[12]、H-TSP[20]与GLOP[13]已在大规模TSP和CVRP问题中展现出更优的效率。

尽管认可其应用前景，这些神经分治方法在适用性和求解质量方面仍存在不足。部分神经分治方法在分解阶段（如GLOP[13]、SO[21]）或求解阶段（如L2D[22]、RBG[23]）依赖问题特定的启发式方法，这限制了它们在各类组合优化问题中的泛化能力。此外，现有所有神经分治方法均采用分开训练方案：先预训练求解策略，再基于预训练好的求解策略训练分解策略[13,12,20]。然而，这种分开训练方案忽略了分解策略与求解策略之间的相互依赖关系，可能导致难以调和的对抗性问题。一旦预训练的求解策略对某些子问题而言并非最优，这种训练方案可能会引导分解策略去适配预训练的次优求解策略，进而收敛到局部最优。

如表1所示，本文发现：若要生成高质量的分治基解，必须考虑次优分解结果带来的负面影响。为此，本文提出一种基于强化学习的新型训练方法，称为“分解-求解-重组”（Divide-Conquer-Reunion，DCR）。通过在统一训练方案中引入DCR，本文提出了适用于各类大规模组合优化问题的统一神经分治框架（UDC）。UDC采用快速轻量的图神经网络（GNN）将大规模组合优化实例分解为多个定长子问题，并利用构造性求解器对这些子问题进行求解。

本文在10类不同的组合优化问题上开展了大量实验。实验结果表明，在不依赖任何启发式设计的情况下，UDC在求解效率和适用性两方面均显著优于现有大规模神经组合优化求解器。

本文的贡献如下：1）提出新型方法DCR，通过减轻次优分解策略的负面影响来改进训练；2）将DCR应用于训练过程，所提UDC框架实现了统一训练方案，并获得显著更优的性能；3）UDC展现出广泛的适用性，可应用于具有相似设定的通用组合优化问题。

2 预备知识：神经分治

2.1 分治

具有$N$个决策变量的组合优化（CO）问题被定义为最小化解$\boxed{x}=(x_1,x_2,\dots ,x_N)$的目标函数$f$，形式如下：
$$\underset{\boxed{x}\in \Omega }{\mathrm{最小化}}f(\boxed{x},\mathcal{G})\text{\hspace{1em}(1)}$$
其中$\mathcal{G}$表示组合优化实例，$\Omega$是由所有可行解组成的集合。

在传统（元）启发式算法[25]中，利用分治思想求解组合优化问题具有前景，尤其是基于大邻域搜索的算法[26,27]。这些方法通过迭代的子问题选择（即分解阶段）和子问题修复（即求解阶段），从初始解开始逐步提升性能。近期的神经分治方法执行类似的求解过程，并采用高效的深度学习技术对两个阶段的策略进行建模[13]。分解策略${\pi }_d(\mathcal{G})$将实例$\mathcal{G}$分解为$K$个相互独立的子问题{G1,G2,…,GK}\{\mathcal{G}_1, \mathcal{G}_2, \ldots, \mathcal{G}_K\}{G1​,G2​,…,GK​}，求解策略${\pi }_c$通过$s_k\sim {\pi }_c({\mathcal{G}}_k)$为k∈{1,…,K}k \in \{1, \ldots, K\}k∈{1,…,K}生成子解$s_k$，以最小化对应子问题的目标函数$f^{\prime }(s_k,{\mathcal{G}}_k)$。最后，$\mathcal{G}$的完整解$\boxed{x}$通过$\boxed{x}=\text{Concat}(s_1,\dots ,s_K)$拼接得到。

2.2 构造性神经求解器

（单阶段）构造性神经组合优化（NCO）求解器在高效求解通用小规模组合优化（CO）问题方面颇具前景。这些构造性求解器通常采用基于注意力的编码器-解码器网络结构，其中多层编码器将组合优化实例处理为隐藏空间中的嵌入表示，轻量级解码器在构建可行解的同时处理动态约束[5]。通过将求解过程建模为马尔可夫决策过程（MDPs）[28]，构造性求解器可利用深度强化学习（DRL）技术进行训练，无需依赖专家经验。

在解生成过程中，参数为$\theta$的构造性求解器对长度为$\tau$的解$\boxed{x}=(x_1,\dots ,x_{\tau })$的策略$\pi$按如下方式处理：
$$\pi (\boxed{x}|\mathcal{G},\Omega ,\theta )=\prod _{t=1}^{\tau }{p}_{\theta }(x_t|{\boxed{x}}_{1:t-1},\mathcal{G},\Omega ),\text{\hspace{1em}(2)}$$
其中${\boxed{x}}_{1:t-1}$表示选择$x_t$之前的部分解。

基于深度强化学习的构造性神经组合优化求解器在小规模组合优化问题中展现出卓越的解质量。因此，现有神经分治方法[13,21]通常也会为其求解策略${\pi }_c$采用预训练的构造性神经求解器（例如注意力模型[28]）。

2.3 基于热图的神经求解器

先进的构造性神经组合优化（NCO）求解器依赖自注意力层[29]进行节点表示，其与问题规模相关的二次时间和空间复杂度[30]阻碍了在大规模实例上的直接训练。因此，研究人员提出了基于热图的求解器[31,32]，通过轻量级图神经网络（GNN）[33]高效求解大规模组合优化（CO）问题。

在针对车辆路径问题（VRPs）的基于热图的求解器中，参数为$\varphi$的GNN首先在线性时间内[34]生成一个热图$\mathcal{H}\in {\mathbb{R}}^{N\times N}$，然后基于该热图并按照如下策略[35]构造可行解：
$$\pi (\boxed{x}|\mathcal{G},\Omega ,\theta )=p_{\theta }(\mathcal{H}|\mathcal{G},\Omega )p(x_1)\prod _{t=2}^{\tau }\frac{exp({\mathcal{H}}_{x_{t-1},x_t})}{{\sum }_{i=t}^{N}exp({\mathcal{H}}_{x_{t-1},x_i})},\text{\hspace{1em}(3)}$$

然而，非自回归生成的热图[36]排除了已构造部分解${\boxed{x}}_{1:t-1}$的顺序信息，这导致基于热图的求解器中的贪心解码策略质量较低，且这些求解器依赖搜索算法[37,38]来获取更高质量的解。

3 方法：统一分治

如图1所示，UDC遵循神经分治方法的通用框架[13]，通过两个不同阶段求解组合优化（CO）问题：分解阶段和求解阶段。

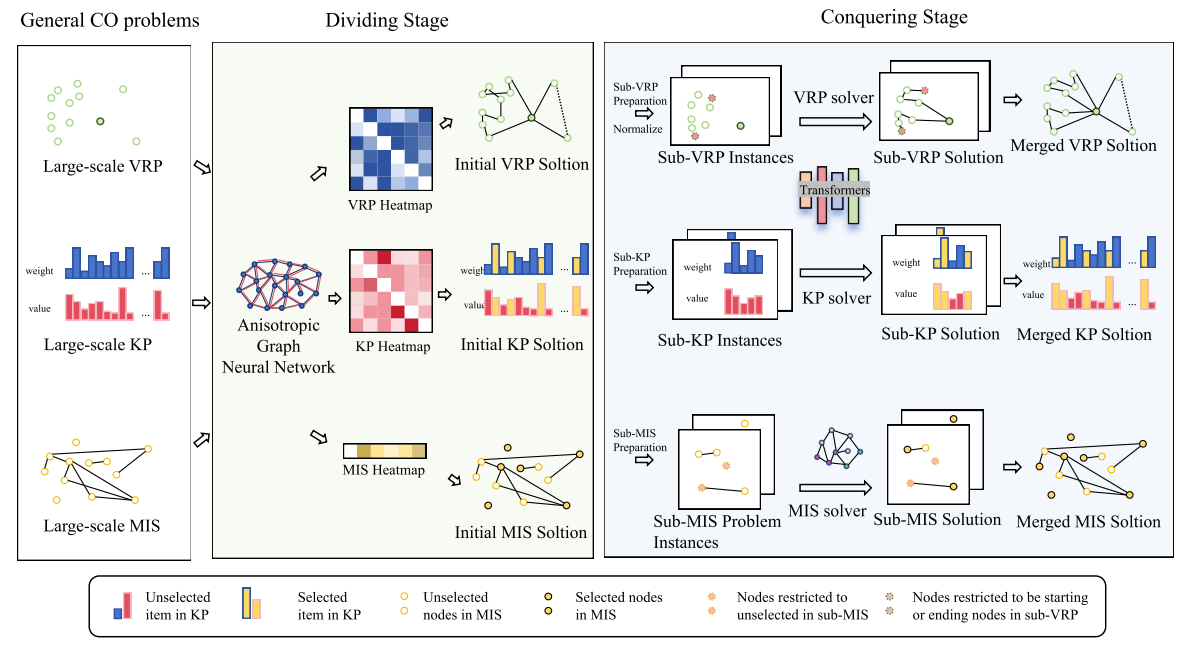
UDC的分解阶段期望生成与最优解整体形态相似的可行初始解，以便后续求解阶段可通过求解局部子问题获得更多高质量解。对于所有涉及的组合优化问题，UDC首先构建稀疏图来表示实例，然后采用基于 各向异性图神经网络（AGNN） 的热图求解器作为分解策略[39,40]以生成初始解。接下来的求解阶段首先基于初始解将原始组合优化实例分解为多个子问题，同时整合子问题的必要约束。然后，为了最小化子问题的分解目标函数，UDC采用构造性神经求解器作为求解策略来生成子解。由于不存在可处理所有类型组合优化问题的通用构造性神经求解器[41,42]，因此我们为每个子组合优化问题采用合适的求解器（例如，最大独立集（MIS）问题采用AGNN[39]，车辆路径问题（VRPs）采用POMO[5]或ICAM[16]）。

3.1 流程：分解阶段 & 求解阶段

分解阶段：基于热图的神经分解

基于热图的求解器与构造性求解器相比，时间和空间消耗更少，因此更适合在大规模实例上学习全局分解策略。分解阶段首先为原始组合优化实例$\mathcal{G}$构建稀疏图GD={V,E}\mathcal{G}_D = \{\mathbb{V}, \mathbb{E}\}GD​={V,E}（例如，在旅行商问题（TSP）中连接$K$近邻（KNN），或在最大独立集（MIS）问题中采用$\mathcal{G}$的原始边）。随后，我们利用带参数$\varphi$的 各向异性图神经网络（AGNN） 生成热图$\mathcal{H}$。对于含$N$个节点的车辆路径问题（VRP），热图$\mathcal{H}\in {\mathbb{R}}^{N\times N}$，长度为$\tau$的初始解${\boxed{x}}_0=(x_{0,1},\dots ,x_{0,\tau })$基于策略${\pi }_d$生成，形式如下：

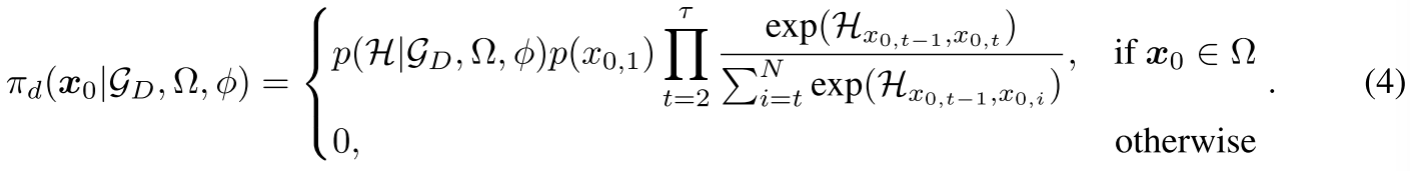
求解阶段：子问题准备

求解阶段首先生成待处理的子问题及其特定约束。对于VRP，子VRP中的节点和子VRP的约束基于初始解${\boxed{x}}_0$中的连续子序列构建。在生成含$n$个节点的子问题时，UDC根据${\boxed{x}}^0$将原始含$N$个节点的实例$\mathcal{G}$划分为$\lfloor \frac{N}{n}\rfloor$个子问题{G1,…,G⌊Nn⌋}\{\mathcal{G}_1, \ldots, \mathcal{G}_{\lfloor \frac{N}{n} \rfloor}\}{G1​,…,G⌊nN​⌋​}，暂时排除节点数少于$n$的子问题。子问题的约束{Ω1,…,Ω⌊Nn⌋}\{\Omega_1, \ldots, \Omega_{\lfloor \frac{N}{n} \rfloor}\}{Ω1​,…,Ω⌊nN​⌋​}不仅包含问题特定的约束（例如，子TSP中无自环），还包含额外约束以确保将子问题解整合到原始解后合并解的合法性（例如，保持子VRP中的首尾节点）。与先前工作[13,43]类似，我们也对亚问题的坐标和一些数值约束进行归一化，以增强待处理子问题实例的同质性。由于需要处理不同约束，不同组合优化问题的子问题准备过程有所不同，这在附录B中有详细说明。

求解阶段：构造性神经求解

在子问题准备完成后，求解策略被用于生成这些实例{G1,…,G⌊Nn⌋}\{\mathcal{G}_1, \ldots, \mathcal{G}_{\lfloor \frac{N}{n} \rfloor}\}{G1​,…,G⌊nN​⌋​}的解。对于大多数涉及的子组合优化问题，我们采用带参数$\theta$的构造性求解器。它们的子解${\boxed{s}}_k=(s_{k,1},\dots ,s_{k,n})$，k∈{1,…,⌊Nn⌋}k \in \{1, \ldots, \lfloor \frac{N}{n} \rfloor\}k∈{1,…,⌊nN​⌋}从求解策略${\pi }_c$中采样，形式如下：

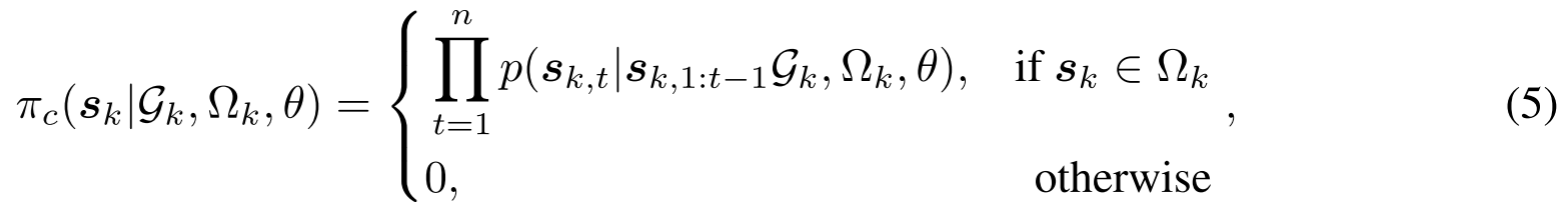
其中${\boxed{s}}_{k,1:t-1}$表示选择$s_{k,t}$之前的部分解。最后，作为求解阶段的最后一步，目标函数有所改进的子解将替换${\boxed{x}}_0$中的原始解片段，合并后的解变为${\boxed{x}}_1$。值得注意的是，求解阶段可在新的合并解上重复执行，以逐步提升解的质量，我们将经过$r$次求解阶段后的解记为${\boxed{x}}_r$。

3.2 训练方法：分解-求解-重组（DCR）

神经分治方法中的分解阶段和求解阶段均可建模为马尔可夫决策过程（MDPs）[12]（详见附录C.7）。求解策略的奖励源于子解的目标函数，而分解策略的奖励则基于最终合并解的目标函数计算。现有神经分治方法无法通过强化学习（RL）同时训练这两种策略[20]。因此，它们通常采用分开训练方案：先在特定数据集上预训练求解策略，再训练分解策略[13]。然而，这种分开训练过程不仅需要额外的问题特定数据集设计[13]，还会破坏分解与求解策略的协同优化（详见5.1节进一步讨论）。

本文提出，若要实现两种策略的统一训练，必须考虑次优子问题分解带来的负面影响。次优分解策略生成的子问题可能与最优解中的连续片段不匹配，如图2所示，即便获得高质量子解，这些子问题的连接区域也可能出现连接误差。神经分治方法的朴素求解流程忽略了解生成过程中这些不可避免的误差，从而利用有偏的奖励来评估分解策略。为解决这一缺陷，我们提出分解-求解-重组（DCR）流程，以尽可能消除该影响。DCR设计了一个额外的重组步骤：将原始两个相邻子问题的连接视为新子问题，并在${\boxed{x}}_1$上通过新的子问题分解执行另一轮求解阶段。重组步骤可表述为：将原始起始点$x_{1,0}$沿解${\boxed{x}}_{1,0}$滚动$l$次（即到$x_{1,l}$），再重新执行求解。为确保对相邻两个子问题的关注均衡，在所有启用DCR的UDC模型训练中，我们设置$l=\frac{n}{2}$。DCR为分解策略的奖励提供了更优的估计，从而提升了统一训练中的稳定性和收敛速度。

UDC采用REINFORCE算法[44]来训练分解策略（损失为${\mathcal{L}}_d$）和求解策略（求解步骤的损失为${\mathcal{L}}_{c1}$，重组步骤的损失为${\mathcal{L}}_{c2}$）。训练分解策略时的基线是$\alpha$个初始解x0i,i∈{1,…,α}\boxed{x}_0^i, i \in \{1, \ldots, \alpha\}x​0i​,i∈{1,…,α}的平均奖励，训练求解策略时的基线是$\beta$个采样子解的平均值。单个实例$\mathcal{G}$上损失函数的梯度计算如下：

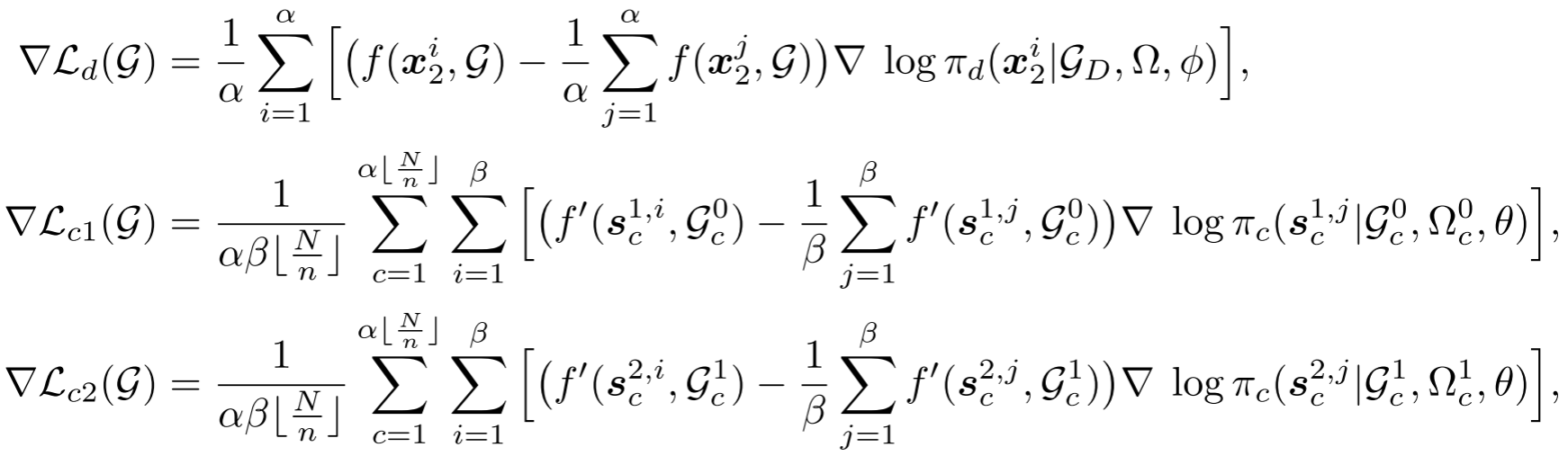
其中{x21,…,x2α}\{\boxed{x}_2^1, \ldots, \boxed{x}_2^\alpha\}{x​21​,…,x​2α​}表示$\alpha$个采样解。在第一个求解阶段中，基于{x01,…,x0α}\{\boxed{x}_0^1, \ldots, \boxed{x}_0^\alpha\}{x​01​,…,x​0α​}生成了$\alpha \lfloor \frac{N}{n}\rfloor$个子问题Gc0,c∈{1,…,⌊Nn⌋,…,α⌊Nn⌋}\mathcal{G}_c^0, c \in \{1, \ldots, \lfloor \frac{N}{n} \rfloor, \ldots, \alpha \lfloor \frac{N}{n} \rfloor\}Gc0​,c∈{1,…,⌊nN​⌋,…,α⌊nN​⌋}，这些子问题带有约束${\Omega }_c^0$。$\alpha \lfloor \frac{N}{n}\rfloor$可视为子问题的批量大小，Gc1,Ωc1,c∈{1,…,α⌊Nn⌋}\mathcal{G}_c^1, \Omega_c^1, c \in \{1, \ldots, \alpha \lfloor \frac{N}{n} \rfloor\}Gc1​,Ωc1​,c∈{1,…,α⌊nN​⌋}是第二个求解阶段中的子问题和约束。针对子问题Gc0,Gc1,c∈{1,…,α⌊Nn⌋}\mathcal{G}_c^0, \mathcal{G}_c^1, c \in \{1, \ldots, \alpha \lfloor \frac{N}{n} \rfloor\}Gc0​,Gc1​,c∈{1,…,α⌊nN​⌋}的$\beta$个采样子解记为{sc1,i,…,sc1,β},{sc2,i,…,sc2,β}\{\boxed{s}_c^{1,i}, \ldots, \boxed{s}_c^{1,\beta}\}, \{\boxed{s}_c^{2,i}, \ldots, \boxed{s}_c^{2,\beta}\}{s​c1,i​,…,s​c1,β​},{s​c2,i​,…,s​c2,β​}。

3.3 应用：在通用组合优化问题中的适用性

本小节讨论UDC在各类组合优化（CO）问题中的适用性。现有大多数神经分治方法依赖问题特定设计，因此仅适用于有限的组合优化问题。UDC在整个求解过程中不使用启发式算法或问题特定设计，因此可应用于满足以下三个条件的通用离线组合优化问题：

• 目标函数仅包含可分解的聚合函数（即不含Rank或Top-k类函数）；
• 初始解和子解的合法性可通过可行性掩码保证；
• 分解后的子问题的解不总是唯一的。

对于第二个条件，所提出的UDC在一些复杂组合优化问题上不适用——这些问题的解无法通过自回归求解过程保证合法性（例如带时间窗的旅行商问题（TSPTW））。对于第三个条件，在某些组合优化问题上（如稠密图上的最大独立集（MIS）问题或作业调度问题），子问题的解已被唯一确定，因此求解阶段将无效。

4 Experiment

为了验证UDC在一般CO问题中的适用性，我们对满足3.3节中提出的条件的10个组合优化问题（包括TSP、CVRP、KP、MIS、ATSP、Orienteering problem （OP）、PCTSP、Stochastic PCTSP （SPCTSP）、Open VRP （OVRP）和min-max多智能体TSP (min-max mTSP)）进行了UDC评价。 这些问题的详细表述见附录B。

通过使用轻量级网络划分策略，UDC可以直接在大规模CO实例（例如，TSP500和tsp1000）上进行训练。 为了学习更多与尺度无关的特征，我们在训练中采用变大小训练方案[45,46]，每个CO问题只训练一个UDC模型。 Adam优化器[47]用于所有涉及的CO问题，每个CO问题的详细超参数在附录D.1中提供。 大多数训练任务可以在10天内完成单个NVIDIA Tesla V100S GPU。 本文将提出的UDC与先进的启发式算法和现有的大规模CO问题的神经解算器进行了比较，包括经典解算器（LKH [48], EA4OP [49], ORTools[50]），基于单阶段ls的子路径解算器（BQ [14], LEHD[8]），基于单阶段rl的构造解算器（AM [51], POMO[5], ELG [6], ICAM [16]， MDAM[52]等），基于热图的解算器（DIMES [35]， DIFUSCO[39]等）和神经分治方法(GLOP [13], TAM [12], H-TSP[20]， 等)。 所有基线方法的实现细节和设置见附录G。

实现
通过为分解策略采用轻量级网络，UDC可直接在大规模组合优化（CO）实例（如TSP500、TSP1000）上训练。为学习更具尺度无关性的特征，我们在训练中采用变尺寸训练方案[45,46]，且针对每个组合优化问题仅训练一个UDC模型。所有涉及的组合优化问题均采用Adam优化器[47]，每个问题的详细超参数见附录D.1。大多数训练任务可在单块NVIDIA Tesla V100S GPU上于10天内完成。

基线
本文将所提UDC与大规模组合优化问题的先进启发式算法和现有神经求解器进行对比，涵盖以下类别：

• 经典求解器：LKH [48]、EA4OP [49]、OR-Tools [50]；
• 单阶段基于监督学习（SL）的子路径求解器：BQ [14]、LEHD [8]；
• 单阶段基于强化学习（RL）的构造性求解器：AM [51]、POMO [5]、ELG [6]、ICAM [16]、MDAM [52]等；
• 基于热图的求解器：DIMES [35]、DIFUSCO [39]等；
• 神经分治方法：GLOP [13]、TAM [12]、H-TSP [20]等。

所有基线方法的实现细节和设置见附录G。

500节点至2000节点实例的结果
我们首先考察UDC模型在500节点到2000节点规模的大规模组合优化问题上的性能。单阶段基于SL的构造性方法[16]和单阶段子路径求解器[8]无法在该规模下直接训练，因此我们报告这些基线在其最大可用规模下训练的模型结果。

对于UDC，我们不仅提供贪心结果（UDC-$x_2$），还提供执行更多求解阶段后的结果（即50次和250次阶段，记为UDC-$x_{50}$、UDC-$x_{250}$）。在贪心解之后的后续求解阶段中，子问题分解的起始点不再固定为$\frac{n}{2}$，而是从Uniform$(0,n)$中采样。为获得更优性能，我们对TSP和CVRP采样$\alpha =50$个初始解$x_0$。

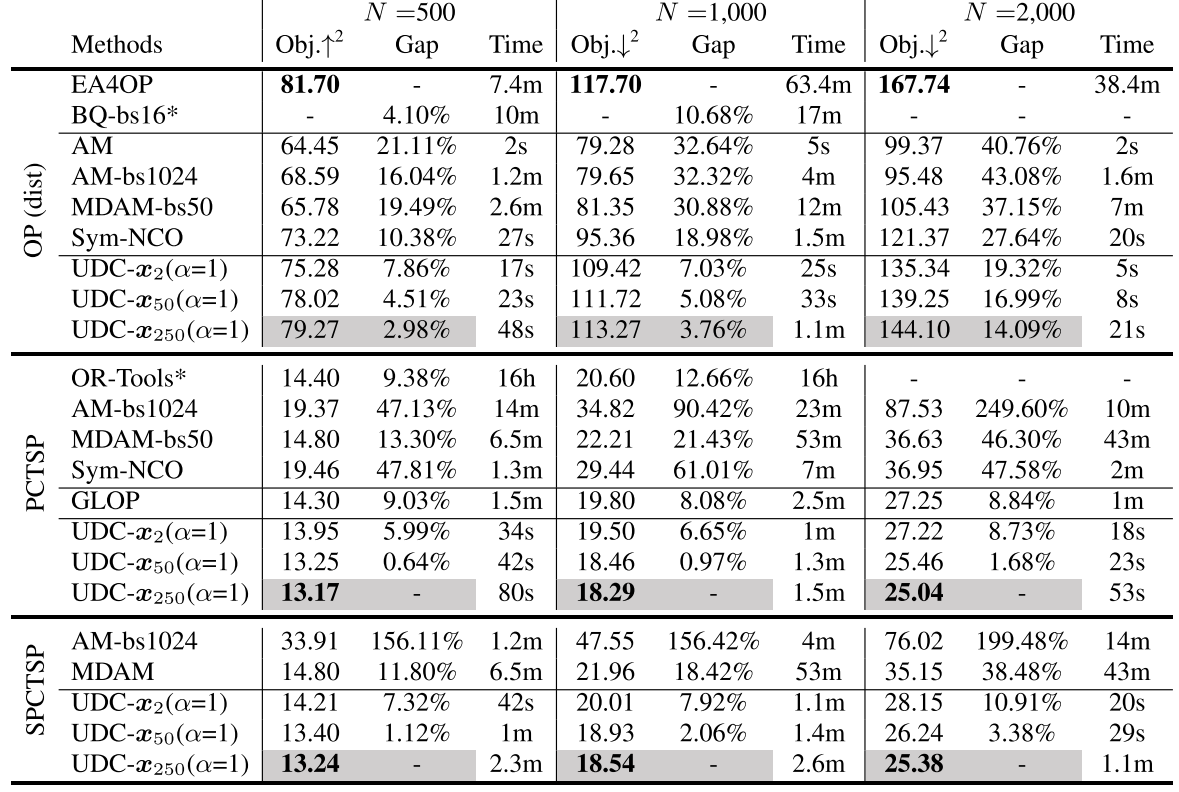
TSP和CVRP的对比结果见表2，定向越野问题（OP）、带奖励收集TSP（PCTSP）和随机PCTSP（SPCTSP）的结果见表4。UDC展现出通用适用性，在涉及的所有五类组合优化问题中均表现出持续的竞争力；经过多轮求解阶段后，UDC可获得显著更优的结果。

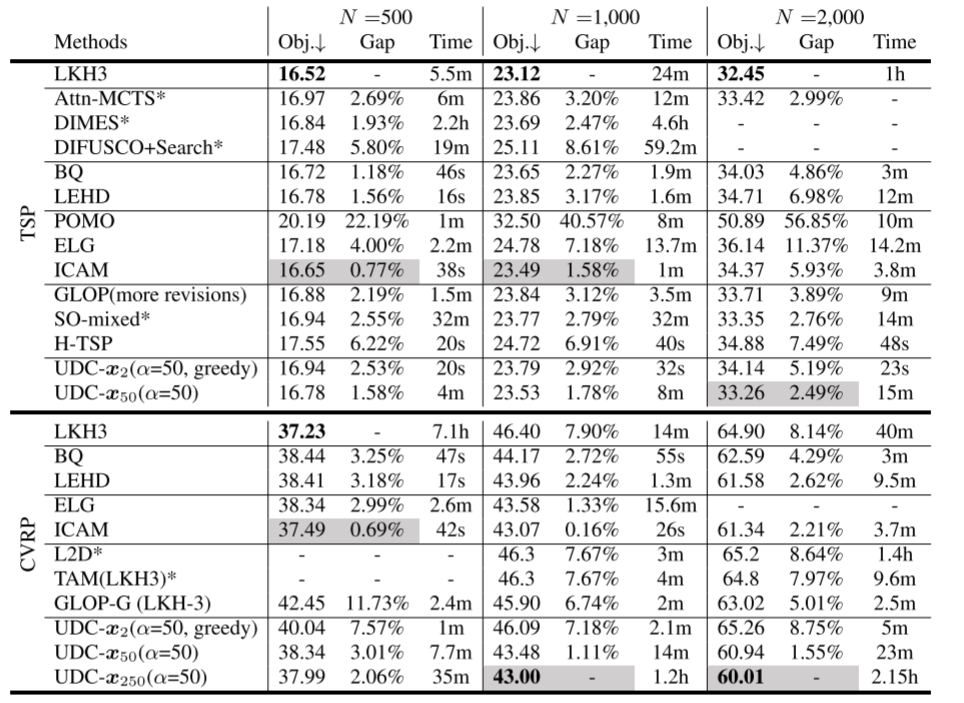
UDC变体在PCTSP、SPCTSP、CVRP1000和CVRP2000中表现最佳，且在大多数涉及的组合优化问题中是最优的基于学习的方法。UDC-$x_{250}(\alpha =1)$在OP、PCTSP和SPCTSP中展现出广泛的高效性。与子路径求解器BQ [14]和LEHD [8]相比，UDC变体在TSP1000、TSP2000、CVRP和OP上表现更具竞争力。带有8种增强的基于RL的构造性求解器ICAM [16]在TSP500、TSP1000和CVRP500（即相对较小规模）上表现出色，但UDC变体在其他测试集上展现出更优的效果和效率。

此外，与现有神经分治方法GLOP [13]、H-TSP [20]和TAM(LKH3) [12]相比，UDC在无启发式设计的情况下性能显著更优，这初步表明了神经分治方法统一训练方案的重要性。