Floyd算法
在前面的的几期中,我们已经讲过了利用广度优先算法和Dijkstra算法,这两个算法都是以单源为主,其中Dijkstra算法可以计算两个顶点间的最短路径,一直遍历顶点即可,但比较麻烦,不会有人去这么做,今天给大家再来介绍一直可以计算两点间的最短路径----Floyd算法
Floyd使用动态规划思想,将问题的求解分为多个阶段
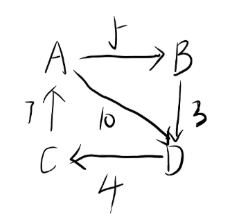
例如上述图
初始状态:不以其他点为中转点的最短路径是多少
第一步:以A为中转点的最短路径是多少
第二步:以B为中转点的最短路径是多少
依次类推.....
除了邻接矩阵外我们还有创建一个数组path[MAX]
其中在邻接矩阵中我们放置原本有向图的路径,在path[MAX]中放置两个点之间的中转点,初始值都为-1
核心代码:
if(A[i][j] > A[i][k] + A[k][j]) //用来判断当前的路径长度是否大于中转后的长度
{
A[i][j] = A[i][k] + A[k][j]; //如果大于的话则交换
path[i][j] = k;//设置中转点
}
具体代码:
//邻接矩阵的构建
#include<stdio.h>
#include<stdbool.h>
#include<limits.h>
#define VertexNum 4 //假设是4个顶点组成的有向图
typedef struct
{
char Ver[VertexNum];//顶点的集合
int Edge[VertexNum][VertexNum];//邻接矩阵边表,bool类型只存放0和1
int vexnum;//顶点数
}MGraph;
//初始化邻接矩阵
void InitGraph(MGraph* M)
{
M->vexnum = 0;//初始化为0
int i, j;
//初始化顶点
for (i = 0; i < VertexNum; i++)
{
M->Ver[i] = '\0';
}
//初始化邻接矩阵
for (i = 0; i < VertexNum; i++)
{
for (j = 0; j < VertexNum; j++)
{
M->Edge[i][j] = 0;//初始化矩阵全为零
}
}
return;
}
//创建顶点
bool EnVertex(MGraph* M)
{
if (M->vexnum >= VertexNum)
return false;//空间已满
int i = 0;
while (i < VertexNum)
{
M->Ver[i] = 'A' + i;
M->vexnum++;
i++;
}
return true;
}
//创建边
bool EnEdge(MGraph* M)
{
if (M->vexnum <= 1)
return false;//非图或者只有一个顶点无法创建边
//创建A的边
M->Edge[0][1] = 5;
M->Edge[0][2] = 99999;
M->Edge[0][3] = 10;
//创建B的边
M->Edge[1][0] = 99999;
M->Edge[1][2] = 99999;
M->Edge[1][3] = 3;
//创建C的边
M->Edge[2][0] = 7;
M->Edge[2][1] = 99999;
M->Edge[2][3] = 99999;
//创建D的边
M->Edge[3][0] = 99999;
M->Edge[3][1] = 99999;
M->Edge[3][2] = 4;
return true;
}
//Floyd算法
void Floyd(MGraph* M, int path[VertexNum][VertexNum])
{
int k, i, j;
for (k = 0; k < VertexNum; k++)
{
for (i = 0; i < VertexNum; i++)
{
for (j = 0; j < VertexNum; j++)
{
if (M->Edge[i][j] > M->Edge[i][k] + M->Edge[k][j])//以k为中转点大于原来的路径
{
M->Edge[i][j] = M->Edge[i][k] + M->Edge[k][j];
path[i][j] = k; //保留中转点
}
}
}
}
}
void PrintF(MGraph G,int path[VertexNum][VertexNum])
{
int i, j;
for (i = 0; i < VertexNum; i++)
{
for (j = 0; j < VertexNum; j++)
printf("%d ", G.Edge[i][j]);
printf("\n");
}
for (i = 0; i < VertexNum; i++)
{
for (j = 0; j < VertexNum; j++)
printf("%d ", path[i][j]);
printf("\n");
}
}
int main()
{
MGraph M;//定义一个指向图的变量
InitGraph(&M);//初始化图
EnVertex(&M);//插入顶点
EnEdge(&M);//创建边
int path[VertexNum][VertexNum] = {0};
int i;
int j;
for (i = 0; i < VertexNum; i++)//path的初值都为-1,表示没有中转点
for (j = 0; j < VertexNum; j++)
path[i][j] = -1;
Floyd(&M, path);
PrintF(M,path);
return 0;
}
时间复杂度O(n³)
空间复杂度O(n²)
注意:这个代码一开始在设置两个顶点之间没有直接路径的时候,采用了99999,这个其实没有其他含义就是表示的足够大,在编写的时候直接设置足够大就行,但注意<limits.h>库中为我们定义了INT_MAX的最大值,但跟我的实验过程中发现,当使用INT_MAX的时候,如果INT_MAX再相加的话,就会产生溢出的现象,我们的编写代码的时候要注意。
