数据结构(14)
目录
一、最小生成树(MST)
1、最小生成树的核心定义与性质
(1)定义
(2)关键性质
2、构造最小生成树的经典算法
(1)Kruskal 算法(“加边法”)
(2)Prim 算法(“加点法”)
3、示例说明(对比两种算法)
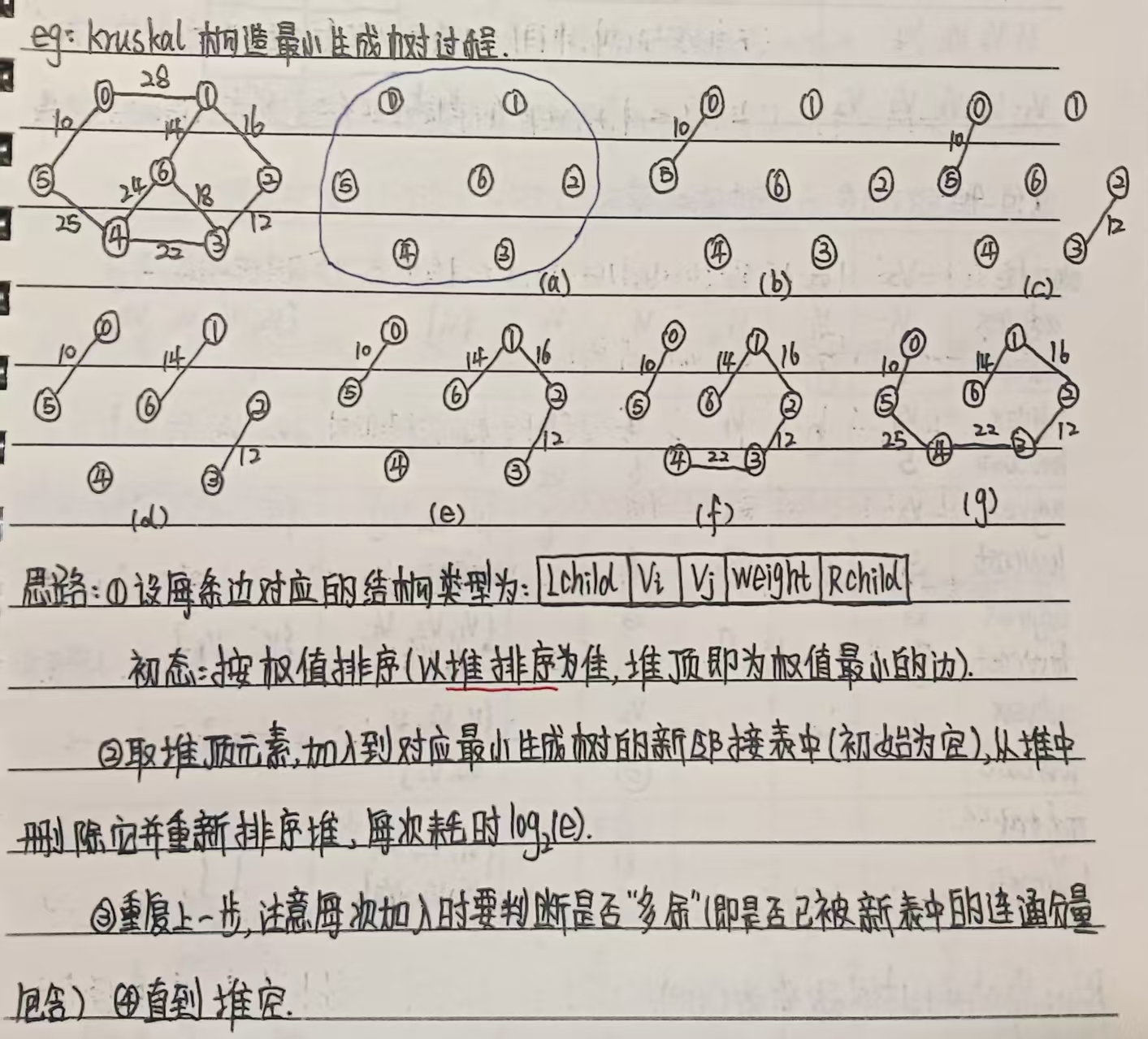
(1)Kruskal 算法过程
(2)Prim 算法过程(从顶点 0 出发)
4、适用场景
二、普利姆算法(prime)
三、克鲁斯卡尔算法(kruskal)
一、最小生成树(MST)
(1)在网络的多个生成树中,寻找一个各边权值之和最小的生成树
(2)使用不同的遍历图的方法,可以得到不同的生成树;从不同的顶点出发也可以得到不同的生成树
(3)按照生成树的定义,n 个顶点的连通网络的生成树有 n 个顶点,n-1 条边
(4)准则:
① 必须只使用该网络中的各边来构造最小生成树
② 必须使用且仅使用 n-1 条边来联络网络中的 n 个顶点
③ 不能使用产生回路的边
(5)MST性质:若 U 集是 V 的一个非空子集,若 是一条最小权值的边,其中
,
,则
必在MST上
最小生成树(Minimum Spanning Tree, MST)是针对带权连通无向图的一种特殊生成树,其核心特点是:包含图中所有顶点,且所有边的权重之和(总权重)在所有可能的生成树中最小。MST 既保留了原图的连通性(作为生成树的基本属性),又通过最小化总权重,在网络设计、路径规划等场景中具有重要实用价值(如最小成本布线、最短管道铺设等)。
1、最小生成树的核心定义与性质
(1)定义
对于一个带权连通无向图 G=(V,E)(V 为顶点集,E 为带权边集),其最小生成树是满足以下条件的子图 T:
- T 包含 G 中所有顶点(VT=V)。
- T 是连通的,且无环(是一棵生成树)。
- T 中所有边的权重之和 ∑(w(e)) 是所有可能生成树中最小的。
(2)关键性质
- 边数固定:含 n 个顶点的 MST 有且仅有 n−1 条边(生成树的基本性质)。
- 唯一性:若图中所有边的权重互不相同,则 MST 是唯一的;若存在相同权重的边,可能有多个 MST(但总权重相同)。
- 割边性质:在图中任意划分顶点为两个子集(割集),连接两个子集的所有边中,权重最小的边一定属于 MST(用于证明 MST 算法的正确性)。
- 回路性质:图中任意回路,回路中权重最大的边一定不属于 MST(若包含该边,删除后可形成总权重更小的生成树)。
2、构造最小生成树的经典算法
构造 MST 的核心思想是 “在保持连通且无环的前提下,选择权重最小的边”,两大经典算法分别是Kruskal 算法和Prim 算法。
(1)Kruskal 算法(“加边法”)
- 核心思路:按边的权重从小到大排序,依次选择边加入 MST,若加入后不形成环,则保留该边;直到加入 n−1 条边为止。
- 关键步骤:
- 对所有边按权重从小到大排序。
- 初始化 MST 为 “空集”,顶点各自独立(不连通)。
- 按排序顺序遍历边:若边的两个顶点分属不同的连通分量(加入后无环),则将该边加入 MST,并合并两个连通分量。
- 重复步骤 3,直至 MST 包含 n−1 条边。
- 环检测工具:并查集(Union-Find),高效判断两顶点是否连通及合并连通分量(时间复杂度接近 O(1))。
- 时间复杂度:O(eloge)(主要耗时在边的排序,e 为边数),适合稀疏图(边数少)。
(2)Prim 算法(“加点法”)
- 核心思路:从任意顶点出发,逐步将 “与当前 MST 连通且权重最小的顶点” 纳入 MST,直到包含所有顶点。
- 关键步骤:
- 选择起始顶点 v0,将其加入 MST,标记为 “已访问”。
- 记录所有未访问顶点到 MST 的 “最小距离”(即该顶点与 MST 中某顶点的边的最小权重)。
- 选择 “最小距离” 最小的未访问顶点 u,将其加入 MST,并更新其他未访问顶点到 MST 的 “最小距离”(若通过 u 连接的边权重更小)。
- 重复步骤 2-3,直至所有顶点均加入 MST(共加入 n−1 条边)。
- 优化工具:优先队列(如最小堆),高效获取 “最小距离” 的顶点(时间复杂度 O(logn))。
- 时间复杂度:O(elogn)(n 为顶点数),适合稠密图(边数多)。
3、示例说明(对比两种算法)
假设有带权连通无向图 G:顶点 V={0,1,2,3},边及权重:(0,1,4),(0,2,2),(0,3,6),(1,3,1),(2,3,3)
(1)Kruskal 算法过程
- 边排序:(1,3,1)<(0,2,2)<(2,3,3)<(0,1,4)<(0,3,6)。
- 选边:
- 加入 (1,3,1)(1 和 3 连通)。
- 加入 (0,2,2)(0 和 2 连通)。
- 加入 (2,3,3)(2 与 3 连通,此时 0-2-3-1 全连通,共 3 条边,停止)。
- MST 总权重:1+2+3=6。
(2)Prim 算法过程(从顶点 0 出发)
- 初始:MST = {0},距离:1→4,2→2,3→6。
- 选距离最小的 2(距离 2),加入 MST,更新距离:3→min (6, 3) = 3。
- 选距离最小的 3(距离 3),加入 MST,更新距离:1→min (4, 1) = 1。
- 选距离最小的 1(距离 1),加入 MST,共 3 条边,停止。
- MST 总权重:2+3+1=6。
4、适用场景
MST 的核心价值是 “以最小成本保持连通”,典型应用包括:
- 网络布线:在多个建筑物间铺设电缆,使总成本最低且所有建筑物连通。
- 交通规划:修建公路连接多个城市,总里程最短且确保城市间可互达。
- 电路设计:芯片中连接多个元件,导线总长度最小。
- 聚类分析:将相似数据点(顶点)按最小 “距离”(权重)聚为一类,形成连通子图。
二、普利姆算法(prime)
思路:将顶点归并,与边数无关,是用于稠密图
设:N=(V,E)是个连通图,另设U为最小生成树的顶点集,TE是最小生成树的边集
步骤:① 初始态:U={},(
),TE={ }
② 从E中选择定点分别属于U、V-U两个集合,且权值最小的边 ,将顶点
归并到集合U中,边
归并到TE中
③ 直到 U=V 为止,此时 TE 中必有 n-1 条边,T=(v,{TE}) 就是最小生成树
例题:
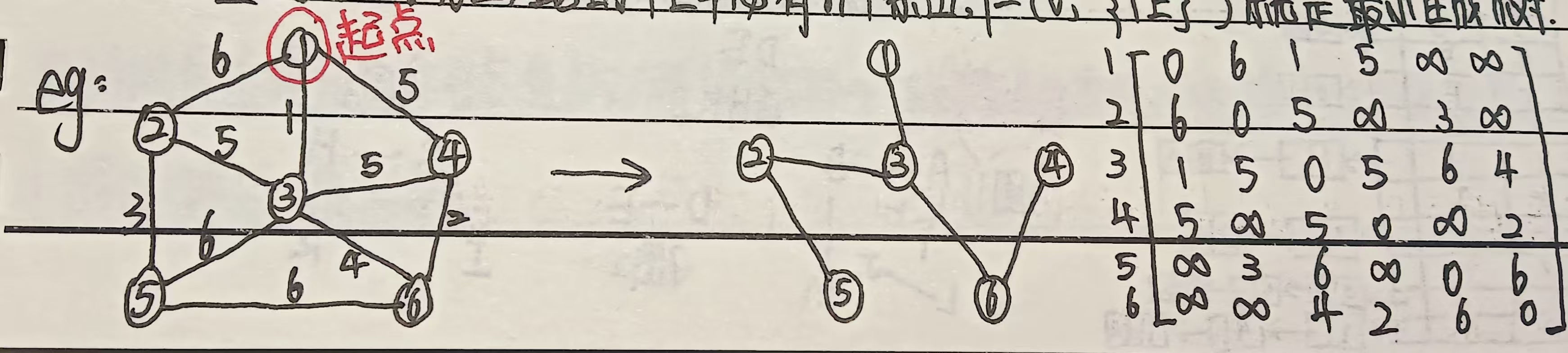
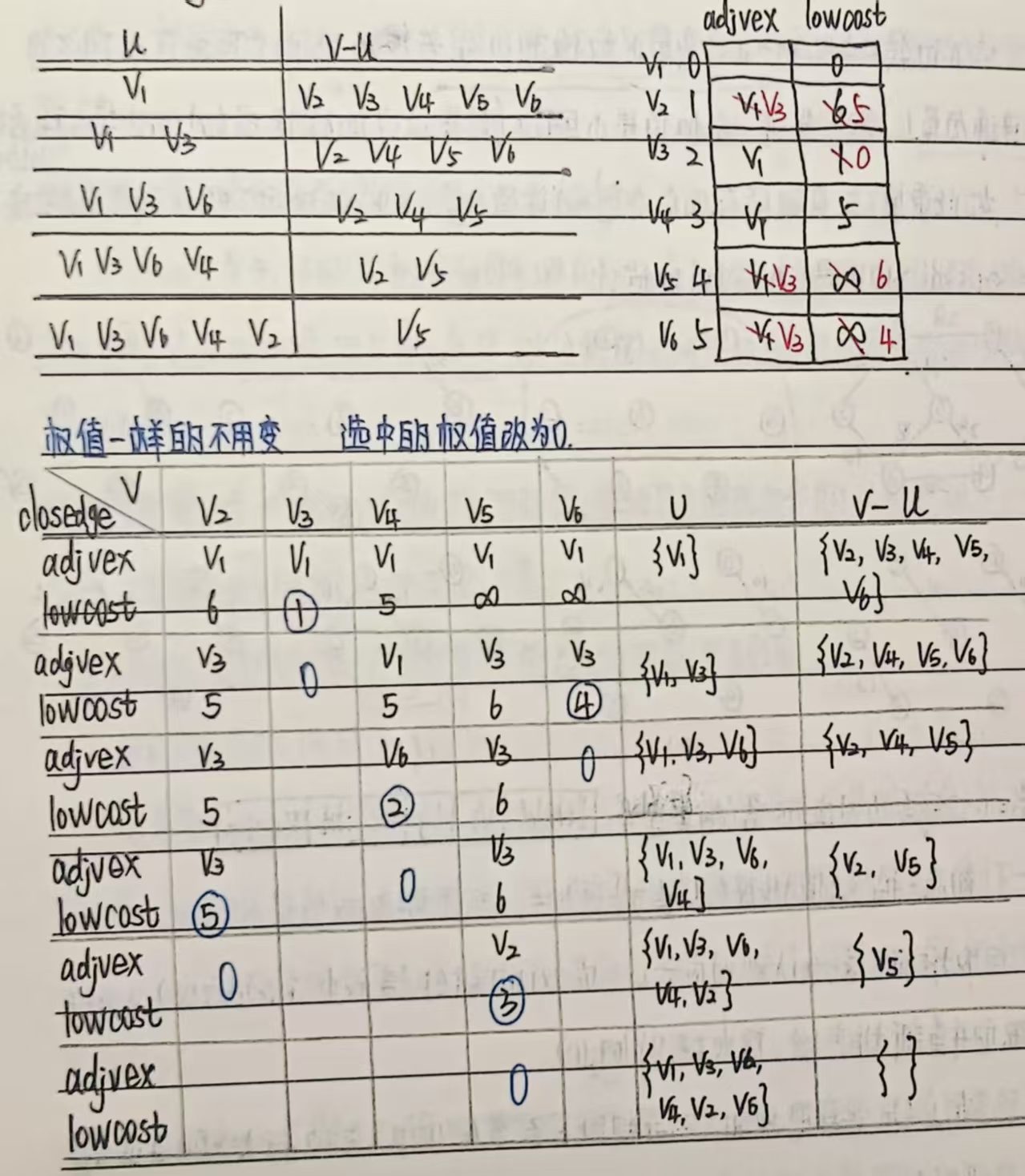
增设一辅助数组 Closedge[n]:
| adjvex | lowcost |
Closedge[n]:V-U 中顶点
adjvex: 在 U 中邻点 u
lowcost:u 与 之间对应的边权
要使:Closedge[n].lowcost= min(u,)
三、克鲁斯卡尔算法(kruskal)
思路:归并边,适合稀疏图——邻接表
设 N={V,E} 是有 n 个顶点的连通图
步骤:① 首先构造一个只有 n 个顶点,但没有边的非连通图T={V,},图中每个顶点自成一个连通分量
② 当边集 E 中选到一条具有最小权值的边时,若该边的两个顶点落在T 中不同的连通分量上,则将此边加入到生成树的边集合T中,否则将此边舍去,重新选择一条权值最小的边
③ 如此重复下去,直到所有顶点在同一个连通分量上为止。此时的 T 即为所求最小生成树
例题: