二叉树核心算法分类精讲:选择、遍历与结构关系
目录
- 前言
- 一、二叉树选择题
- 二、二叉树算法题
- 2.1 单值二叉树
- 2.2 相同的树
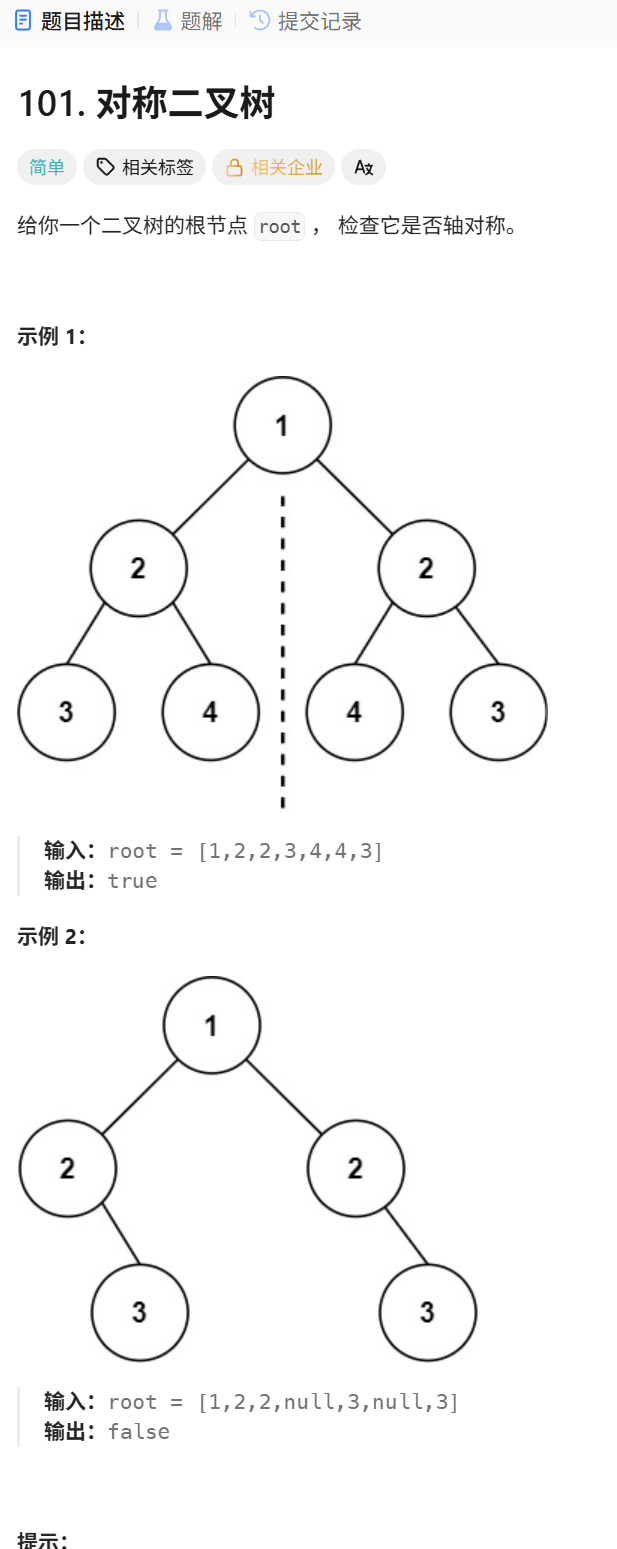
- 2.3 对称二叉树
- 2.4 另一棵树的子树
- 2.5 二叉树的前序遍历
- 2.6 二叉树的中序遍历
- 2.7 二叉树的后序遍历
- 2.8 二叉树的构建及遍历
- 结语


前言
大家好啊,我是云泽Q,欢迎阅读我的文章,一名热爱计算机技术的在校大学生,喜欢在课余时间做一些计算机技术的总结性文章,希望我的文章能为你解答困惑~
一、二叉树选择题
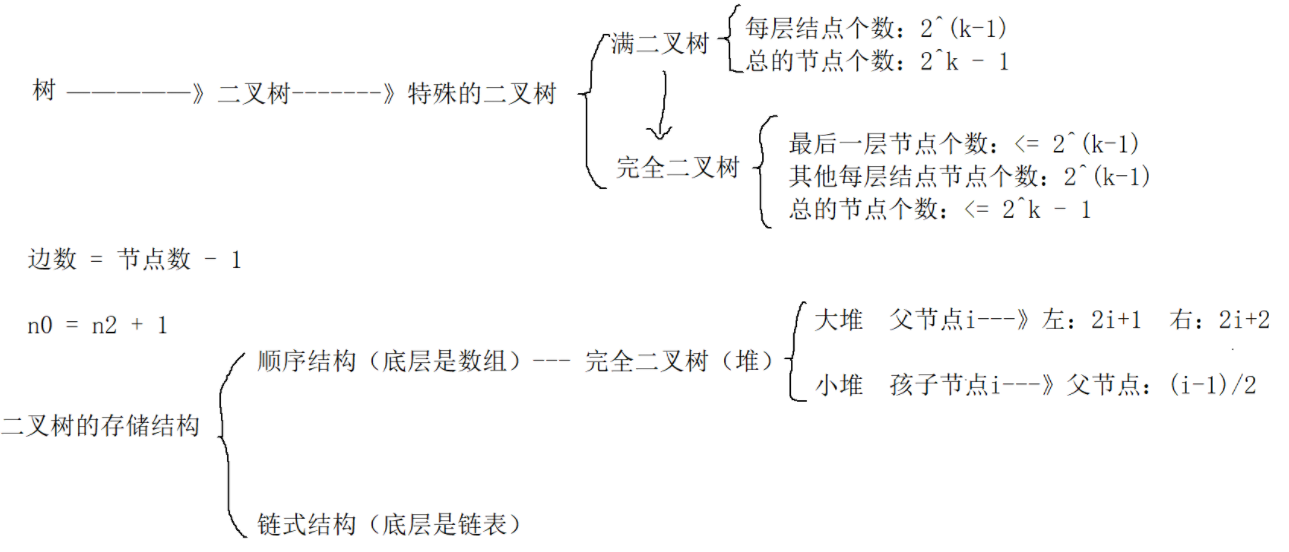
二叉树有一个性质:
- 对任何一棵二叉树,如果度为0,其叶结点个数为n0,度为2的分支,结点个数为n2,则有n0=n2+1
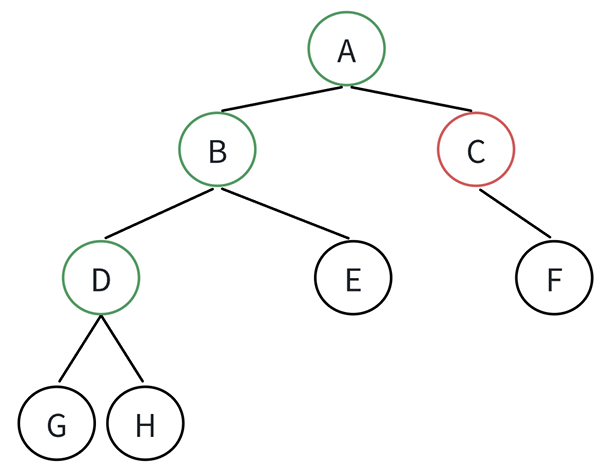
在该图中,用绿色标记度为2的结点,红色标记度为1的结点,黑色标记度为0的结点,二叉树的结点只有三种情况:度为0,1,2。这里认为度为0的节点总数是n0,度为2的结点个数总数为n2,度为1的节点总数是n1
树还有一个性质就是:边数 = 结点个数 - 1(两个结点用一条边相连)
结合图中就有了下面的公式:
边数 = n0 + n1 + n2 - 1
求边数还有一个公式:


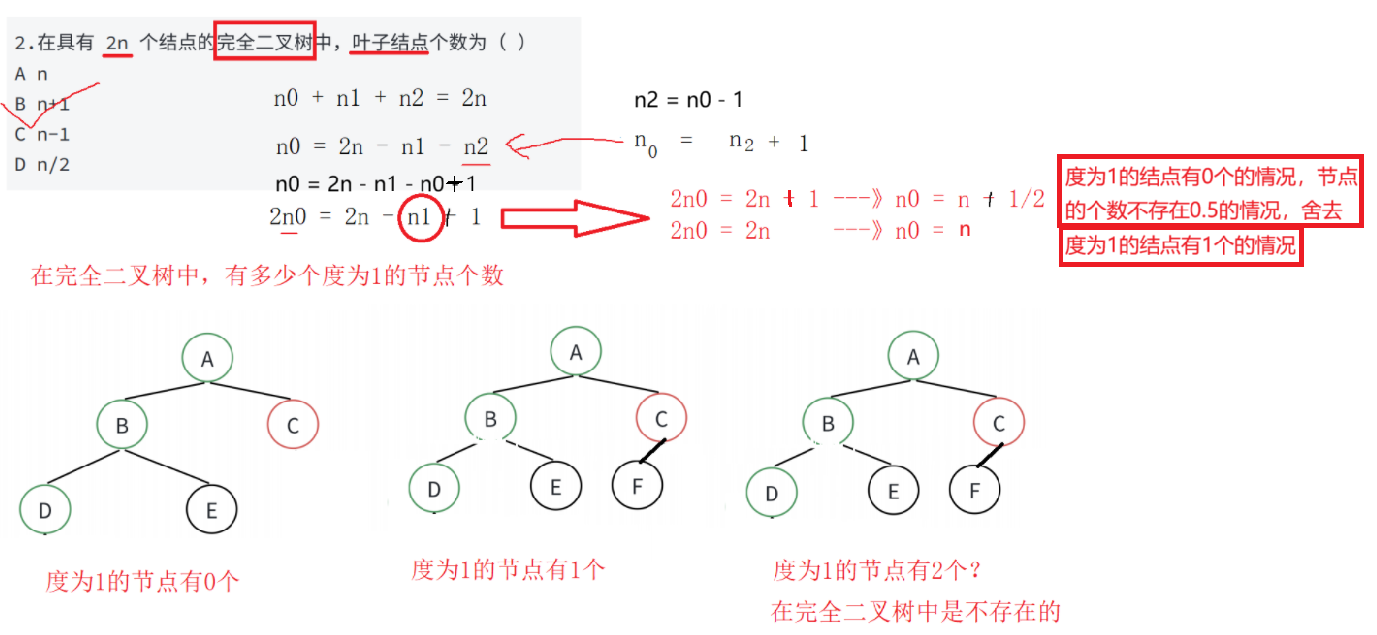
该题选A



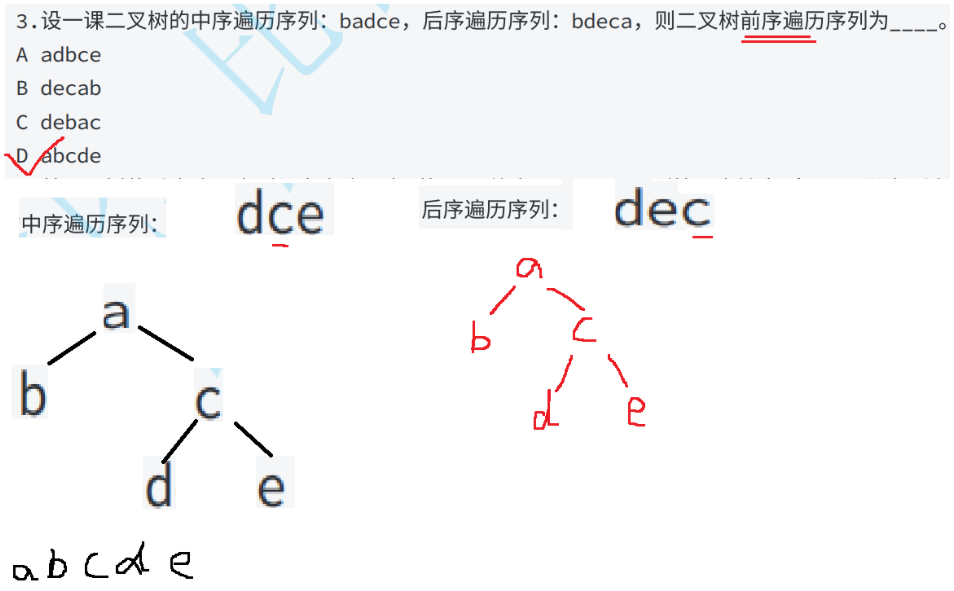
这题要先通过后序遍历找根节点(a),再通过中序遍历找左子树(b),最后通过中序遍历和后续遍历的右子树判断右子树的根节点(c),还原二叉树后再前序遍历,也可以找到一个节点直接删除一个节点,再判断剩余的节点

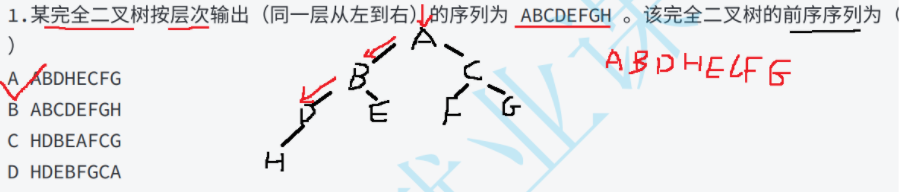
该题依旧按照前面的方法,从后序遍历就知道最后一个节点F是根节点,然后就把后序遍历和中序遍历中的F删了,由于中序遍历是左根右,在F左边的都是左子树,所以可以知道该二叉树没有右子树,左子树的根节点为E

再看中序遍历,E左边是左子树,右边是右子树,所以依旧没有左子树
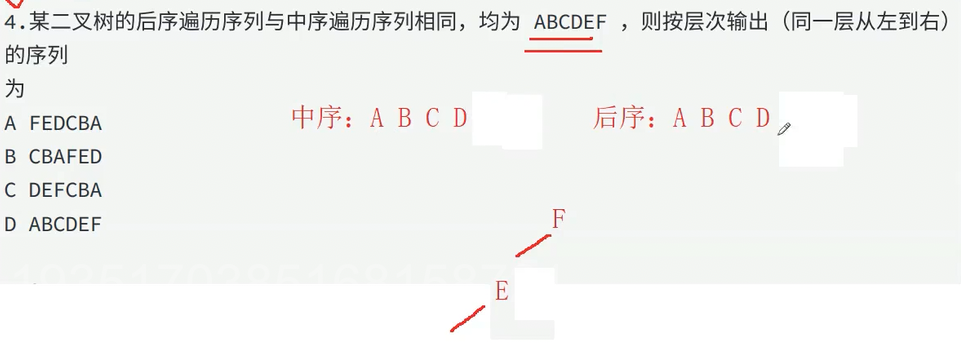
以此类推
二、二叉树算法题
2.1 单值二叉树
单值二叉树
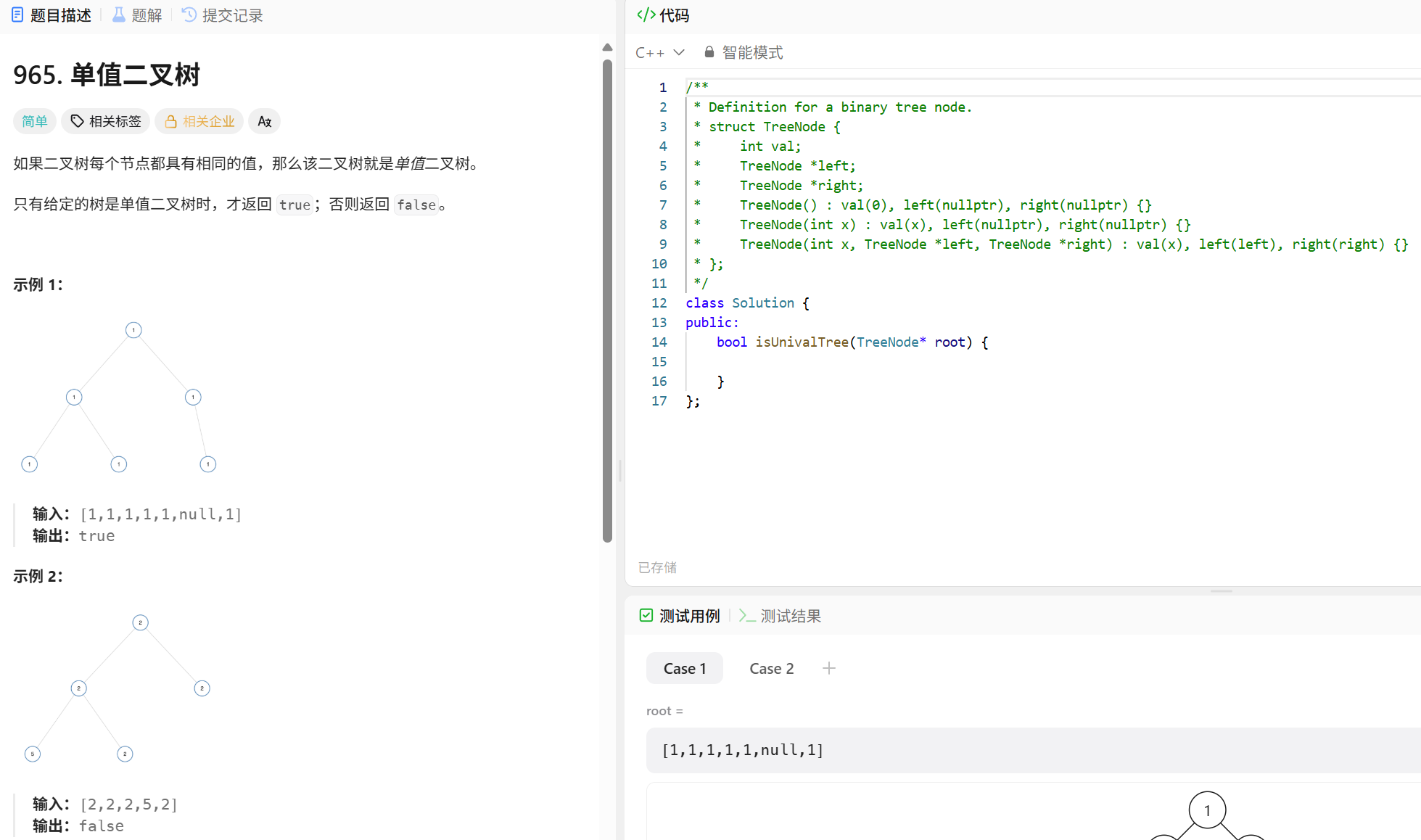
这里不用拿根节点和其所有孩子进行一一比较,如果当前根节点的值和左孩子相同,和右孩子也相同,说明左右孩子的值也是相同的,接下来继续拿左子树的根节点和其左右孩子相比较,右子树根节点和其左右孩子相比较,如果他们分别相同,那么就说明所有结点的值都相同

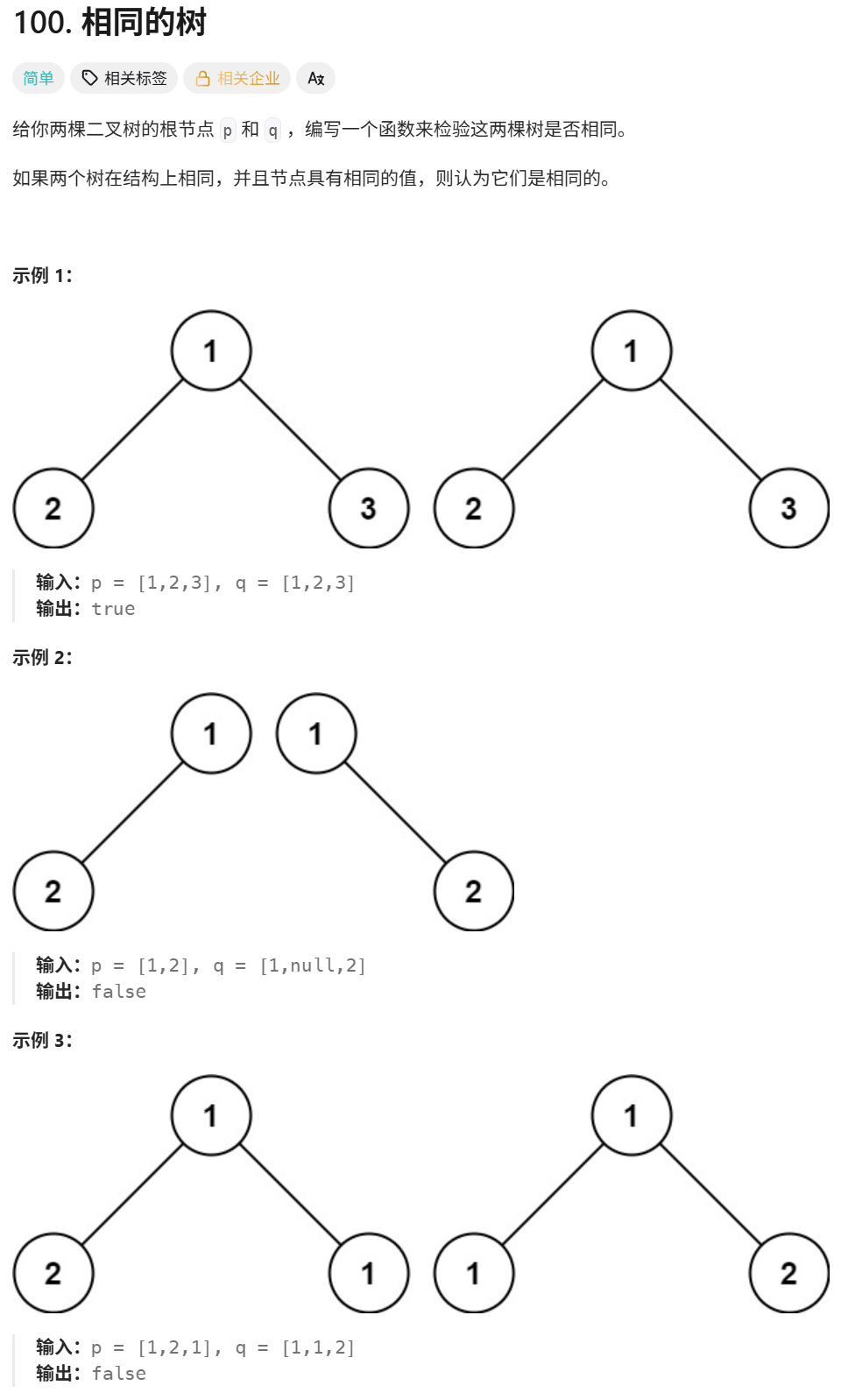
2.2 相同的树
相同的树
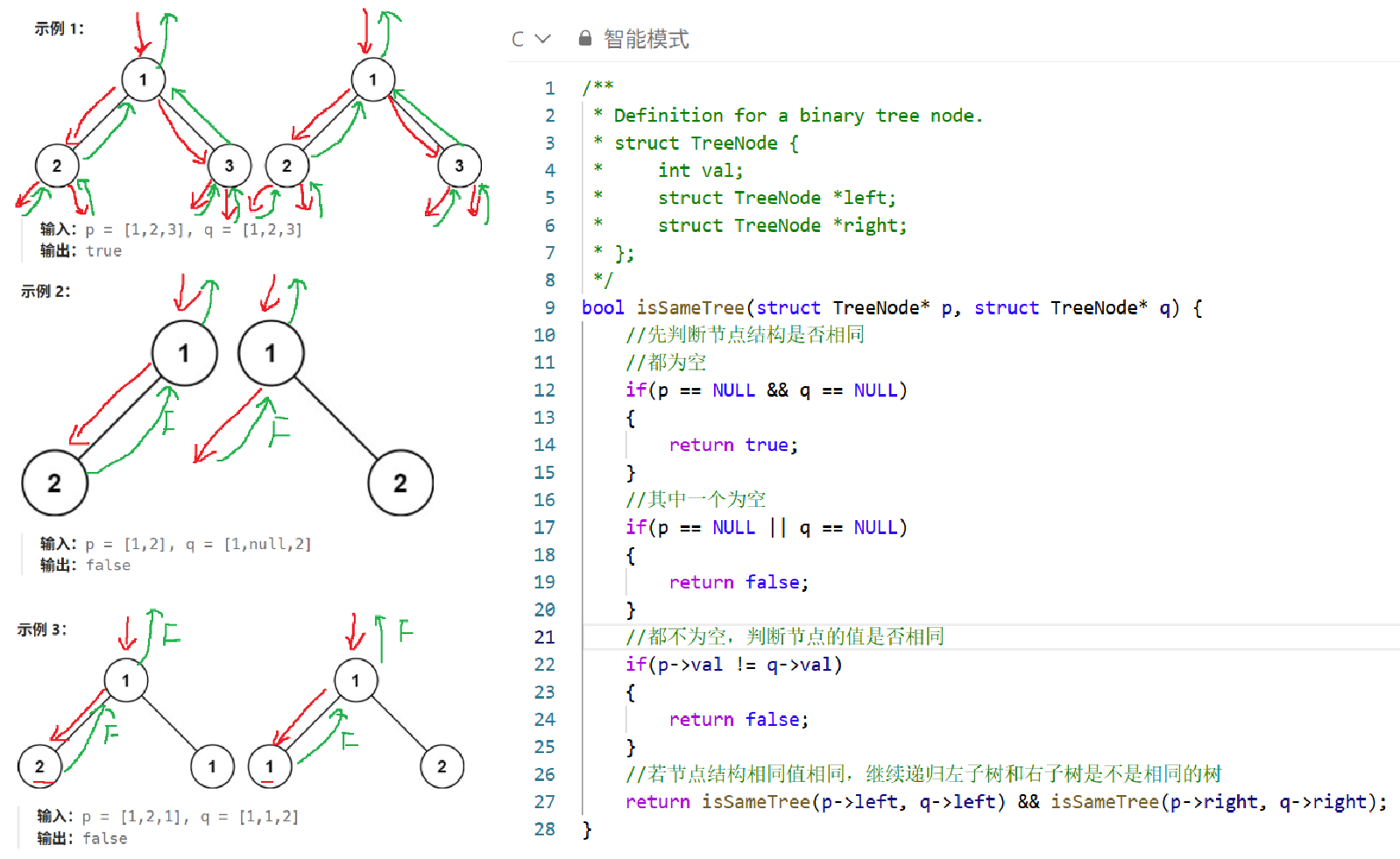
2.3 对称二叉树
对称二叉树
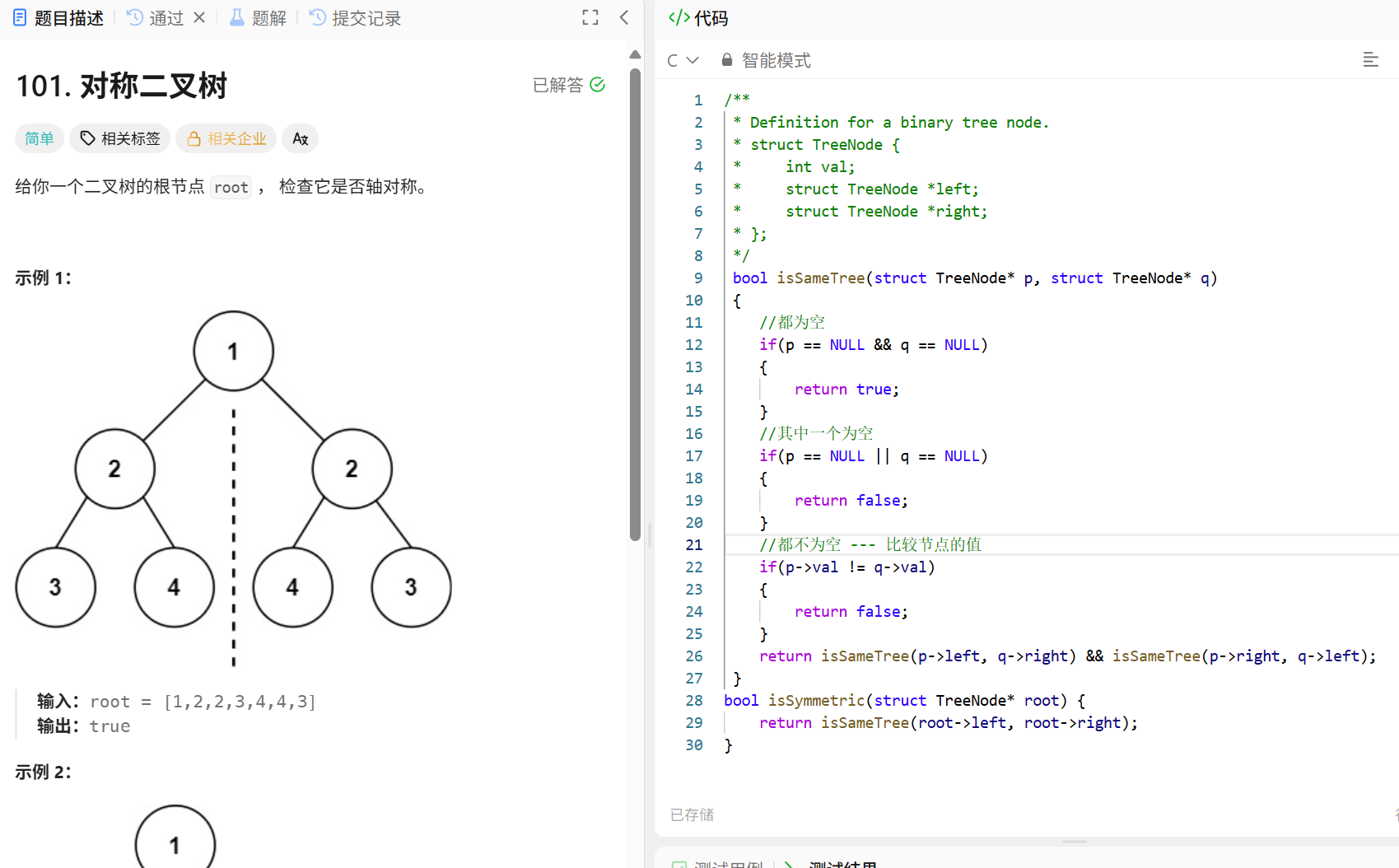
这里的比较和相同的树的区别就是,相同的树的比较是同时比较两个二叉树相同结构位置的节点。而这里对称比较是比较根结点(结构和值)之后,再递归一个树的左节点和另一个树的右节点是否相同
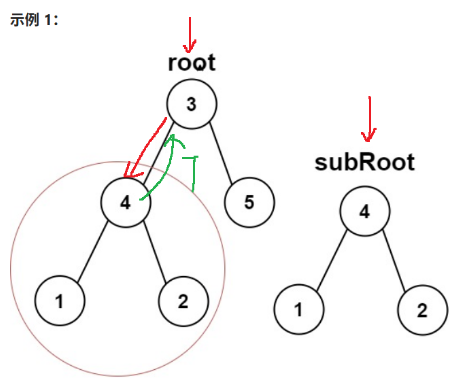
2.4 另一棵树的子树
另一棵树的子树
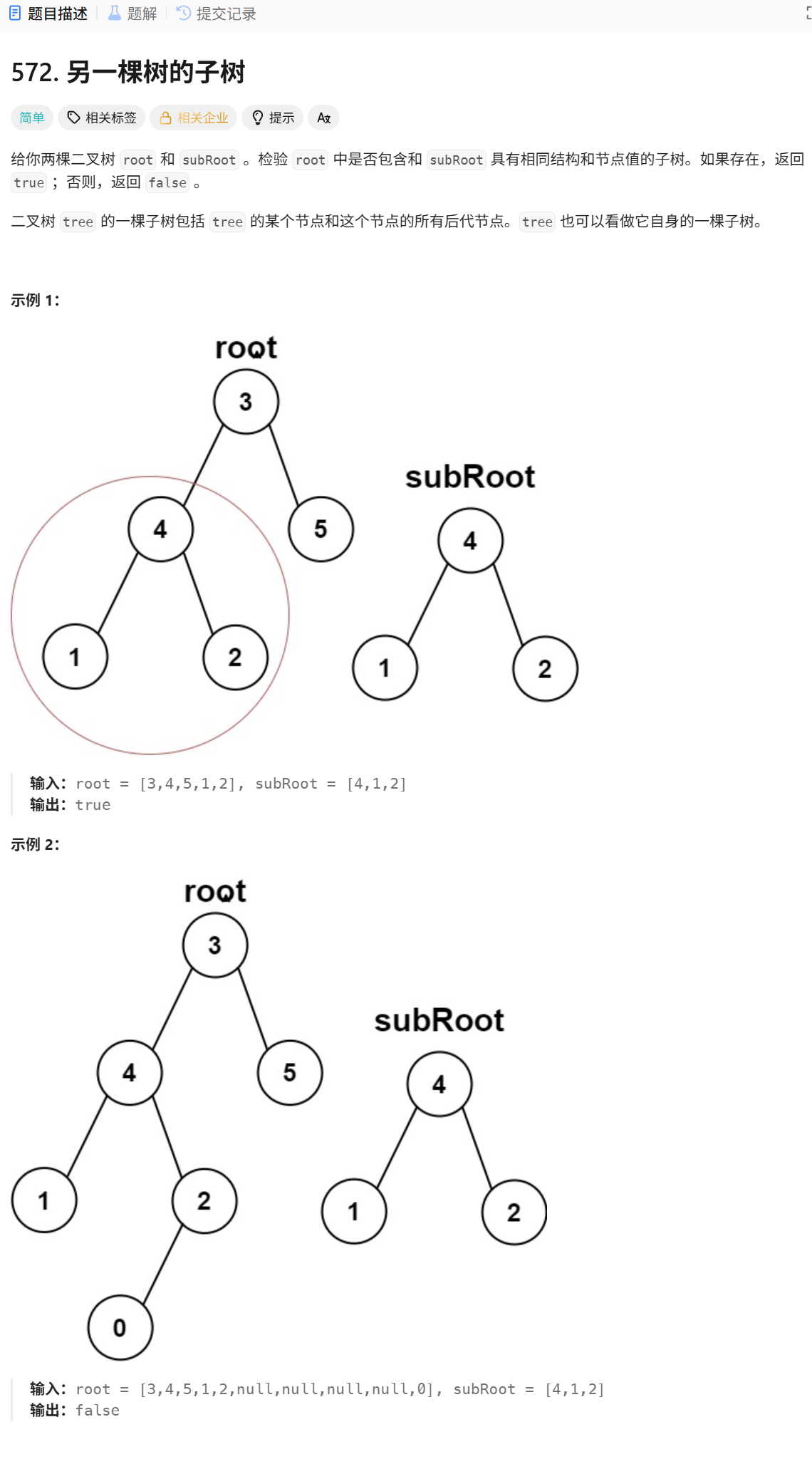
两个指针分别指向root和subRoot的根节点,都从根结点出发,先判断两棵树(整个root和subRoot)是不是相同的树,若不是便递归root的左子树(以4为根),判断4这个二叉树是不是和subRoot相同,若不相同再判断subRoot和root的右子树(5)是否相同,相同便直接return true
这里分析一下给的两个示例:
示例1:先用root的整个二叉树和subRoot比较,从两个二叉树的根节点出发,比较两棵树发现不是相同的树,便递归root的左子树(以4为根),发现以4为根的二叉树和subRoot是相同的,便直接return true
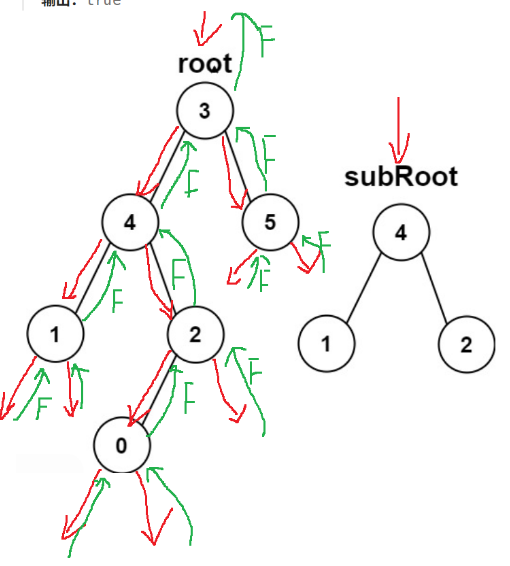
示例2:先用root的整个二叉树和subRoot比较,从两个二叉树的根节点出发,比较两棵树发现不是相同的树,便递归root的左子树(以4为根,4120),发现以4为根的二叉树和subRoot(412)是不同的。继续递归4的左子树(1),与subRoot不是相同的二叉树,再递归1的左右子树(为NULL),直接return false回到4这个二叉树中,4的左子树和subRoot不相同,继续递归4的右子树,4的右子树(2)不为空和subRoot比较,因为不相同继续递归2的左子树(0),0这个左子树不为空和subRoot比较不相等,继续递归0的左子树(NULL),其左右子树都为NULL,return false给2这个二叉树,2的左子树和subRoot不相同,递归2的右子树,2的右子树为NULL,直接return false给4这个二叉树,4此时左右子树和subRoot都不相同,便返回false给3这个二叉树。此时3这个二叉树左子树和subRoot不相同,递归其右子树(5)和subRoot比较,5和subRoot不是相同的树,继续递归5的左右子树(NULL),return false给5这个二叉树,说明5的左右子树和subRoot不是相同的树,继续返回false给3这个二叉树,3这棵二叉树左右子树和subRoot都不相同,说明subRoot就不是root的子树,return false
2.5 二叉树的前序遍历
二叉树的前序遍历
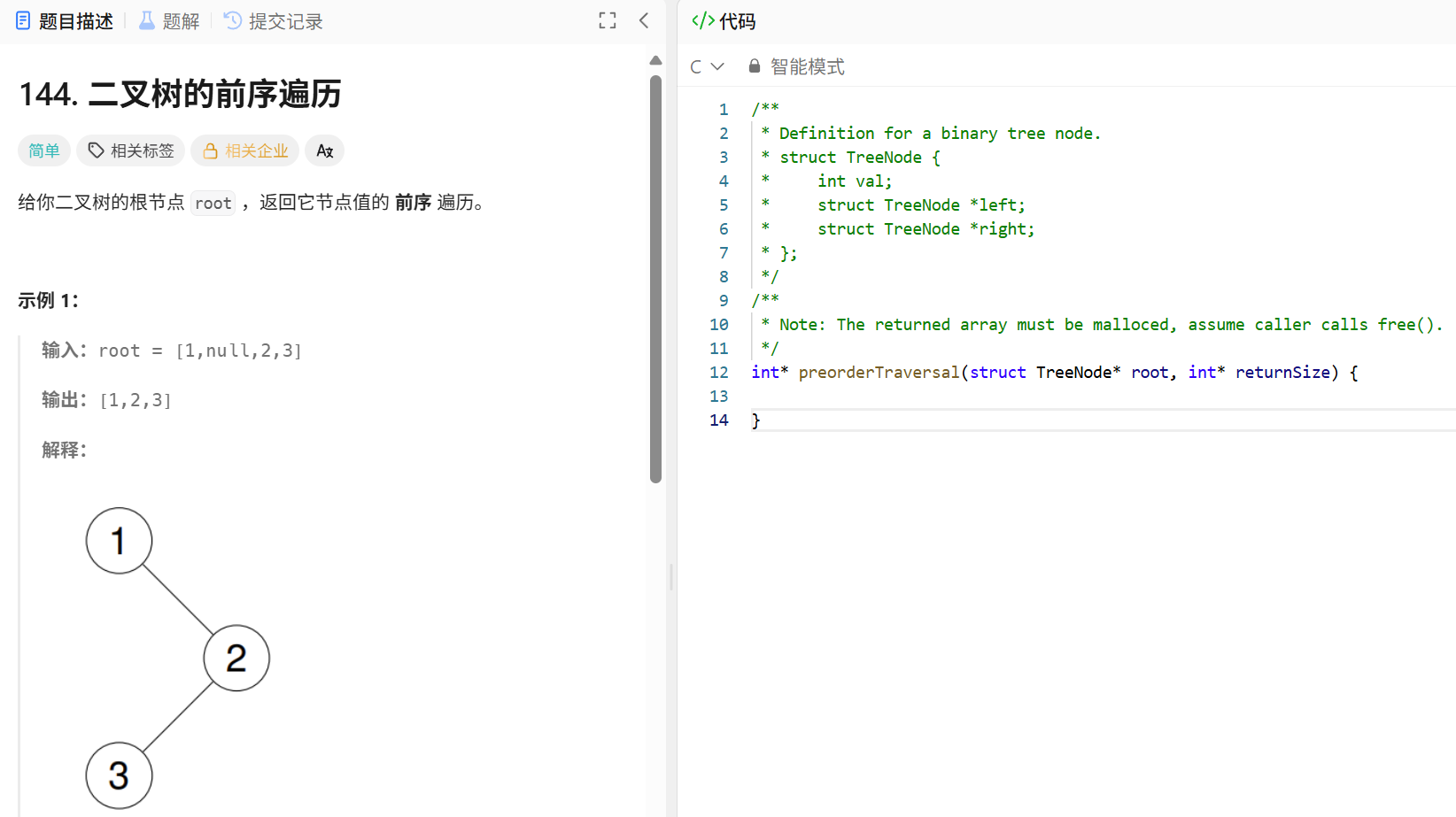
这里题目的描述给的比较少,只是Note中说要返回的数组必须是自己malloc的,也就是函数的返回值int* 是一个数组,数组的大小是要自己计算开辟的,前序遍历的结果要保存在数组当中
第二个参数returnSize返回数组的大小用了一个指针,若returnSize是一个确定的结果,就不用传地址了,传值就可以了,也就是说这里的returnSize也是一个不确定的值,需要自己去求,远程服务器最后根据方法的调用知道returnSize是多少
2.6 二叉树的中序遍历
二叉树的中序遍历

2.7 二叉树的后序遍历
二叉树的后序列遍历
2.8 二叉树的构建及遍历
二叉树的构建及遍历
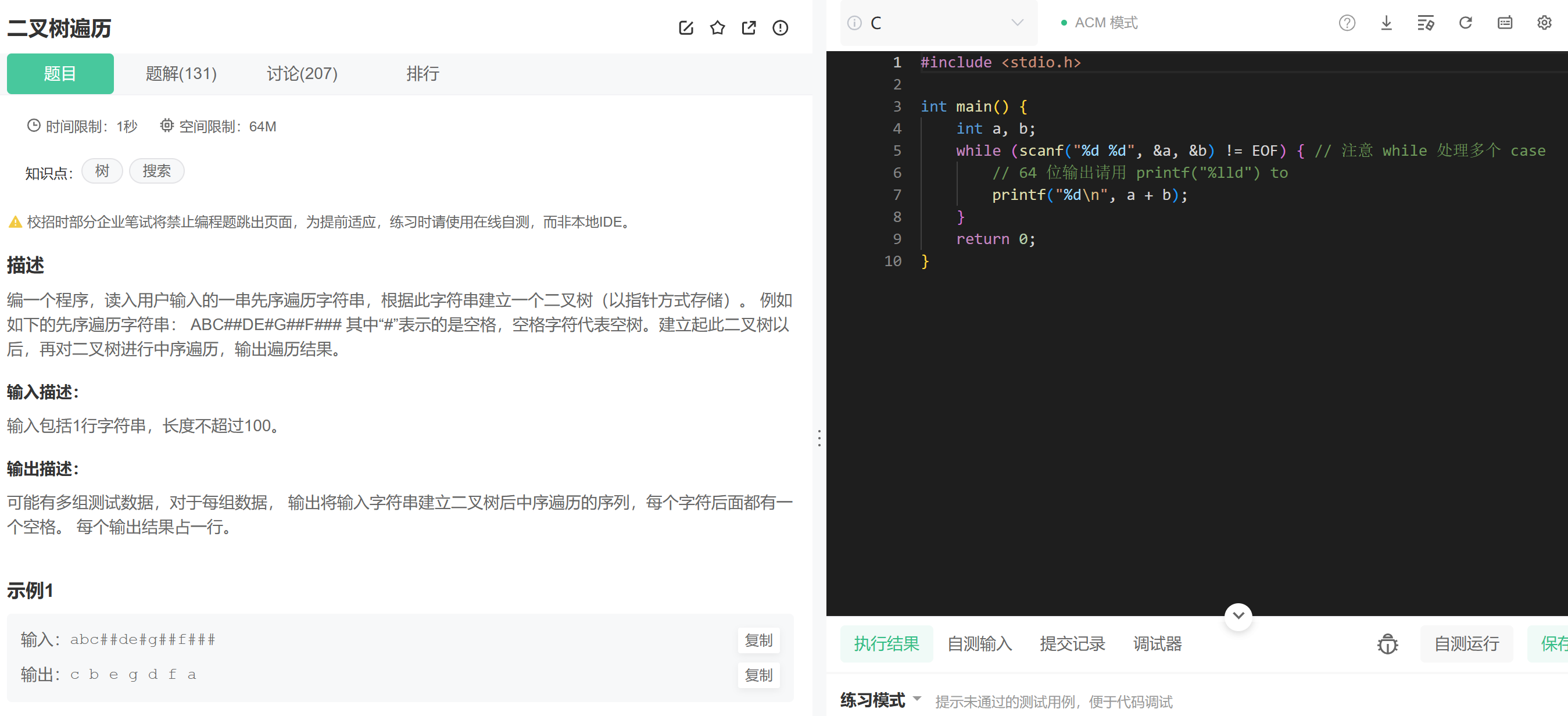

这里只给一种遍历方式字符串是可以画出二叉树的,因为其遍历结果给空树用#标记了,遇到空树就不能继续向下创建节点了
#include <stdio.h>
#include <stdlib.h>
//定义二叉树的结构
typedef struct BinaryTreeNode
{char data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;BTNode* buyNode(char ch)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if(newnode == NULL){perror("malloc fail");exit(1);}newnode->data = ch;newnode->left = newnode->right = NULL;return newnode;
}
//创建二叉树,返回二叉树的根节点
BTNode* createTree(char* arr, int* pi)
{if(arr[(*pi)] == '#'){(*pi)++;return NULL;}//取到的字符不为#,创建二叉树的根节点BTNode* root = buyNode(arr[(*pi)++]);//创建该根节点的左子树和右子树root->left = createTree(arr, pi);root->right = createTree(arr, pi);return root;
}void InOrder(BTNode* root)
{if(root == NULL){return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}int main() {//读取输入的字符串保存在数组中char arr[100];scanf("%s", arr);//根据先序遍历字符串建立二叉树int i = 0;BTNode* root = createTree(arr, &i);//中序遍历InOrder(root);return 0;
}
这里细看一下构建二叉树的逻辑,i从0开始创建A的函数栈帧,取到的* pi不为#,创建根节点A
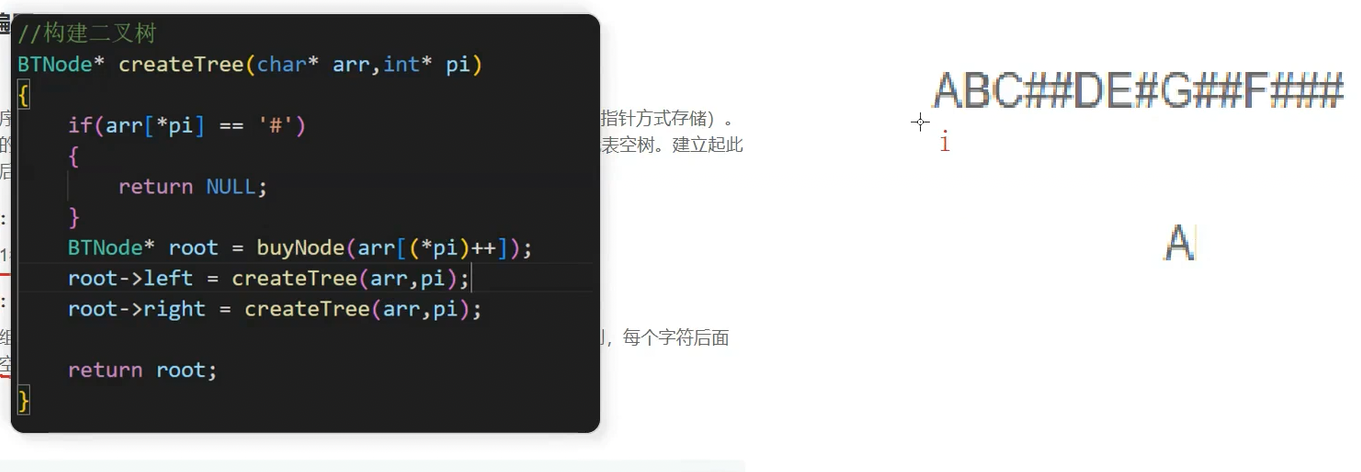
之后i++,创建根节点A的左子树(B),创建B的函数栈帧,在B的函数栈帧中创建根节点B
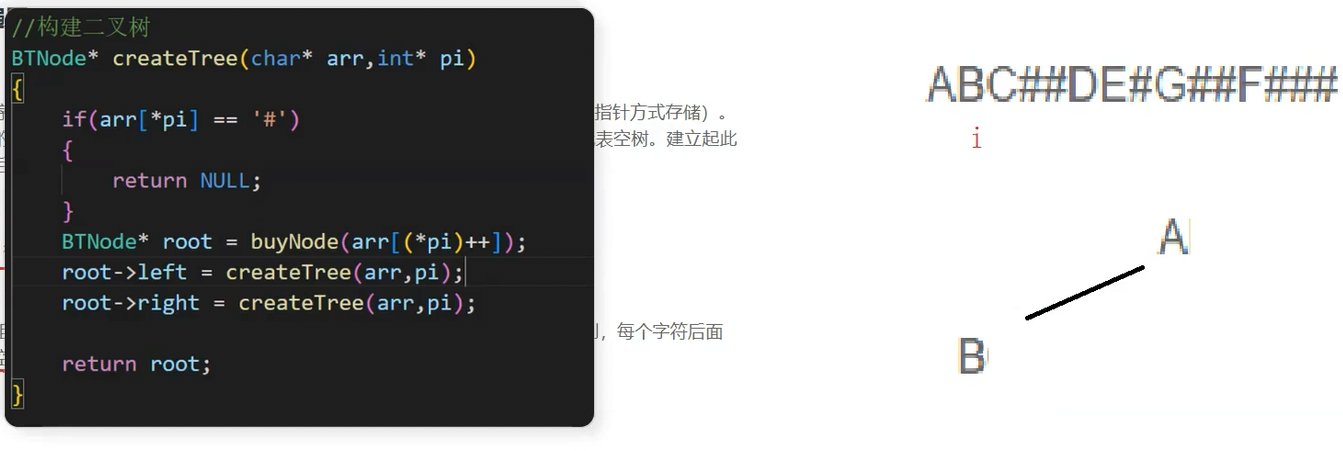
i++,接下来继续创建B的左子树,在C的函数栈帧中创建根节点C
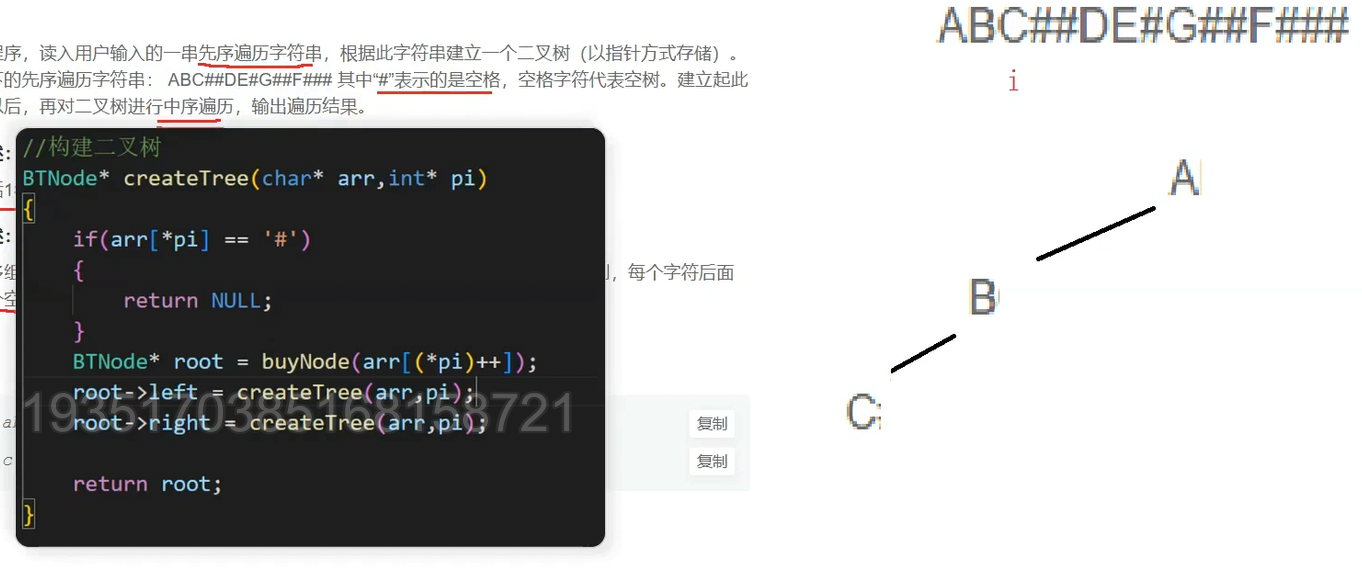
继续创建C的左子树,i++,创建参数为#的函数栈帧,进入栈帧后直接return,回到C的函数栈帧
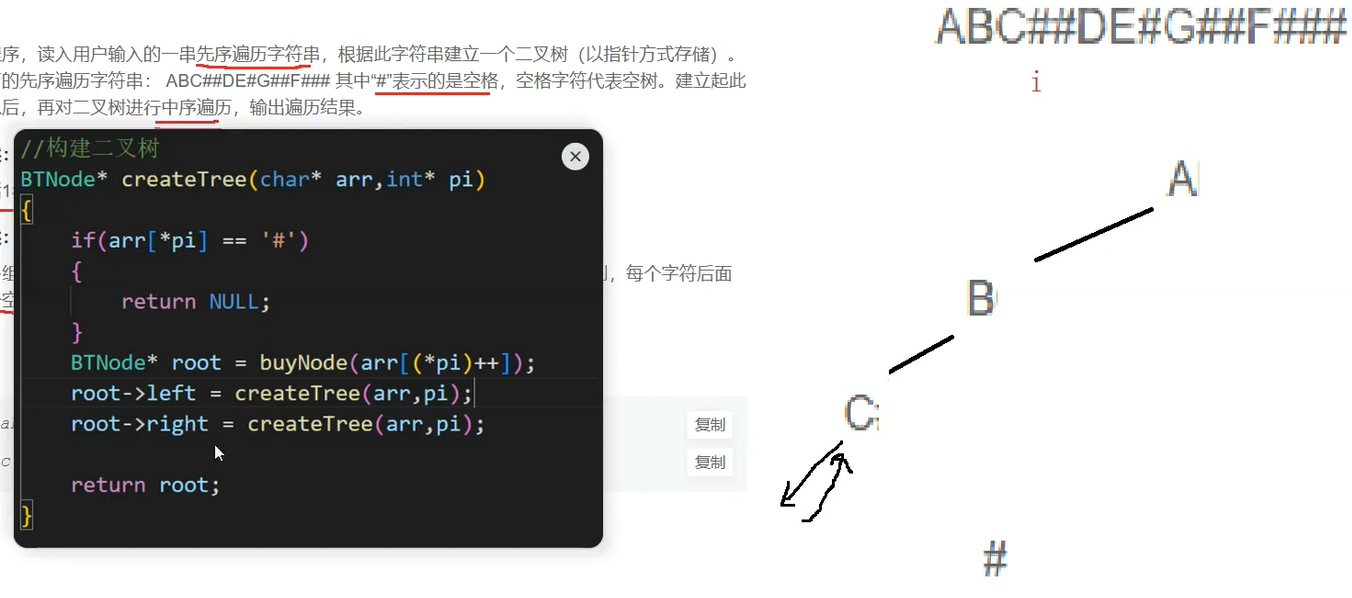
此时C的根节点已经有了,左子树为空,再递归创建C的右子树,但是i此时没有后移了,因判断* pi 等于 #号的时候,i没有继续往下走,所以在if判断中加一句代码
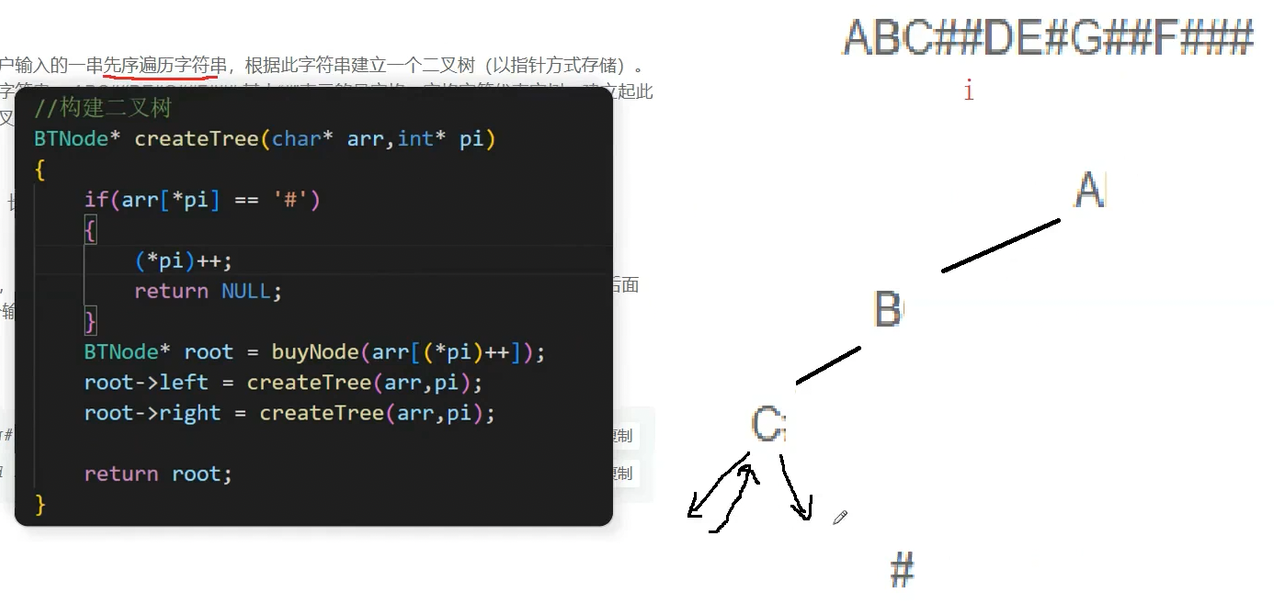
此时创建C的右子树,* pi为#,直接i++,return,回到C的函数栈帧中
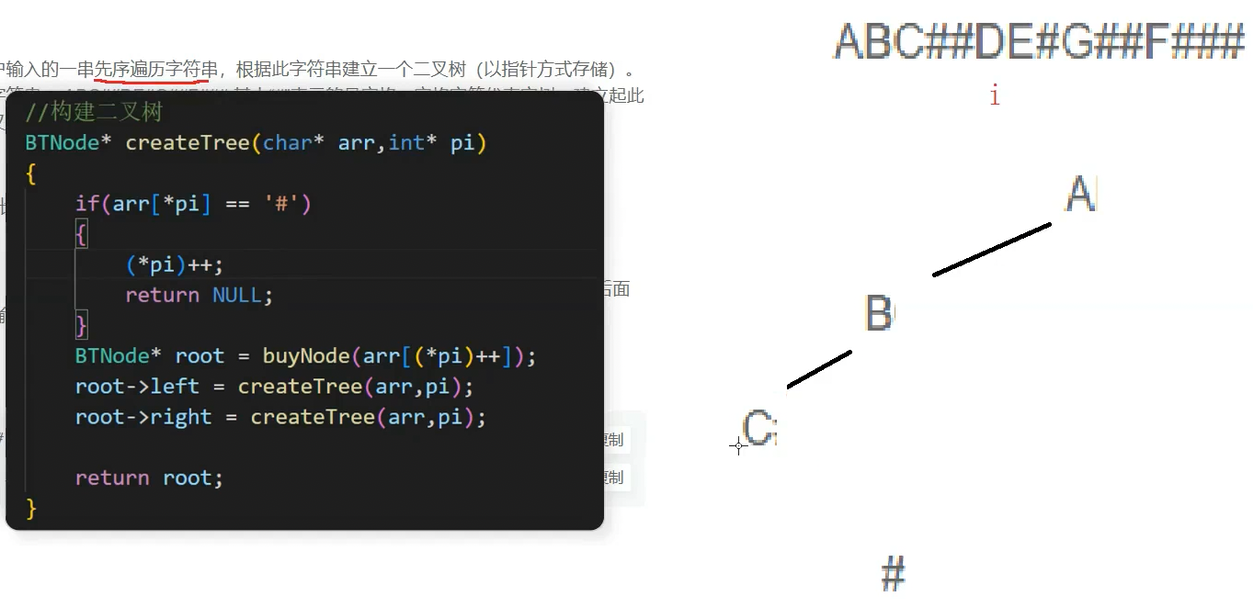
C的左右都为空,直接return root,root就为C,此root是B的左子树,B的左子树创建完成后创建B的右子树(D),D创建完成后i++来到了E

E就是D的左子树,E创建好了之后i继续++,继续创建E的左子树,E的左子树为空,i++来到G后直接返回
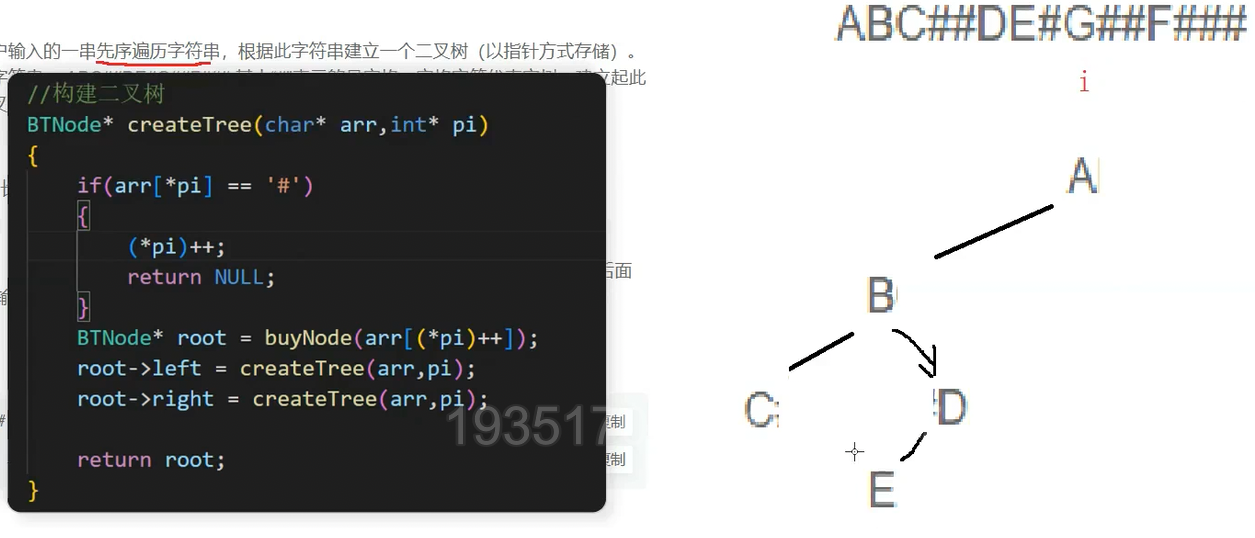
接下来创建E的右子树(G),创建之后i++来到#

G的左右子树都是#,i++两次直接来到F,G的二叉树就构建完成了
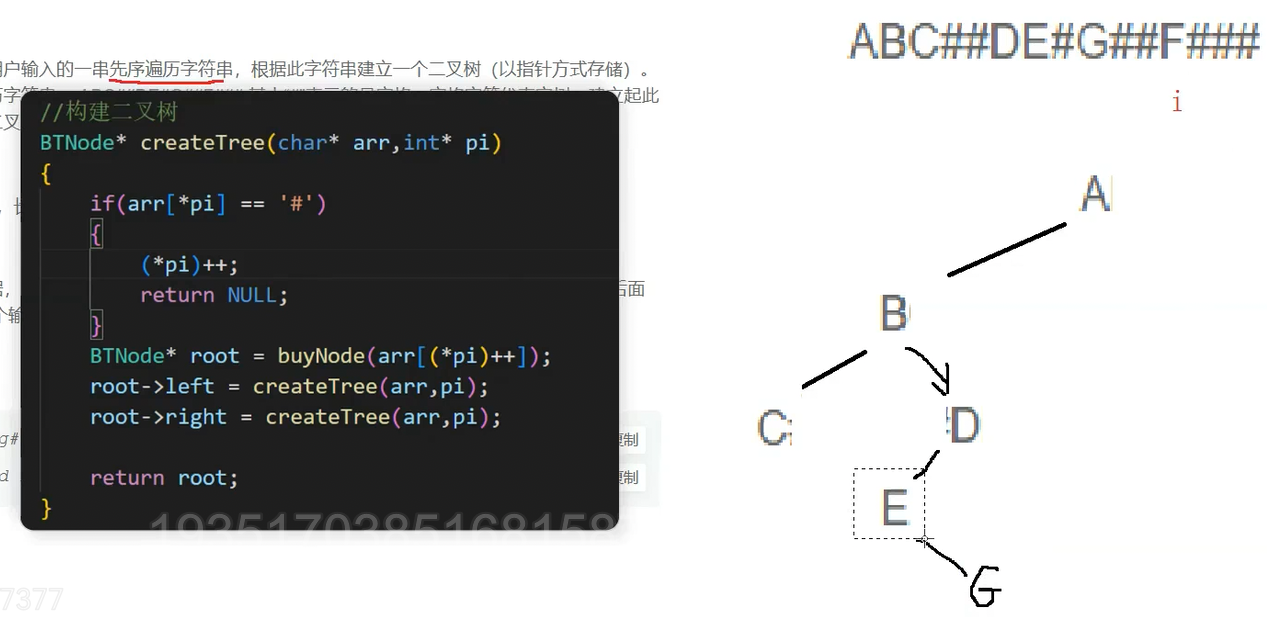
G此时return root来到了E,E的根左右已经构建完了来到D,D的根左已经创建完了,在D的函数栈帧中继续创建D的右子树(F)
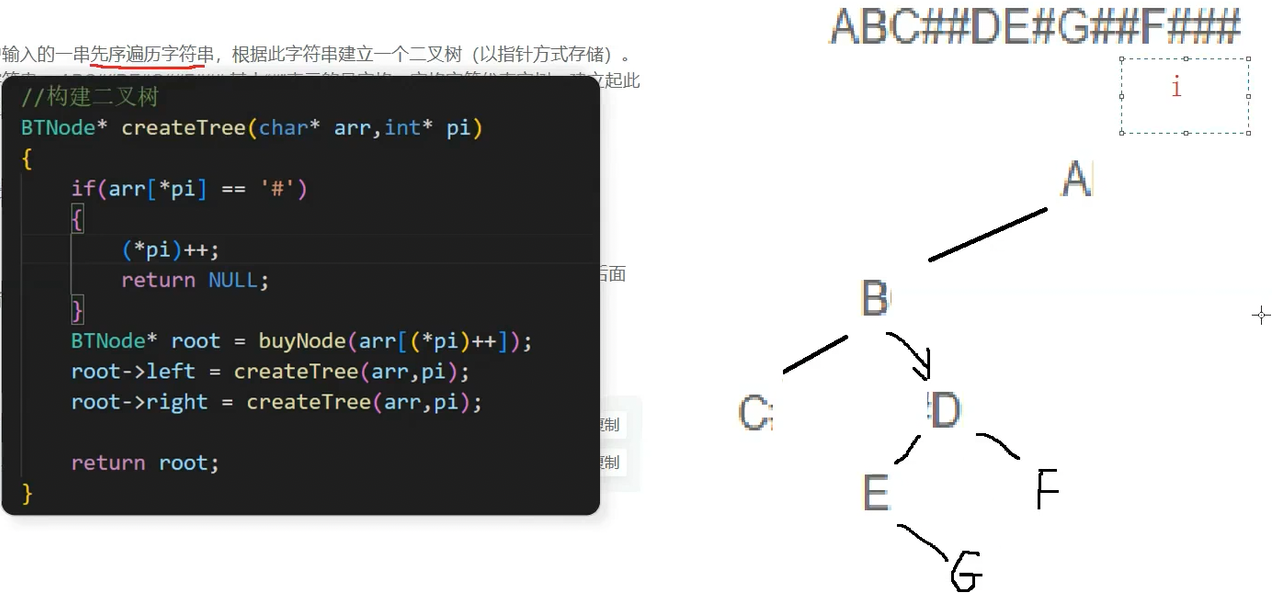
F的根节点创建完成后i++,构建F的左右子树,F的左右子树为#,i++两次

此时F这棵二叉树的左右子树构建完成,在F的函数栈帧中return root,回到D的函数栈帧,D return root回到B,B回到A,A的根左已经构建完了,开始构建A的右子树,A的右子树取到的是#,i直接++,此时二叉树构建完成
结语

