杭州开发网站的公司哪家好wordpress alipay插件

如有问题大概率是我的理解比较片面，欢迎评论区或者私信指正。

总结一下最近的学习情况，情绪在有效学习中起到非常大的作用，外界比较吸引人的东西大多是可以引起自己的某一种情绪共鸣，将自己代入一种预设的情景里然后在自己的脑子里不断演绎而深度思考机制和这个有些类似，但却是强制自己演绎某个问题。前者，更像是顿悟、灵感之类的说法，而后者就有些东施效颦的味道。构建情景，调动自己的某种情绪进而引导自己主动进入演绎过程这种技巧对于研究型的学习和工作而言--如鱼得水。因为这利用了人趋利避害的本能，情绪是这种本能的药引。

一、拓扑排序

一、AOV网络

基本概念

AOV网 是一种用 有向无环图（DAG） 表示工程活动依赖关系的模型。

顶点（Vertex）：代表 活动（Activity）（如“买菜”“切番茄”）。

有向边（Directed Edge）：边 <Vi, Vj> 表示活动 Vi 必须在 Vj 之前完成（Vi 是 Vj 的前驱）。

无环性：图中不能存在循环依赖（否则活动无法执行）。

例如：若 切番茄 → 买菜 且 买菜 → 切番茄，则形成逻辑矛盾。

偏序关系：活动间只有部分存在先后约束（非所有活动都需要严格排序）。

 依赖关系建模

边的方向：弧头活动依赖于弧尾活动。

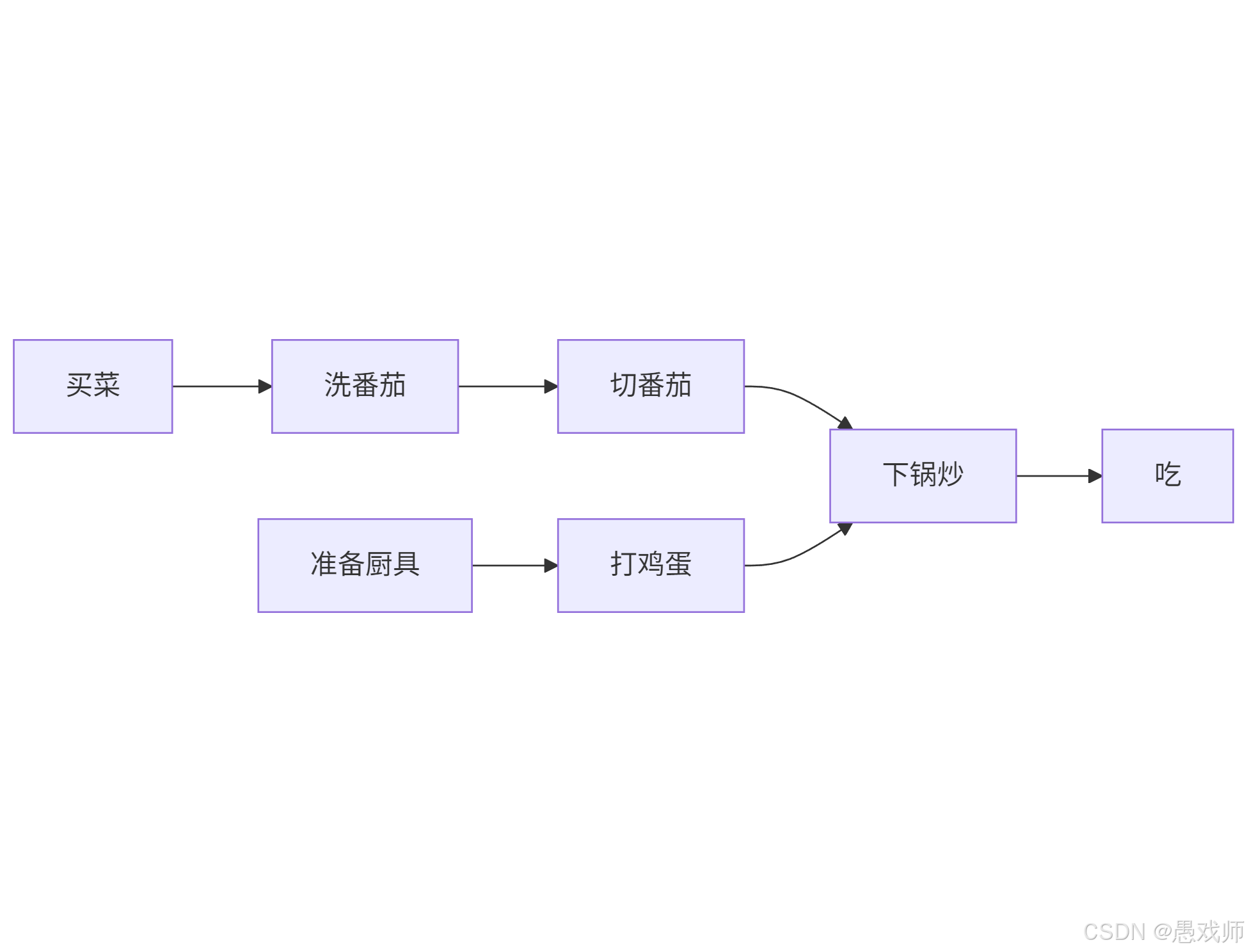
解释：

“下锅炒” 需等待 “切番茄” 和 “打鸡蛋” 完成。

“切番茄” 依赖 “洗番茄”，“洗番茄” 依赖 “买菜”。

2. 拓扑排序的原理

目标：将AOV网中的活动转化为 线性序列，满足所有依赖关系。

规则：若存在路径 A→B，则序列中 A 必须在 B 之前。

示例序列（番茄炒蛋工程）：
准备厨具 → 买菜 → 洗番茄 → 切番茄 → 打鸡蛋 → 下锅炒 → 吃

二、拓扑排序算法

拓扑排序（Topological Sorting） 是一种针对 有向无环图（DAG） 的顶点排序算法。其核心要求是：

若图中存在路径 A→B（即 AA到 B 有依赖关系），则排序结果中 AA必须位于 B 之前。

• 关键特性：

  • 仅适用于 无环有向图（有环图无法拓扑排序）。

  • 结果序列 不唯一（无直接依赖的顶点可任意排序）。

将图的顶点序列化为线性序列 L，满足：

Kahn算法原理

不断移除没有依赖（入度为0）的节点，直到所有节点都被移除，或者发现循环依赖。

找“起点”： 首先，找出图中所有没有任何前置任务（即入度为 0）的节点（任务）。

执行“起点”： 把这些节点拿出来（输出），表示它们可以立即执行。

解除依赖： 移除这些节点发出的所有边（相当于移除它们指向的下游任务的“依赖”）。

更新状态： 由于移除了边，一些下游任务可能就变成了新的“没有前置任务”的节点（即入度减为 0）。

重复过程： 不断重复步骤 1-4，每次都找出并移除当前入度为 0 的节点。

判断结果：

• 如果最终所有节点都被移除了，那么移除节点的顺序就是一个有效的拓扑排序序列（任务执行顺序）。

• 如果最后还剩下节点，但没有任何一个节点的入度为 0，说明图中存在循环依赖（有环），无法进行拓扑排序。

图-拓扑排序_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1XV411X7T7?spm_id_from=333.788.videopod.sections&vd_source=4b89f462036a892baf8931104a1f36b1

Kahn算法代码实现：

import java.util.*;/*** 使用Kahn算法实现拓扑排序的类。* 该类通过维护图的邻接表和各节点的入度，实现对有向无环图（DAG）的拓扑排序。*/
public class KahnTopologicalSort {// 使用邻接表表示有向图private int numVertices;private List<List<Integer>> adjacencyList;private int[] indegree;/*** 构造函数，初始化图的顶点数、邻接表和入度数组。** @param numVertices 图中顶点的数量*/public KahnTopologicalSort(int numVertices) {this.numVertices = numVertices;this.adjacencyList = new ArrayList<>();for (int i = 0; i < numVertices; i++) {adjacencyList.add(new LinkedList<>());}this.indegree = new int[numVertices];}/*** 向图中添加一条有向边。** @param from 起始节点索引* @param to   目标节点索引*/public void addEdge(int from, int to) {adjacencyList.get(from).add(to);indegree[to]++; // 更新目标节点的入度}/*** 使用Kahn算法执行拓扑排序。** @return 拓扑排序后的节点列表* @throws IllegalStateException 如果图中存在环，无法进行拓扑排序时抛出异常*/public List<Integer> topologicalSort() {// 1. 初始化队列（存储入度为0的节点）Queue<Integer> queue = new LinkedList<>();List<Integer> result = new ArrayList<>();// 2. 将所有入度为0的节点加入队列for (int i = 0; i < numVertices; i++) {if (indegree[i] == 0) {queue.add(i);}}// 3. 处理队列中的节点int count = 0; // 记录已处理的节点数量while (!queue.isEmpty()) {int node = queue.poll();result.add(node);count++;// 4. 遍历当前节点的所有邻接节点for (int neighbor : adjacencyList.get(node)) {// 5. 减少邻接节点的入度indegree[neighbor]--;// 6. 如果入度减为0，加入队列if (indegree[neighbor] == 0) {queue.add(neighbor);}}}// 7. 检查是否存在环（关键难点！）if (count != numVertices) {throw new IllegalStateException("图中存在环，无法进行拓扑排序");}return result;}/*** 主方法，用于测试拓扑排序功能。* 示例模拟“番茄炒蛋”工程的依赖关系。** @param args 命令行参数（未使用）*/public static void main(String[] args) {// 创建示例图（番茄炒蛋工程）KahnTopologicalSort graph = new KahnTopologicalSort(7);// 定义节点索引int 准备厨具 = 0, 买菜 = 1, 洗番茄 = 2, 切番茄 = 3,打鸡蛋 = 4, 下锅炒 = 5, 吃 = 6;// 添加边（依赖关系）graph.addEdge(准备厨具, 打鸡蛋);graph.addEdge(准备厨具, 下锅炒);graph.addEdge(买菜, 洗番茄);graph.addEdge(洗番茄, 切番茄);graph.addEdge(切番茄, 下锅炒);graph.addEdge(打鸡蛋, 下锅炒);graph.addEdge(下锅炒, 吃);try {List<Integer> sortedOrder = graph.topologicalSort();System.out.println("拓扑排序结果: ");for (int node : sortedOrder) {switch (node) {case 0:System.out.println("准备厨具");break;case 1:System.out.println("买菜");break;case 2:System.out.println("洗番茄");break;case 3:System.out.println("切番茄");break;case 4:System.out.println("打鸡蛋");break;case 5:System.out.println("下锅炒");break;case 6:System.out.println("吃");break;}}} catch (IllegalStateException e) {System.out.println(e.getMessage());}}
}

Kahn算法练习：

210. 课程表 II - 力扣（LeetCode）https://leetcode.cn/problems/course-schedule-ii/description/

class Solution {public int[] findOrder(int numCourses, int[][] prerequisites) {// 处理边界情况if (numCourses <= 0) {return new int[0];}// 构建图List<List<Integer>> g = new ArrayList<>();for (int i = 0; i < numCourses; i++) {g.add(new LinkedList<>());}int[] inde = new int[numCourses]; // 入度数组// 根据依赖关系构建图for (int[] edg : prerequisites) {int from = edg[1]; // 依赖的来源节点 (必须完成的课程)int to = edg[0];   // 依赖的目标节点 (后续课程)g.get(from).add(to); // 添加边: from → toinde[to]++;         // to节点的入度增加}Deque<Integer> deque = new ArrayDeque<>();// 将所有入度为0的节点加入队列for (int i = 0; i < numCourses; i++) {if (inde[i] == 0) {deque.add(i);}}int[] result = new int[numCourses];int count = 0;while (!deque.isEmpty()) {int node = deque.poll();result[count++] = node;// 遍历当前节点的所有邻接节点for (int nb : g.get(node)) {inde[nb]--;// 如果邻接节点入度降为0，将其加入队列if (inde[nb] == 0) {deque.add(nb);}}}// 检查是否所有节点都被处理 (若存在环则count != numCourses)if (count != numCourses) {return new int[0];}return result;}
}

207. 课程表 - 力扣（LeetCode）https://leetcode.cn/problems/course-schedule/

class Solution {public boolean canFinish(int numCourses, int[][] prerequisites) {//极端if(numCourses<=0)return false;//构建图·邻接表List<List<Integer>> g=new ArrayList<List<Integer>>();//入度数组int[] inde=new int[numCourses];//初始化for(int i=0;i<numCourses;i++){g.add(new LinkedList<>());}for(int[] edg:prerequisites){int from=edg[1];int to=edg[0];g.get(from).add(to);inde[to]++;}//kahnDeque<Integer> deque=new ArrayDeque<>();for(int i=0;i<numCourses;i++){if(inde[i]==0)deque.add(i);}int count=0;while(!deque.isEmpty()){int node =deque.poll();count++;//删除节点及其所有出边->对应邻居节点的入度减一for(int nb:g.get(node)){inde[nb]--;if(inde[nb]==0)deque.add(nb);}}System.out.println(count);return count==numCourses;}
}

三、逆拓扑排序

从后往前排任务，谁没有后续任务谁先出局

逆拓扑排序原理：

1. 找终点：在图中找出一个没有后继任务（即出度为0，没有任何边指向其他任务）的顶点。

2. 输出并删除：输出这个顶点，并把它连同所有指向它的边一起从图中删掉。

3. 重复直到空：不断重复前两步，直到图中没有顶点为止。输出的序列就是逆拓扑排序。

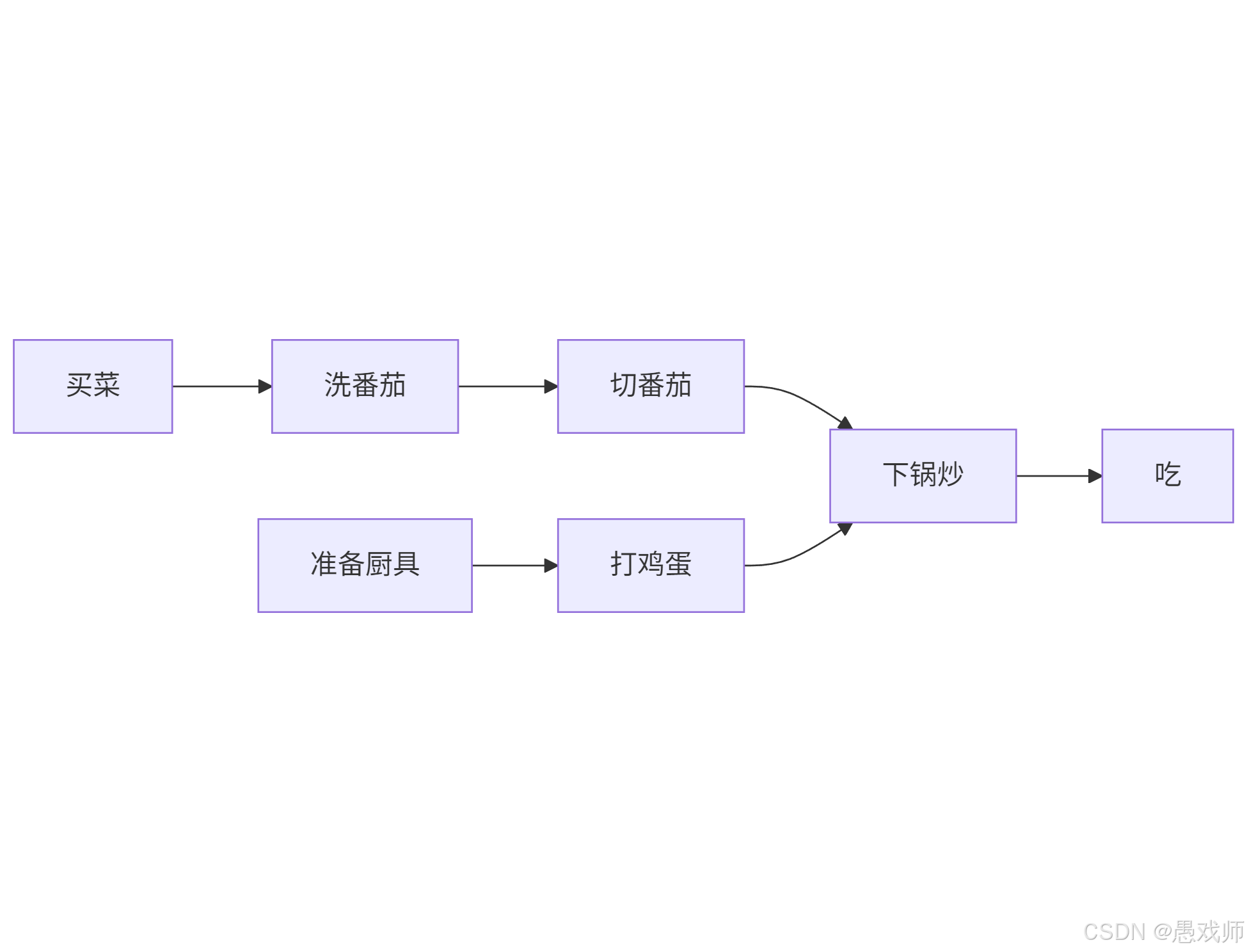
• 拓扑排序（正向）：[准备厨具, 买菜, 洗番茄, 切番茄, 打鸡蛋, 下锅炒, 吃]

• 逆拓扑排序（反向）：[吃, 下锅炒, 切番茄, 洗番茄, 买菜, 打鸡蛋, 准备厨具]

逆拓扑排序代码实现：

import java.util.*;public class InverseTopologicalSort {// 方法1：直接法（基于出度）public static List<Integer> inverseTopoSortDirect(List<Integer>[] graph) {int n = graph.length;// 易错点1：需要逆邻接表（存储每个顶点的前驱）List<Integer>[] inverseGraph = new ArrayList[n];for (int i = 0; i < n; i++) {inverseGraph[i] = new ArrayList<>();}// 难点1：计算每个顶点的出度int[] outDegree = new int[n];for (int u = 0; u < n; u++) {for (int v : graph[u]) {outDegree[u]++;          // 更新u的出度inverseGraph[v].add(u);  // 为v添加前驱u}}Queue<Integer> queue = new LinkedList<>();// 易错点2：初始化队列时需添加所有出度为0的顶点for (int i = 0; i < n; i++) {if (outDegree[i] == 0) {queue.add(i);}}List<Integer> result = new ArrayList<>();while (!queue.isEmpty()) {int v = queue.poll();result.add(v);// 遍历v的所有前驱（指向v的顶点）for (int u : inverseGraph[v]) {outDegree[u]--;  // 难点2：删除边u->v后更新u的出度if (outDegree[u] == 0) {queue.add(u);}}}// 易错点3：检查环if (result.size() != n) {throw new IllegalStateException("图中有环，无法进行逆拓扑排序");}return result;}// 方法2：DFS法（基于回溯时记录顶点）public static List<Integer> inverseTopoSortDFS(List<Integer>[] graph) {int n = graph.length;int[] visited = new int[n]; // 0=未访问, 1=访问中, 2=已访问List<Integer> result = new ArrayList<>();for (int i = 0; i < n; i++) {if (visited[i] == 0) {if (dfs(i, graph, visited, result)) {throw new IllegalStateException("图中有环");}}}// DFS结果是拓扑排序的逆序，直接返回return result;}private static boolean dfs(int u, List<Integer>[] graph, int[] visited, List<Integer> result) {visited[u] = 1; // 标记为访问中for (int v : graph[u]) {if (visited[v] == 0) {if (dfs(v, graph, visited, result)) return true; // 发现环} // 难点3：检测后向边（环）else if (visited[v] == 1) {return true; // 存在环}}visited[u] = 2; // 标记为已访问result.add(u);   // 关键：在递归返回时添加顶点return false;}// 测试用例public static void main(String[] args) {// 构建图（邻接表）int n = 5;List<Integer>[] graph = new ArrayList[n];for (int i = 0; i < n; i++) {graph[i] = new ArrayList<>();}/* 示例图结构：0 -> 21 -> 22 -> 32 -> 4*/graph[0].add(2);graph[1].add(2);graph[2].add(3);graph[2].add(4);// 测试两种方法System.out.println("直接法: " + inverseTopoSortDirect(graph));System.out.println("DFS法:  " + inverseTopoSortDFS(graph));}
}

逆拓扑排序练习

210. 课程表 II - 力扣（LeetCode）https://leetcode.cn/problems/course-schedule-ii/?utm_source=LCUS&utm_medium=ip_redirect&utm_campaign=transfer2china

class Solution {//环判断boolean isCircle=false;//标记数组int[] visited;//结果·模拟栈int[] result;int index;public int[] findOrder(int numCourses, int[][] prerequisites) {// 处理边界情况if (numCourses <= 0) {return new int[0];}visited=new int[numCourses];result=new int[numCourses];index=numCourses-1;//构建图List<List<Integer>> g=new ArrayList<>();for(int i=0;i<numCourses;i++){g.add(new LinkedList<Integer>());}for(int[] e: prerequisites){int from=e[1],to=e[0];g.get(from).add(to);}//对每个未搜索过的点开始深度优先搜索for(int i=0;i<numCourses;i++){if(visited[i]==0){dfs(i,g);}}if(isCircle)return new int[0];return result;}public void dfs(int u,List<List<Integer>> g){visited[u]=1;for(int v : g.get(u)){if(visited[v]==0){dfs(v,g);if(isCircle)return ;}else if(visited[v]==1){//自己邻居也在访问必定有环isCircle=true;return;}}visited[u]=2;result[index--]=u;}}

二、关键路径

一、AOE网（Activity On Edge Network）

基本概念

AOE网是一种带权有向图，用于描述工程项目的流程依赖关系。

顶点（事件）：表示项目中某个里程碑状态（如“工程开始”“材料准备完成”）。

有向边（活动）：表示具体任务（如“采购材料”“组装部件”）。

边权值：表示完成活动所需的时间或资源开销。

核心特征

唯一源点：入度为 0 的顶点，代表工程起点（如“项目启动”）。

唯一汇点：出度为 0 的顶点，代表工程终点（如“项目交付”）。

活动依赖：事件发生后，其出发的活动才能开始。

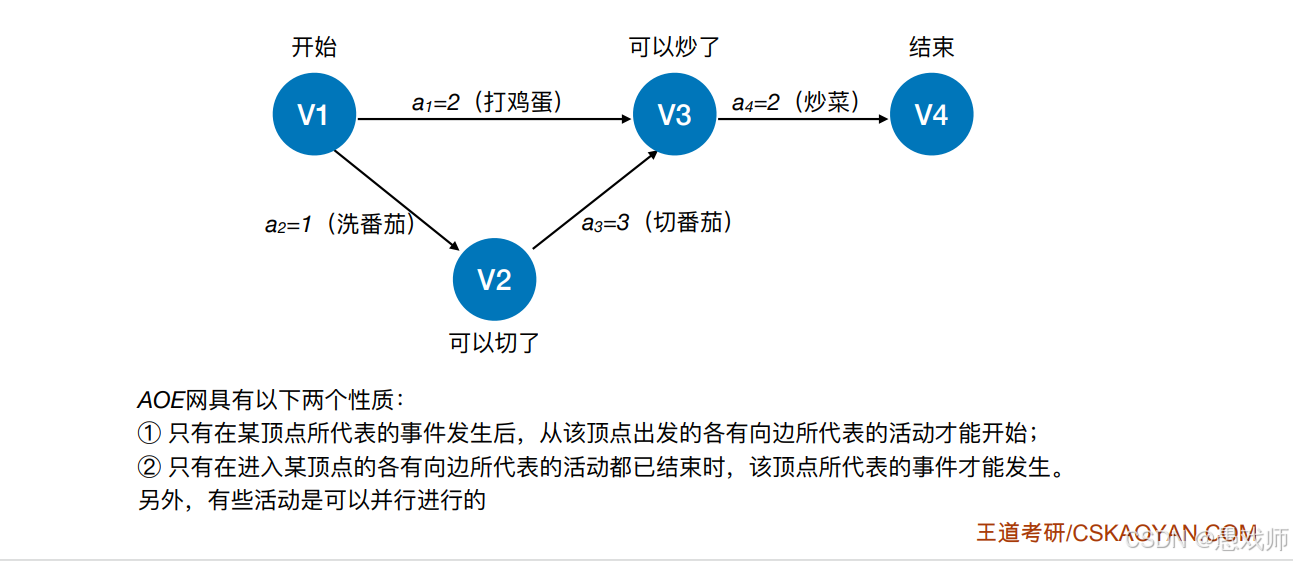
事件触发的约束条件

• 事件发生前提：进入该事件的所有活动必须已完成。

  例如：事件 V3（可以炒菜） 发生需满足：

  • 活动 a₁（打鸡蛋） 完成

  • 活动 a₃（切番茄） 完成

• 活动启动条件：只有事件的前驱活动完成后，其后继活动才能开始。

并行性

• 非依赖的活动可并行执行（如 打鸡蛋 和 洗番茄 可同时进行）。

关键路径原理

• 关键路径：从源点到汇点的最长路径（总耗时最大），决定工程最短工期。

• 关键活动：关键路径上的活动，其延迟将导致整个工程延期。

AOE网 vs. AOV网

特性	AOE网	AOV网
元素含义	边表示活动，顶点表示事件	顶点表示活动，边表示顺序
权值	边有权值（活动耗时）	边无权值
核心功能	计算关键路径与最短工期	拓扑排序确定任务执行顺序
应用场景	项目管理、工期优化	任务调度、依赖关系分析

二、关键路径求解

手算法：

6.4.5_关键路径_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1b7411N798?spm_id_from=333.788.videopod.sections&vd_source=4b89f462036a892baf8931104a1f36b1&p=71

步骤1：确定拓扑序

步骤2：求事件最早发生时间

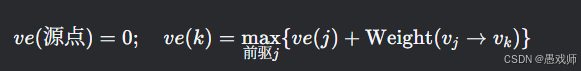
步骤3：求事件最晚发生时间

步骤4：求活动最早发生时间

步骤5：求活动最晚发生时间

步骤6：求活动的时间余量

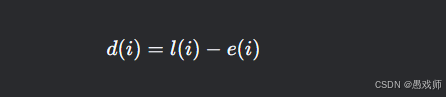
步骤7：活动时间余量为0的活动为关键活动，路径为关键路径

代码实现：

import java.util.*;public class CriticalPath {static class Edge {int from;int to;int weight;String name;public Edge(int from, int to, int weight, String name) {this.from = from;this.to = to;this.weight = weight;this.name = name;}}public static List<String> findCriticalPath(List<List<Edge>> graph) {int n = graph.size();// 1. 计算入度和出度int[] inDegree = new int[n];int[] outDegree = new int[n];for (int i = 0; i < n; i++) {for (Edge edge : graph.get(i)) {inDegree[edge.to]++;outDegree[edge.from]++;}}// 2. 找到源点和汇点int source = -1, sink = -1;for (int i = 0; i < n; i++) {if (inDegree[i] == 0) source = i;if (outDegree[i] == 0) sink = i;}if (source == -1 || sink == -1) {throw new IllegalArgumentException("Invalid AOE network");}// 3. 拓扑排序并计算 veint[] ve = new int[n];Arrays.fill(ve, 0);Queue<Integer> queue = new LinkedList<>();queue.offer(source);List<Integer> topoOrder = new ArrayList<>();int[] tempInDegree = inDegree.clone();while (!queue.isEmpty()) {int u = queue.poll();topoOrder.add(u);for (Edge edge : graph.get(u)) {int v = edge.to;ve[v] = Math.max(ve[v], ve[u] + edge.weight);if (--tempInDegree[v] == 0) {queue.offer(v);}}}// 4. 逆拓扑排序计算 vlint[] vl = new int[n];Arrays.fill(vl, Integer.MAX_VALUE);vl[sink] = ve[sink];Collections.reverse(topoOrder);for (int u : topoOrder) {for (Edge edge : graph.get(u)) {int v = edge.to;if (vl[u] > vl[v] - edge.weight) {vl[u] = vl[v] - edge.weight;}}}// 5. 计算活动的 e, l, dMap<String, Integer> eMap = new HashMap<>();Map<String, Integer> lMap = new HashMap<>();Map<String, Integer> dMap = new HashMap<>();List<String> criticalActivities = new ArrayList<>();for (int u = 0; u < n; u++) {for (Edge edge : graph.get(u)) {// e(i) = ve[u]int e = ve[u];// l(i) = vl[v] - weightint l = vl[edge.to] - edge.weight;int d = l - e;eMap.put(edge.name, e);lMap.put(edge.name, l);dMap.put(edge.name, d);if (d == 0) {criticalActivities.add(edge.name);}}}// 6. 构建关键路径return criticalActivities;}public static void main(String[] args) {// 构建示例图 (Page 14)int n = 6; // 6个顶点List<List<Edge>> graph = new ArrayList<>();for (int i = 0; i < n; i++) {graph.add(new ArrayList<>());}// 添加边 (活动)graph.get(0).add(new Edge(0, 1, 3, "a1")); // V1->V2graph.get(0).add(new Edge(0, 2, 2, "a2")); // V1->V3graph.get(1).add(new Edge(1, 3, 2, "a3")); // V2->V4graph.get(1).add(new Edge(1, 4, 4, "a5")); // V2->V5graph.get(2).add(new Edge(2, 3, 3, "a4")); // V3->V4graph.get(3).add(new Edge(3, 5, 2, "a7")); // V4->V6graph.get(4).add(new Edge(4, 5, 1, "a8")); // V5->V6List<String> criticalPath = findCriticalPath(graph);System.out.println("关键活动: " + criticalPath);System.out.println("关键路径: V1 -> V3 -> V4 -> V6");}
}