二叉搜索树学习笔记

二叉搜索树学习笔记

简介

二叉搜索树（Binary Search Tree, BST）是一种有根的二叉树，每个节点有权值。满足其中序遍历为有序序列（空串也是有序的）。

或者这样定义：

1. 空树是二叉搜索树。
2. 对于一个节点 $a$，$a$ 的左子树和右子树都是二叉搜索树，并且满足：
   1. $a$ 的左子树中所有节点的权值都小于 $a$。
   2. $a$ 的右子树中所有节点的权值都大于 $a$。

利用二叉搜索树，我们可以实现一个“集合”类型（如 C++ STL 中 std::set）。若要支持可重集（如 C++ STL 中 set::multiset），可以再多一个卫星数据——出现次数。

为了方便，我们这里令一个节点 $k$ 的权值、左子结点、右子节点分别为 $k_v,k_l$ 和 $k_r$。令以一个节点 $k$ 为根的子树为 $T(k)$，而一棵树 $T$ 的大小记为 $s(T)$。

操作

注意，有些操作如果操作前/操作后 BST 为空，则可能需要特殊处理。很简单这里不讲了。

建树

什么都不需要干。

辅助操作：旋转

旋转（rotate），是一个很有用的操作，分为左旋和右旋。

通俗来讲，对于一个节点进行左旋（left rotate），实际上就是把它的右子节点“提到上面来”。实际上有略微的不同（提完之前的那个右子节点的左子树会变成根节点的右子树，这个过程还是挺形象的）。右旋（right rotate）类似，可以参考下图和下下图。

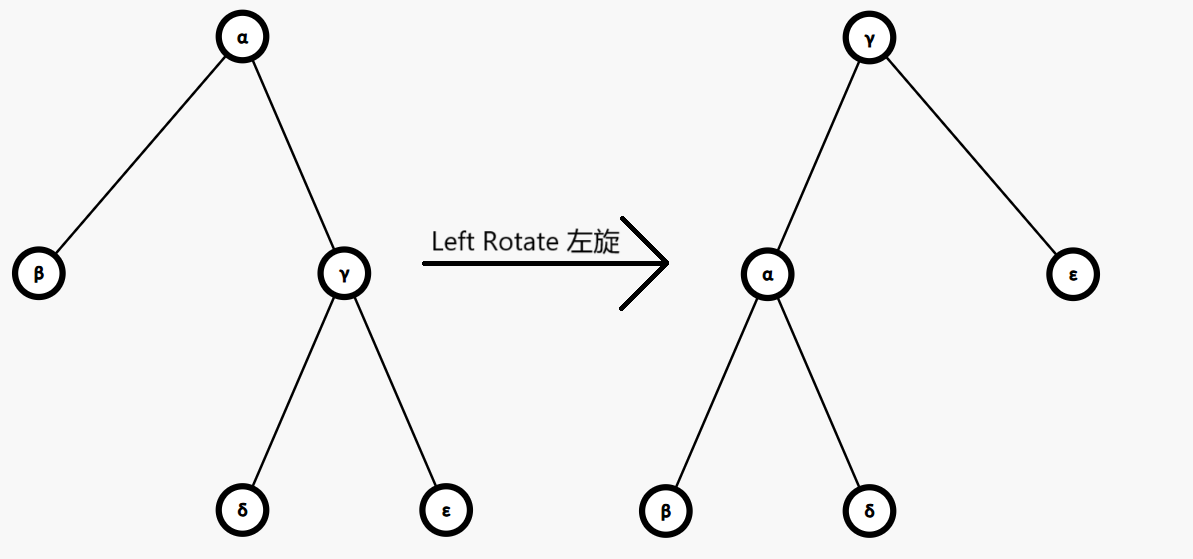
为什么旋转很有用？旋转并不会违反二叉搜索树性质。这样，我们就可以在维持二叉搜索树性质的同时，改变二叉搜索树的形态。

旋转需要的条件：需要父节点和某一个子节点（左旋就是右子节点，因为旋转之后变成了新的父节点和新的左子结点。右旋就是左子结点）。如果不存在其它节点，则当做空处理。

一般来讲，两个描述“针对子节点进行旋转操作”和“针对父节点进行左旋/右旋操作”中前者要好（含义上是等价的），因为针对子节点只能有最多一种旋转操作（没有可用旋转当且仅当是根节点），而针对父节点则最多有两种。

插入元素

显然，在二叉搜索树中可以这样插入元素：

1. 设定“当前节点 $g$”为根节点，要插入的元素权值为 $k$。
2. 进行分类讨论：
   1. 如果 $k=v(g)$，则说明元素已经存在，依据情况执行操作然后结束（如可重集则将卫星数据出现次数增加 $1$）。
   2. 如果 $k<v(g)$，则说明 $k$ 应当插入在 $g$ 左子树中，若 $g_l$ 存在则执行 $g\leftarrow g_l$ 然后回到第二步，否则插入到 $g_l$ 的位置并结束。
   3. 如果 $k>v(g)$，则类似上面执行操作。

搜索元素

类似上面的“插入元素”，只不过在 $k=v(g)$ 时说明找到了元素，$k\ne v(g)$ 时如果对应左/右子结点不存在则说明没找到，并且不会插入元素。

查询最大/最小元素

只需要一直往左子结点走（查询最小）直到没有左子结点，或者一直往右子节点走（查询最大）直到没有右子节点即可。

同样，我们可以查询以某个节点为根节点的最大/最小值。

注意当一直往左（右）的时候走到一个只有右（左）子节点的节点的时候不能往右（左）走，因为那样会更大（小）。

删除元素

首先使用“搜索元素”找到对应元素 $g$（假设存在）。

然后看情况可能需要执行操作，也可能执行完退出（如，可重集对应出现次数 $>1$ 时，只需要把出现次数 $-1$ 并退出即可）。

如果没有退出，就有两种删除方法：

第一种：把 $g$ 旋转到叶子结点（具体来讲，每次选择一个可用子节点进行旋转，每次深度会增加 $1$），然后直接删除即可。

第二种：如果 $g$ 是叶子结点则直接删除。否则如果 $g$ 有一个子节点，那么那 $g$ 的子树替代自身即可（正确性自证不难），如果有两个则用其左子树中的最大节点或其右子树中的最小节点代替之即可。注意“代替”是指先用自己的信息覆盖 $g$，然后删除自身。这里删除也需要递归地用这种方法删除。

查询元素排名

根据元素查询排名。

排名指的是第几小，下同。第几大也很简单。

要支持这个，需要在维护上述信息的同时维护子树大小（下同，如果提到了子树大小）。维护方法也很简单就不多说了。需要注意的是，如果维护的是可重集（并且使用附加数据域“出现次数”实现），统计子树大小的时候需要统计出现次数之和。

这个非常好想，在搜索元素的过程中，如果是走到右子树就把排名（初始为 $0$）加上 $s(T(g_l))+1$（$s(T(g_l))+1$ 就是 $g$ 的左子树大小），否则不变，找到的时候加上 $1$（或者直接初始化为 $1$）。

查询排名元素

根据排名查询元素。

“查询元素排名”的逆操作。我们只需要在搜索元素的过程中，如果排名 $=s(T(g_l))+1$（$s(T(g_l))$ 就是 $g$ 的左子树大小），则就是 $g$。如果小于，则往左子树搜索，排名不变。如果大于，则往右子树搜索，并且排名减少 $s(T(g_l))+1$。

如果是拓展的排名（即元素可能不存在，定义为比它小的元素个数 $+1$）则也相似，不多讲。

查询前驱/后继节点

查询一个值的前驱节点。也就是，最大的比它小的节点。后继类似，以前驱为例。

我们需要在满足小于某个数 $k$ 的所有节点中查询最大值。

那么从根节点开始，每次如果发现当前节点 $v(g)=k$ 则查询左子树的 $\max$，如果 $v(g)<k$ 则往左子树走（因为右子树中全都比它大），如果 $v(g)>k$，则如果右子树中存在前驱结点则直接返回右子树的前驱，否则返回 $g$。

可以使用递归实现，也可以记录一个 $\max$。我是用的是前者。

时间复杂度

正确性证明很显然，这里略去。

好了现在有不显然的一点了，关于查询前驱/后继的正确性证明？

容易发现，设 $h$ 为 BST 高度，则除去建树和旋转（这俩是 $\Theta (1)$ 的），所有操作的时间复杂度都是 $\mathcal{O}(h)$ 的（严格来讲加上建树也可以，但是有点魔怔）。

补充证明：为什么删除元素时间复杂度也是 $\mathcal{O}(h)$？

第一种方法：因为每次旋转之后要删除的元素都会下沉 $1$ 个节点（深度增加 $1$），最多会进行 $h-1$ 次旋转，每次旋转是 $\Theta (1)$ 的。

第二种方法：每次深度最少 $+1$，并且每次查找最大/最小值花费的时间与深度的增量成正比。

所以说二叉搜索树的“平衡性”是一个问题，如果二叉树非常“瘦长”（比如极端情况退化成链），则时间复杂度也会退化（如链就是 $\mathcal{O}(n)$，相当于朴素算法，常数还更大）。

这个时候就需要引进各种平衡方法了，加上平衡方法的 BST 称为平衡树。

平衡树

• Treap 学习笔记。
• AVL 树学习笔记。
• etc。

代码实现

这是使用旋转实现删除的方法。这个代码能够在洛谷 P3369 【模版】普通平衡树 中获得 $91$ 分的好成绩。最后一个点卡普通 BST。

#include <cstdio>
#include <cstdlib>using namespace std;class bst_node
{
public:int num, cnt, sz;bst_node* fa, * l, * r;void calcsz(){sz = cnt;if (l) sz += l->sz;if (r) sz += r->sz;}bool checksz() { return cnt >= 1 && sz == cnt + (l ? l->sz : 0) + (r ? r->sz : 0); }// 旋转。效果：维持二叉搜索树性质。同时把自己的节点高度提升 1，父节点高度降低 1。bool rotate(){if (!fa) return false; // 是根节点，旋转个毛（├┼┼┘：？我：？？？）if (this == fa->l){// 进行右旋。// 思考：什么指针不变？// 答案：自己的左子树不变，父节点的右子树不变。// 什么东西变了？// 自己的右子节点变成了父节点，父节点的父节点变成了自己。// 同时父节点的左子结点变成了自己的右子树。auto f = fa, ff = f->fa;fa->l = r; if (r) r->fa = fa;r = fa; fa->fa = this;fa = ff;if (ff){if (ff->r == f) ff->r = this;else ff->l = this;}}else{// 同理。auto f = fa, ff = f->fa;fa->r = l; if (l) l->fa = fa;l = fa; fa->fa = this;fa = ff;if (ff){if (ff->r == f) ff->r = this;else ff->l = this;}}// 最后维护一下 sz。cnt 和 num 是节点自己的数据，不需要变化。if (l) l->calcsz();if (r) r->calcsz();calcsz();return true;}// 对左子结点旋转。自身高度降低 1。bool rotate_l() { if (!l) return false; return l->rotate(); }// 对右子节点旋转。自身高度降低 1。bool rotate_r() { if (!r) return false; return r->rotate(); }// 自身高度降低 1。bool dec_height() { return rotate_l() || rotate_r(); }
};class bst
{bst_node* rt = nullptr;
public:bst() {}bst_node* search(int x){// Search x in the BSTbst_node* k = rt;while (k){if (x == k->num) return k;else if (x < k->num) k = k->l;else k = k->r;}return nullptr; // Not found}bst_node* qmax(bst_node* rt){while (rt){if (rt->r) rt = rt->r;else return rt;}return rt;}bst_node* qmax() { return qmax(rt); }bst_node* qmin(bst_node* rt){while (rt){if (rt->l) rt = rt->l;else return rt;}return rt;}bst_node* qmin() { return qmin(rt); }bst_node* prev(int x, bst_node* k){if (k == nullptr) return nullptr;if (x == k->num) return qmax(k->l);else if (x < k->num) return prev(x, k->l);else{bst_node* res = prev(x, k->r);return res ? res : k;}}bst_node* prev(int x) { return prev(x, rt); }bst_node* next(int x, bst_node* k){if (k == nullptr) return nullptr;if (x == k->num) return qmin(k->r);else if (x > k->num) return next(x, k->r);else{bst_node* res = next(x, k->l);return res ? res : k;}}bst_node* next(int x) { return next(x, rt); }bst_node* insert(int x){if (rt == nullptr) return rt = new bst_node{ x, 1, 1, nullptr, nullptr, nullptr };bst_node* k = rt;while (k){if (x == k->num){k->cnt++;auto res = k;while (k){k->sz++;k = k->fa;}return res;}else if (x < k->num){if (k->l) k = k->l;else{bst_node* res;k->l = res = new bst_node{ x, 1, 1, k, nullptr, nullptr };while (k){k->sz++;k = k->fa;}return res;}}else{if (k->r) k = k->r;else{bst_node* res;k->r = res = new bst_node{ x, 1, 1, k, nullptr, nullptr };while (k){k->sz++;k = k->fa;}return res;}}}}void remove_one(bst_node* x){if (x->cnt > 1){x->cnt--;while (x){x->sz--;x = x->fa;}return;}if (x->l == nullptr && x->r == nullptr){if (rt == x){rt = nullptr;delete x;}else{auto y = x->fa;if (x == y->l) y->l = nullptr;else y->r = nullptr;delete x;x = y;while (x){x->sz--;x = x->fa;}}return;}while (x->dec_height()); // 哇这么好写if (x == x->fa->l) x->fa->l = nullptr;else x->fa->r = nullptr;while (x){x->sz--;x = x->fa;}delete x;while (rt->fa) rt = rt->fa;}void remove_one(int x) { remove_one(search(x)); }int getrank(int x){int rk = 1;bst_node* g = rt;while (g){if (x < g->num) g = g->l;else if (x == g->num) return rk + (g->l ? g->l->sz : 0);else{rk += g->cnt + (g->l ? g->l->sz : 0);g = g->r;}}return rk;}bst_node* kth(int rk){bst_node* g = rt;while (g){if (!g->l && !g->r) return g;else if (rk >= (g->l ? g->l->sz : 0) + 1 && rk <= (g->l ? g->l->sz : 0) + g->cnt) return g;else if (g->l && !g->r) g = g->l;else if (!g->l && g->r){rk -= g->cnt;g = g->r;}else if (rk <= g->l->sz) g = g->l;else{rk -= g->l->sz + g->cnt;g = g->r;}}return g;}// 还算有用的两个函数，可以看看你有没有写挂。// cheque 和 check 谐音。bool cheque(bst_node* rt){if (!rt->checksz()) return false;if (rt->l && (rt->l->fa != rt || rt->l->num >= rt->num)) return false;if (rt->r && (rt->r->fa != rt || rt->r->num <= rt->num)) return false;if (rt->l && !cheque(rt->l)) return false;if (rt->r && !cheque(rt->r)) return false;return true;}bool check() { return rt->fa == nullptr && cheque(rt); }
};int main()
{int n;scanf("%d", &n);bst k;int cnt = 0;for (int i = 1; i <= n; i++){int opt, x;scanf("%d%d", &opt, &x);switch (opt){case 1: k.insert(x); break;case 2: k.remove_one(x); break;case 3: printf("%d\n", k.getrank(x)); cnt++; break;case 4: printf("%d\n", k.kth(x)->num); cnt++; break;case 5: printf("%d\n", k.prev(x)->num); cnt++; break;case 6: printf("%d\n", k.next(x)->num); cnt++; break;}}return 0;
}

如果是递归删除，则首先增加一个 remove_all 函数：

void remove_all(bst_node* x)
{if (x->l == nullptr && x->r == nullptr){if (rt == x){rt = nullptr;delete x;}else{auto y = x->fa;if (x == y->l) y->l = nullptr;else y->r = nullptr;delete x;x = y;while (x){x->calcsz();x = x->fa;}}return;}if (x->l == nullptr || x->r == nullptr){if (x->fa){if (x->l != nullptr){if (x->fa->l == x) x->fa->l = x->l;else x->fa->r = x->l;x->l->fa = x->fa;}else{if (x->fa->l == x) x->fa->l = x->r;else x->fa->r = x->r;x->r->fa = x->fa;}}else{if (x->l){rt = x->l;x->l->fa = nullptr;}else{rt = x->r;x->r->fa = nullptr;}}while (x){x->calcsz();x = x->fa;}delete x;return;}bst_node* k = qmax(x->l);x->num = k->num;x->cnt = k->cnt;remove_all(k);
}

然后需要把 remove_one(bst_node *) 代码改为：

void remove_one(bst_node* x)
{if (x->cnt > 1){x->cnt--;while (x){x->calcsz();x = x->fa;}return;}remove_all(x);
}

可以获得同样的分数。

彩蛋

AI 都会旋转和字符画，你不可能还不会吧：