【算法】day15 动态规划

1、最大子数组和 hot

题目：53. 最大子数组和 - 力扣（LeetCode）

分析：

• 状态表示：在所有以 i 位置为结尾的连续子数组中找到和最大的子数组，最大和为 dp[i]。

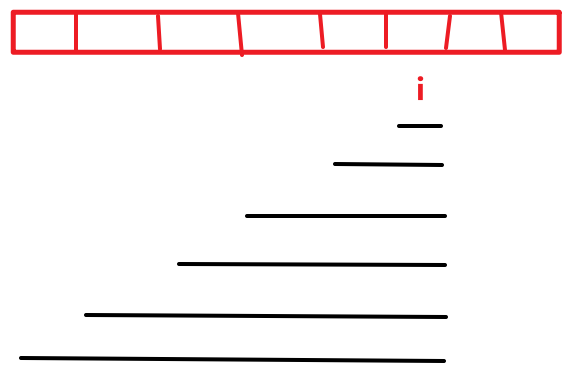
• 状态转移方程：dp[i] = max(nums[i], dp[i-1]+nums[i])，即第一种情况和下面的所有子数组中的最大和比较，哪个最大。
• 初始值：以 0 结尾的最大和 dp[0] = nums[0] = 0。不能使用上面的公式，dp 下标会越界。
• 获取结果的流程：i 从 1 开始遍历，生成 dp 数组，同时获取 dp 中的最大值（以 0~n-1 结尾的连续子数组中的最大和）。

代码：

class Solution {public int maxSubArray(int[] nums) {int[] dp = new int[nums.length];dp[0] = nums[0];int max = dp[0];for (int i = 1; i < nums.length; i++) {dp[i] = Math.max(nums[i], dp[i-1]+nums[i]);if (dp[i] > max) max = dp[i];}return max;}
}

2、单词拆分 hot

题目：139. 单词拆分 - 力扣（LeetCode）

分析：

• 状态表示：以 i 结尾的子字符串是否能由字典中的字符串组成。
• 状态转移方程：dp[i] = dp[j-1] && s(j, i)，即 以 j-1 为结尾的子字符串能由字典中的字符串组成，且字符串 s(j, i) 在字典中。(0 <= j <= i)

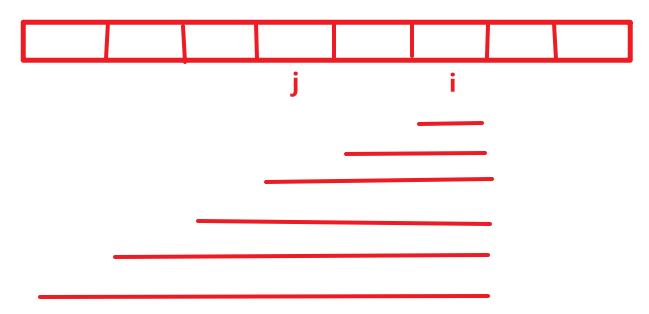
• 边界考虑：j 不能从 0 开始遍历，因为 j-1 会越界。j=0 时，dp[j-1] 代表着空字符串能不能由字典里的字符串组成，肯定为 true。我们直接让 j = 0 时，dp[j-1] 代表着 true。
• 获取结果的流程：i 从 0 开始遍历，j 遍历 以 i 结尾的各种字符串 s(j, i)，更新 dp[i]。因为我们只需要判断存不存在，所以找到一个 dp[i]=true 就退出内循环，计算下一个 dp[i]（不然后面为 false 的结果会把前面为 true 的覆盖，导致错误判断为 dp[i] = false）。最终我们返回 dp[n-1] 的结果即可。

代码：

class Solution {public boolean wordBreak(String s, List<String> wordDict) {int n = s.length();boolean[] dp = new boolean[n];// 构造哈希表，每次从哈希表查 s(j,i) 是否是字典里的单词Set<String> set = new HashSet<>();for (String word : wordDict) set.add(word);for (int i = 0; i < n; i++) {dp[i] = false;for (int j = 0; j <= i; j++) {// j == 0 时特出处理，dp[j-1] 必为 trueif ((j == 0 || dp[j-1]) && set.contains(s.substring(j, i+1))) {dp[i] = true;break;}}}return dp[n-1];}
}

3、零钱兑换 hot

题目：322. 零钱兑换 - 力扣（LeetCode）

分析：看到无限个，模仿完全背包问题。（dp[i][j] 表示挑选前 i 个物品，总重量不超过 j，所有选法中的最大总价值）

完全背包的状态转移方程：

• 状态表示：dp[i][j] 表示挑选前 i 个硬币，总金额刚好为 j，所有选法中，最少硬币个数。
• 状态转移方程：dp[i][j] = min(dp[i-1][j], dp[i][j-v[i]]+1)，j-v[i] ≥ 0。

• 初始化：dp[0][j] 选前 0 个硬币，总价值刚好为 j，做不到，应该返回 -1。但是 dp[0][j] 不能初始化为 -1，应该初始化为最大值（最大值也不能用 MAX_VLAUE，+1 时 Integer 会溢出成负数，填一个较大数就可以了 0x3f3f3f3f），因为后续计算 dp[i][j] = min(dp[i-1][j], dp[i][j-v[i]]+1) 时，会导致结果都是 -1。dp[i][0]，选前 i 个硬币，总价值刚好为 0，一个也不选，dp[i][0] 初始化为 0。
• 填表顺序：i 选前 1 个硬币到选前 n 个硬币；j 为总价值为 0 到总价值为 amount。j-v[i] < 0 时，第 i 个硬币不能选，dp[i][j] = dp[i-1][j]。
• 获取结果：选前 n 个硬币，总金额刚好为 amount，最少硬币个数，dp[n][amount]。

代码：

class Solution {public int coinChange(int[] coins, int amount) {int n = coins.length;int[][] dp = new int[n+1][amount+1];// 初始化for (int j = 1; j <= amount; j++) dp[0][j] = 0x3f3f3f3f;// 填表for (int i = 1; i <= n; i++) {for (int j = 1; j <= amount; j++) {if (j-coins[i-1] < 0) dp[i][j] = dp[i-1][j]; // 前 i 个硬币，最后一个硬币对应 coins[i-1]else dp[i][j] = Math.min(dp[i-1][j], dp[i][j-coins[i-1]]+1);}}return dp[n][amount] == 0x3f3f3f3f ? -1 : dp[n][amount];}
}

4、完全平方数 hot

题目：279. 完全平方数 - 力扣（LeetCode）

分析：完全平方数可以重复用-》完全背包。

• 状态表示：dp[i][j] 表示从 1~ i 中选择完全平方数，它们的平方和刚好为 j，完全平方数的最少数量。
• 状态转换方程：dp[i][j] = min(dp[i-1][j], dp[i][j-i^2]+1)， j-i^2 >= 0。

• 初始化：i=0 时，dp[0][j] 表示从数 0 中选，平方和刚好为 j，除了 j=0，j 为其他值都选不出来，初始化为最大值 0x3f3f3f3f（因为后续是选择较小值min，所以不能初始化为 0）。j=0时，dp[i][0] 表示从数字 1~i 中选，平方和刚好为 0，那么就不选，dp[i][0] 初始化为 0。
• 获取最终结果：dp[(int)sqrt(n)][n]。

代码：

class Solution {public int numSquares(int n) {int m = (int)Math.sqrt(n);int[][] dp = new int[m+1][n+1];// 初始化for (int j = 1; j <= n; j++) dp[0][j] = 0x3f3f3f3f;// 填表for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {int t = j-i*i;if (t < 0) dp[i][j] = dp[i-1][j];else dp[i][j] = Math.min(dp[i-1][j], dp[i][t]+1);}}return dp[m][n];}
}

5、最长递增子序列 hot

        注：子数组指的连续序列（n^2 级别）。子序列的元素可在原数组中不连续，但相对位置不能改变（2^n级别）。

题目：300. 最长递增子序列 - 力扣（LeetCode）

分析：

• 状态表示：dp[i] 表示以 i 为结尾的所有子序列中的最大长度。
• 状态转移方程：dp[i] = max(1, dp[j] + 1)，dp[j] = max(dp[0], dp[2],……, dp[i-1])

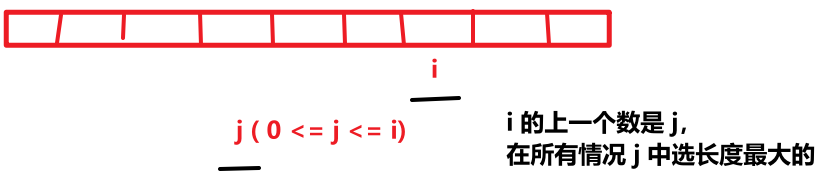
• 初始化：因为有遍历 j=i-1 的情况，i = 0 时我们单独处理。若 i = 0，dp[0] = 1，子序列就是第一个数，后续 i 就从 1 开始填表。
• 最终结果：dp 数组中的最大值。

代码：

class Solution {public int lengthOfLIS(int[] nums) {int n = nums.length;int[] dp = new int[n];dp[0] = 1;int ret = dp[0];for (int i = 1; i < n; i++) { for (int j = 0; j < i; j++) {if (nums[j] < nums[i]) dp[i] = Math.max(dp[i], dp[j]);}dp[i] = Math.max(1, dp[i]+1);ret = Math.max(ret, dp[i]);}return ret;}
}

6、乘积最大子数组 hot

题目：152. 乘积最大子数组 - 力扣（LeetCode）

分析：

• 状态表示：dp[i] 表示以 i 结尾的所有子数组中，乘积最大的子数组的乘积。
• 状态转换方程：

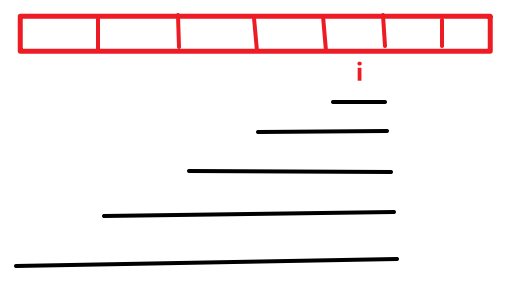
所以要维护两个dp，一个存最大乘积，一个存最小乘积。

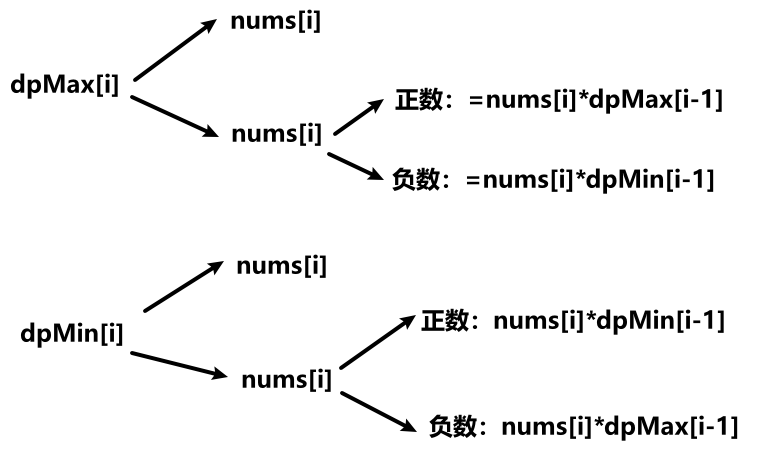
• 初始化：i=0 时会越界，单独处理 i=0，dp[0]=nums[i]。然后从左往右填表。
• 最终结果：两个 dp 里面的最大值。

代码：

class Solution {public int maxProduct(int[] nums) {int n = nums.length;int[] dpMax = new int[n], dpMin = new int[n];// 初始化dpMax[0] = nums[0];dpMin[0] = nums[0];int ret = dpMax[0];// 填表for (int i = 1; i < n; i++) {if (nums[i] >= 0) {dpMax[i] = Math.max(nums[i], dpMax[i-1]*nums[i]); // 最大乘积dpMin[i] = Math.min(nums[i], dpMin[i-1]*nums[i]); // 最小乘积}else {dpMax[i] = Math.max(nums[i], dpMin[i-1]*nums[i]);dpMin[i] = Math.min(nums[i], dpMax[i-1]*nums[i]);}ret = Math.max(ret, dpMax[i]);ret = Math.max(ret, dpMin[i]);}return ret;}
}