Huffman树的实现

$Huffman$树的实现

一、前言

前面我们学过了二叉树的各种形态，今天我将带来一种更为高效的树。它的出现，就是为了解决一个核心问题：如何用最短的二进制编码来表示信息，从而最大限度地节省空间或传输带宽。到底是怎样的原理呢？我将对此进行一个深入解读。

二、哈夫曼树相关的概念

2.1 路径

在一棵树中，一个节点到另一个节点之间的通路，称为路径。

和生活中的路径很相似，只是把建筑物换成了节点。

2.2 路径长度

在一条路径中，每经过一个节点，路径长度+1。（路径长度就是经过的节点数）

在一棵树中，规定根节点所在的层数是第一层。

2.3 节点的权

权，其实就是一个数值。每个节点被赋予一个值，被称为节点的权。这里的节点指的是叶子节点。

2.4 节点的带权路径长度

该节点的权重×根节点到节点的路径长度。

树中所有叶子节点的带权路径长度之和，通常记作“$WPL$​”

上图展示一下更为清晰~
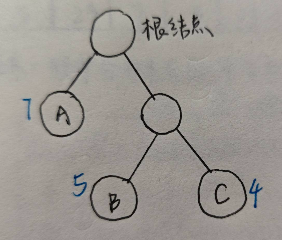
如图：

在上图中A节点的路径长度为1，B节点的路径长度为2，C节点的路径长度为2。
A节点的权值是7，B节点的权值是5，C节点的权值是4。
A的带权路径长度为：7 × 1 = 7；B的带权路径长度为：5 × 2 = 10
$WPL$：7 × 1 + 5 × 2 + 4 × 2 = 25

三、哈夫曼树（$Huffman$ 树）

3.1 概述

当用n个节点构建一棵树，经过合理的排列，如果构建的这棵树的带权路径长度（$WPL$​）最短，这棵树被称为“最优二叉树”，有时也叫“赫尔曼树”或“哈夫曼树”。

哈夫曼树的基本思想是贪心算法。

什么是贪心算法呢？
贪心算法就是模拟贪心的人做出决策的过程。只考虑眼前的最优操作（只考虑局部最优），并不考虑以后可能会造成的影响。贪心算法主要用于解决最优解问题。

相信你已经明白它的主要目的了吧~
就是让权值大的节点的路径尽可能短，也就是尽可能地靠近根节点。

3.2 应用场景

• 哈夫曼编码。

  对数据：$AAABBACCCDEEA$，设计编码，使其传输效率较高，比如压缩一下。

  等长编码：
  统计：
  $A：5$
  $B：2$
  $C：3$
  $D：1$
  $E：2$
  3$bit$编码：000 001 010 011 100 101 110 111
  在3$bit$编码中任意选择5个状态赋给$ABCDE$
  结果：13个符号 * 3$bit$ = 39$bit$
  缺点：所占空间过大
  改进：可以采用变长编码，根据统计的出现频率大小，采用不同的编码方式。比如：A：采用1$bit$，C采用2$bit$，B采用3$bit$，E采用2$bit$，D采用5$bit$
  缺点：这种编码属于前缀码，接收端没法接收（前缀重复，导致无法解析）

  最优解：哈夫曼编码（贪心算法)。

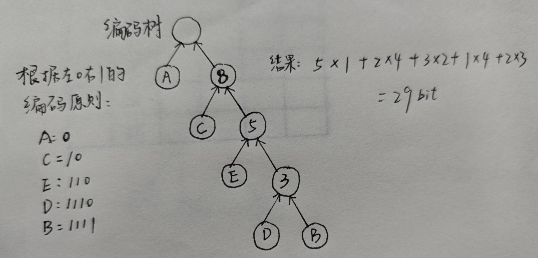
  如图：

  

  重复类似这样的操作，最终形成：

  

• 文件压缩。

• 网络通信：压缩待传输的数据，减少网络宽带的占用。

3.3 实现

由于根节点是动态生成的（最后才形成），实现起来比较困难。

性质：n个子节点，$Huffman$树的总节点个数：$2n-1$

$n0=n2+1$（在树的基本概述中已有所阐述）
$n0+n1+n2=n+0+n-1$
n0：所有本来就有的节点都是叶子节点
n2：构建而成的点都是度为2的节点
如图：

3.3.1 实现树

思路：

• 树的表示就是要把节点之间的关系表示清楚。
• 节点就是叶子节点，总节点数已经确定了。节点可以直接用索引号来存，所以直接用顺序存储即可，只存下标（节点索引从1开始，0号索引当作一个“非法节点”，用来表示根节点）。实现一个总节点的映射表的形式。

如图：

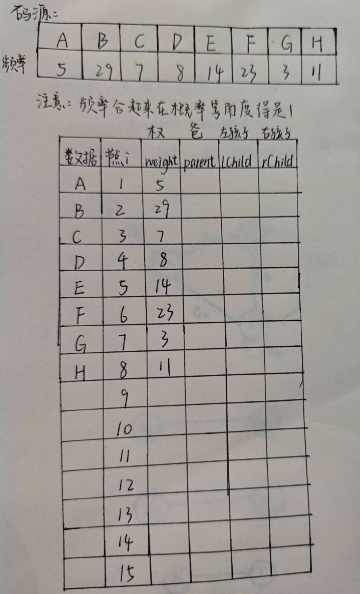
申请16个空间（0号节点不用），最开始每个节点的左孩子，右孩子，爸为0（不存在）。最后，每个叶节点都有爸，只有根节点的爸是0。

哈夫曼树的构建，就是将这个表后面的空填完。

步骤：

• 定义树结构，申请空间
• 初始化
• 填充 n + 1下标到m下标的空间，构建哈夫曼树
  如图：

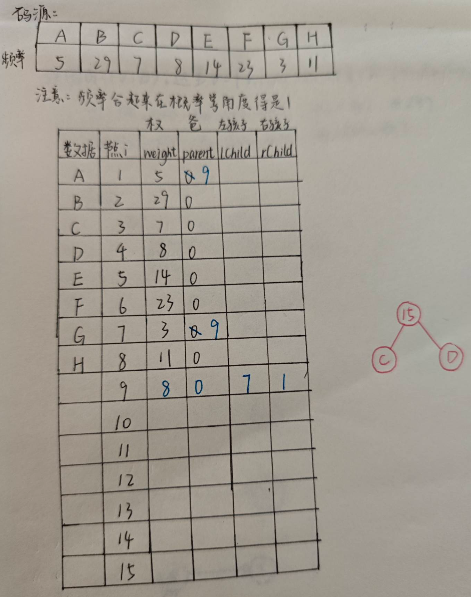
填完之后如下图：

// 定义Huffman树的节点结构(也是头结构)，采用顺序存储方式。通过下标索引来标识不同的节点
typedef struct
{int weight;int parent;int lChild;int rChild;
} HuffmanNode, *HuffmanTree;// 头指针// *s1最小值，*s2次小值
static void selectNode(HuffmanTree tree, int n, int *s1, int *s2)
{// 先假设一个最小值int mini = 0;// 找到第一个父节点为0的编号，把它当作最小值for(int i = 1; i <= n; ++i){if(tree[i].parent == 0){mini = i;break;}}for(int i = 2; i <= n; ++i){if(tree[i].parent == 0 && tree[i].weight < tree[mini].weight){mini = i;}}*s1 = mini;// 开始找第二个最小权值的点for(int i = 1; i <= n; ++i){if(tree[i].parent == 0 && i != *s1){mini = i;break;}}for(int i = 1; i <= n; ++i){if(tree[i].parent == 0 && i != *s1){if(tree[i].weight < tree[mini].weight){mini = i;}}}
}// 已知n个字符的权值表，创建HuffmanTree
HuffmanTree createHuffmanTree(const int *w, int n)
{// 定义指针HuffmanTree tree;// 总共的节点数，决定了申请多大的空间int m = 2 * n - 1;// 1.1 申请2n个单元，从1号索引开始存储数据tree = malloc(sizeof(HuffmanNode) * (m + 1));if(tree == NULL){return NULL;}// 初始化1 ~ 2n - 1个节点for(int i = 1; i <= m; ++i){tree[i].parent = tree[i].lChild = tree[i].rChild = 0;tree[i].weight = 0;}// 1.2 设置初始化的权值for(int i = 0; i < n; ++i){tree[i].weight = w[i];}// 填充 n + 1下标到m下标的空间int s1,s2;for(int i = n + 1; i <= m; ++i){// 在[1...i-1]范围内，父节点为0，权值最小的两个点selectNode(tree, i - 1, &s1, &s2);// 将这两个权值最小的节点，组合到第i个位置上（父节点）tree[s1].parent = tree[s2].parent = i;tree[i].lChild = s1;tree[i].rChild = s2;tree[i].weight = tree[s1].weight + tree[s2].weight;}// 返回指针return tree;
}

3.3.2 $Huffman$编码

思路：上文中$Huffman$树已经构建完成，在$Huffman$编码中，每个节点对应一串编码。因此可以生成一个编码表。通过遍历$Huffman$树生成对应的编码。

如图：

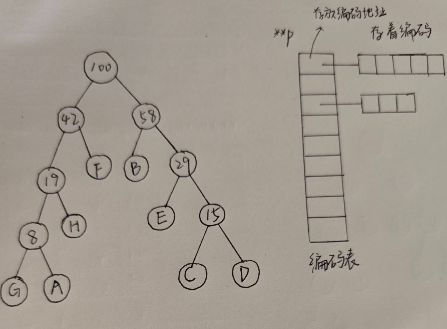
步骤：

• 定义编码表
• 申请编码空间
• 遍历$Huffman$树（字符），生成$Huffman$编码

// Huffman编码指针，表示Huffman是指向char的指针
typedef char *HuffmanCode;
// 依据Huffman树，产生n个Huffman编码
HuffmanCode *createHuffmanCode(HuffmanTree tree, int n)
{// 生成n个字符的编码表，每个表项里保存编码的空间首地址，codes是指编码表dHuffmanCode *codes = malloc(sizeof(HuffmanCode) * n);if (codes == NULL){return NULL;}// 空间清零memset(codes, 0, sizeof(HuffmanCode) * n);// 每求一个字符时，倒序构建，n个节点，树的高度最高是n，编码个数最多为nchar *temp = malloc(sizeof(char) * n);	// 临时字符数组int start;              // temp空间的起始位置int p;                  // 存放当前节点的父结点信息int pos;                // 当前编码的位置// 逐个字符求Huffman编码for (int i = 1; i <= n; ++i){// 从后往前填start = n - 1;// 规定结束标志temp[start] = '\0';pos = i;p = tree[i].parent;while (p){--start;temp[start] = (tree[p].lCh2ild == pos) ? '0' : '1';pos = p;// 下一个p = tree[p].parent;}// 第i个字符编码分配的空间codes[i - 1] = malloc(sizeof(HuffmanCode) * (n - start));strcpy(codes[i - 1], &temp[start]);}free(temp);return codes;
}

为什么遍历$Huffman$树生成的编码是倒序的？

在生成$Huffman$树时，生成节点的过程是从下往上生成的，根节点最后才确定。因而遍历时也是倒序的，需要最后再修正一下顺序。

3.3.3 释放$Huffman$树

easy~

void releaseHuffmanCode(HuffmanCode* codes, int n)
{if (codes){for (int i = 0; i < n; ++i){if (codes[i]){free(codes[i]);}}}
}

3.4 优缺点辨析

3.4.1 优点

• 最优压缩效率：在已知频率的情况下，能产生$WPL$最短的编码，实现最高压缩率，并且不会损失原始信息。
• 前缀无歧义：产生的哈夫曼编码是前缀码，任何字符的编码都不会是另一个字符编码的前缀。（哈夫曼树的唯一性，根节点到叶子节点的路径是唯一的）

3.4.2 缺点

• 依赖静态统计：需要预先扫描全部数据已统计字符效率，不适合实时数据流或频率动态变化的场景。

  从哈夫曼树的实现可知，节点的权值是预设的。

• 编码表带来的空间开销

• 对数据分布敏感：当字符出现频率接近均匀分布时，压缩效果会大打折扣。

四、小结

树结构的探索永无止境，但目前先告一段落了~下一篇将开启图结构的学习。

关于高级树结构（红黑树，B树，B+树），后续会补上哒~